les thèmes abordés dans cette page
repérage sur un axe et milieux de segments
(6ème)
conservation des longueurs par symétrie
centrale
(5ème)
opérations sur les unités de temps et
d'angle
(6ème et 5ème)
triangle rectangle et parallélogramme
(4ème)
équation du premier degré à une inconnue
(4ème)
existence et signe des racines
d'une équation
du second degré
(seconde)
le raisonnement par récurrence
(premières et
terminales)
combinaisons et probabilités
(terminale L)
maximum d'une quantité,
fonction de deux
variables réelles positives et indépendantes
(terminale L)
tétraèdre et plans parallèles
(1ère S)
équation du second degré et probabilités
(premières, toutes séries confondues)
polynômes et
primitives
(terminales scientifiques toutes séries confondues)
nombres complexes et transformations
géométriques
(terminales scientifiques toutes séries
confondues)
les nombres
décimaux
(groupe ciblé : sixième)
1- On te donne les deux nombres décimaux suivants :
8759,5056 ; 125076,8051
Quelles sont leurs parties entières respectives
?
Parmi eux lequel a le chiffre des centaines égal à celui des centièmes ?
Parmi eux lequel a le chiffre des dizaines égal à celui des dixièmes ?
2- On te donne les 7 nombres suivants :
4,05 ; 12,67 ; 04,0500 ; 004,050 ; 12,670 ; 12,067 ; 012,6700 .
Classe les par ordre croissant en utilisant les symboles = et < .
3- Trouve le nombre décimal @ @ @,@ @ vérifiant les propriétés suivantes :
a) le chiffre des centaines est le double de
celui des dizaines ;
b) le chiffre des dizaines est identique au chiffre de unités ;
c) le chiffre des unités vaut 3 de plus que celui des dixièmes ;
d) le chiffre des dixièmes vaut 4 de moins que celui des centièmes ;
e) le chiffre des centièmes est égal à 5 .
NB :
Pour répondre à la question n° 2, tu dois te rappeler que dans l'écriture
d'un nombre décimal, parfois des zéros sont superflus et donc inutiles.
Pour répondre à la question n° 3, tu dois dans un premier temps lire
attentivement tout le texte, puis ensuite commencer par la fin.
droite graduée
(groupe ciblé : sixième)
Dessine sur ta feuille une droite graduée en prenant pour unité de mesure des longueurs, le centimètre.
Marque sur cette droite les points A, B, C et D après avoir attentivement lu le passage suivant : "
- l'abscisse du point A
est le double de celle de B
- l'abscisse du point C est la moitié de celle de D
- l'abscisse de B est égale à celle de C diminuée de 3
- l'abscisse de D est 10 "
milieux de segments
(groupe ciblé : sixième)
A l'aide de ton compas, place sur une droite d
deux points distincts quelconques A et B.
Place le point C tel que A soit milieu de [CB].
Place le point D tel que B soit le milieu de [AD].
Complète la phrase suivante :" |CD| ..... |AB| ".
Je te rappelle que la longueur ou la mesure
géométrique d'un segment [AB] se note |AB| .
Trace une droite graduée l dont l'unité de mesure des longueurs sera le
centimètre.
Place sur cette droite les points M d'abscisse xM = +2,5 et N
d'abscisse xN = +3,5.
Avec ton compas , place le milieu P de [MN].
Qu'observes - tu ? Complète la phrase suivante : "( xM + xN ) est égale ..... xP ".
Prends deux autres points de ton choix, R
et S sur l.
Observe que la phrase complétée ci-dessus reste vraie pour R et S.
symétrie axiale
(groupe ciblé : sixième)
Trace sur ta feuille une droite D et trois points
A, B, C et O tels que les trois premiers n'appartiennent
pas à D et O
appartient à D.
Construis le segment [AA'] sachant que A' est le
symétrique de A dans la symétrie axiale d'axe D.
Construis le triangle (BOB') sachant que B' est le symétrique de B dans la
même symétrie.
Construis le symétrique du triangle (ABC) dans la même symétrie.
Construis le triangle équilatéral (BEF) sachant que D est l'un de ses axes de
symétrie.
conservation des longueurs par symétrie
centrale
(groupe ciblé : cinquième)
Construis le triangle (ABC) rectangle en A et tel
que |AC| = 3 cm et |AB| = 1 cm.
Construis B' et C' les symétriques de B, C par rapport au point A.
Montre que
|BC| est égale à |B'C'|.
Quelle est la nature du quadrilatère (BCB'C') ?
lumière et son
(groupe ciblé : cinquième)
1-
La lumière du Soleil met environ 8min 18s pour parvenir à la Terre.
La
distance entre la Terre et le Soleil est de 149 400 000 km.
Quelle distance parcourt la lumière en une seconde ?
2-
La vitesse du son est environ 331 mètres par seconde.
Tu te trouves devant un puits et tu souhaites, sans prendre le risque de le pénétrer,
connaître sa profondeur.
Muni
d’une montre te permettant de chronométrer, comment procèderas-tu et quels
sont les
calculs que tu feras ?
fractions
(groupe ciblé : cinquième)
1- Complète les égalités suivantes :
![]()
2-
Écris les nombres suivants sous forme de fraction :
0,04 ; 0,7 ; 0,75 ; 50,25
3- Simplifie les fractions suivantes :
![]()
4- Compare les fractions suivantes ( tu utiliseras les symboles < et > ) :
![]()
5-
Dans une classe de 18 élèves , deux tiers des élèves ont eu la moyenne et un
sixième ont eu moins de 4.
Combien d'élèves ont eu la moyenne ?
Combien d'élèves ont eu moins de 4 ? entre 4 et 10 ?
opérations sur les unités de temps et
d'angle
(groupes ciblés : sixième et cinquième)
Les règles qui s'appliquent lors des opérations sur les unités de temps s'appliquent également aux opérations portant sur les mesures des angles.
Ainsi 3° 12' 20'' + 15° 53' 43'' donne 18° 65'
63''.
63" = 60" + 3" ; donc 63" valent 1' 3".
La première
partie de la réponse est 3" ; 1' est ajoutée à 65', le résultat est
66'.
66' = 60' + 6' ; donc 66' valent 1° 6'. La seconde partie de ta réponse est
6' ; 1° est ajouté à 18°.
La réponse finale est donc 19° 6' 3".
Prends la soustraction suivante :
15° 5' 3" - 7° 10' 15"
Tu constates que les soustractions partielles 5' - 10' et 3" - 15"
sont impossibles.
Pour lever cette impossibilité, il te faudra extraire 1° des 15°, le
convertir en minutes d'angle et ajouter le résultat à 5' ; tu obtiens donc 60'
+ 5' = 65'.
Ainsi et provisoirement tu as 15° 5' 3" = 14° 65' 3".
Maintenant tu extrais 1' de 65' que tu convertis en secondes d'angle et que tu
ajoutes à 3" ; tu obtiens donc 60" + 3" = 63" et
65' 3" = 64' 63".
Finalement 15° 5' 3" = 14° 64' 63".
La soustraction 15° 5' 3" - 7° 10' 15" devient 14° 64' 63" - 7° 10' 15" et la réponse finale est 7° 54' 48".
Effectue toi-même les opérations suivantes :
12° 20' 15" × 7 ; 65° 23' 36" ÷ 2.
Peux-tu dire pourquoi la soustraction 5° 13'
45" - 5° 13' 46" est impossible ?
Calcule 7° 13' 2" - 6° 15' 13".
Effectue les opérations suivantes :
7h 53mn 12s ÷ 3
3° 23' 15" + 1° 54' 59"
8° 2' 1" - 6° 13' 21"
échelle d'une carte
(groupe ciblé : cinquième)
Deux villes sur une carte routière sont
distantes à vol d'oiseau de 760 km.
Calcule leur distance réduite en centimètre sachant que l'échelle de la carte
est :
![]()
Sur une seconde carte routière, deux autres villes ont une distance réduite égale à 20,5 cm.
L'échelle de cette carte est :
![]()
Calcule la
distance de ces deux villes à vol d'oiseau.
triangle rectangle et parallélogramme
(groupe ciblé : quatrième)
On te donne un triangle (ABC), rectangle en A.
|AB| = 5 cm ; |AC| = 6 cm.
E est le milieu de [AC]. I est le centre du cercle circonscrit au triangle
(ABC).
Démontre que les droites (EI) et (AB) sont parallèles.
Construis le triangle (MNP), rectangle en M et
tel que |MN| = 7,2 cm et |MP| = 4,8 cm.
Prends F milieu de [MN]. Calcule |PF|.
Prends K milieu de [PF]. Calcule |MK|.
La parallèle à (MK) passant par F coupe (MP) en J.
Montre que M est milieu
de [PJ]. Détermine |JF|.
On te donne un quadrilatère quelconque (KLMN).
Prends A, B, C et D les milieux respectifs de [KL], [LM], [MN] et [NK].
Démontre que le quadrilatère (ABCD) est un parallélogramme.
cosinus d'un angle
(groupe ciblé : quatrième)
1-
A l'aide de ta calculatrice donne une valeur
approchée au millième près des nombres suivants :
cos 43° ; cos 60° ; cos 1° ; cos 45° ; cos 20°.
2-
On te donne cos a = 1/3 ; a étant la mesure en degré du secteur
angulaire aigu A.
Détermine une valeur approchée à 1° près de a.
3- (MNP) est un triangle rectangle en M.
|NP| = 6 cm et mes ([NM ; [NP) = 55°.
Construis (MNP).
Détermine mes ([PM ; [PN).
Calcule une valeur approchée de |MN| et |MP|.
calcul littéral
(groupe ciblé : quatrième)
1- Développe et réduis les expressions
suivantes :
M = -2(2x+1)+(x-1)(x-3)
N = 2(x-11)-5(2-4x)+x2 -5
2 - Développe et réduis l'expression suivante :
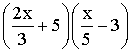
3- On te donne un carré (ABCD) et un rectangle (BEFC), l'un et l'autre de part et d'autre de (BC).
La mesure du côté du carré est x cm et |BE| = 3 cm.
P est la mesure du périmètre de l'objet géométrique défini par ce carré et
ce rectangle.
S est la mesure de son aire.
Exprime P en fonction de x et calcule p pour x = 4 cm et pour
![]()
Exprime S en fonction de x et calcule S pour x = 2,5 cm et pour
![]()
puissance ou exposant d'un
nombre
(groupe ciblé : quatrième)
1- Calcule les nombres suivants :
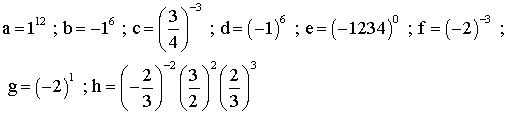
2- Écris sous la forme d'une seule puissance :
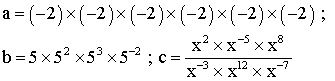
3- Calcule :

4-
L'Année Lumière est la distance parcourue par la lumière dans le vide en une
année.
Calcule cette distance en km sachant que la vitesse
de la lumière dans le vide est égale à 300000 km.s-1.
La distance de la Terre à la Lune est de 3,84.105 km.
Exprime cette
distance en année lumière (AL).
La plus proche étoile de la Terre est à environ 4,5 AL ; exprime cette
distance en kilomètres.
résolution d'une équation du 1er degré à
une inconnue
(groupe ciblé : quatrième)
1- Résous les équations suivantes :
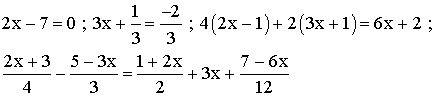
2- On te donne la figure suivante :
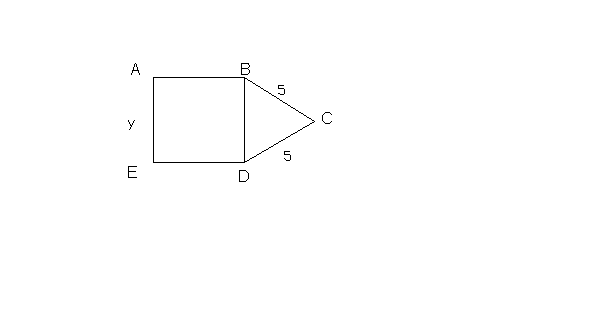
Le
périmètre du carré (ABDE) est égal à celui du triangle (BCD).
Quelle est la mesure y du côté du carré ?
( unité de mesure des longueurs : mètre )
application
affine
(groupe ciblé : troisième)
1-
Trouve l'application affine f sachant que f(1) = 2 et f(3) = -1.
2-
Trouve le nombre y ayant même image par g et h sachant que :
g(x) = x + 5 et h(x) = -2x -1
Détermine l'équation de la droite D passant par M(1;3) et perpendiculaire à
la courbe représentative de h.
étude de l'existence et du signe des
racines d'une équation du second degré
(groupe ciblé : seconde)
Soit l'équation (m-1)x2 + mx -1 = 0 , m réel différent de 1.
Étudie, en fonction du paramètre m, l'existence et le signe des racines
réelles de cette équation.
Tu présenteras les résultats de cette étude dans
un tableau.
Étudie graphiquement, et en fonction du
paramètre réel m, l'existence des racines
réelles de
l'équation x2 - m -1 = 0.
Pour quelles valeurs du paramètre réel n différent de 0, les racines réelles de l'équation :
nx2 - (n - 1)x + 1 = 0,
existent-elles et sont :
toutes deux négatives ?
toutes deux positives ?
de signes
contraires ?
le raisonnement par récurrence
(groupes ciblés : premières et terminales)
A - Soit N l'ensemble des entiers naturels.
Soit E un ensemble quelconque d'objets mathématiques.
On dira que E est numéroté au moyen des
éléments de N, lorsque tout élément de E porte
un numéro et un seul
appartenant à N.
Dans ce cas, il est possible d'utiliser sur cet ensemble E le raisonnement par
récurrence qui consiste à :
- vérifier qu'une propriété ( P ) est vérifiée pour l'élément portant le numéro n0 ;
- démontrer que l'hypothèse " ( P ) est vérifiée pour un élément portant le numéro n tel que n est supérieur ou égal à n0 " implique logiquement " ( P ) est vérifiée pour l'élément portant le numéro ( n + 1 ) ".
Dès lors la propriété P est vérifiée pour tout élément portant un numéro au moins égal à n0.
B - Montre par récurrence que, pour tout n
entier supérieur ou égal à 3, 2n2 > (n + 1)2 et que,
pour tout n supérieur ou égal à 5 , 2n > n2.
C - On désigne par Sn la somme 1 + 3
+ 5 + ...+ (2n - 1) des premiers entiers naturels impairs.
Calcule Sk, k parcourant l'ensemble {1 , 2 , 3 , 4 , 5} et observe
que toutes ces sommes sont des carrés parfaits.
Trouve en utilisant le
raisonnement par récurrence l'expression de Sn en fonction de n.
D - On te donne trois variables réelles x, y et z liées par la relation x + y + z = 0.
Pose xy + yz + xz = S
et xyz = P.
Désigne
par Sn la somme xn + yn + zn.
- Calcule en fonction de P et de S les sommes S2 et S3
- Établis une formule de récurrence entre Sn , Sn-2 et Sn-3
- En utilisant cette formule de récurrence , calcule en fonction de P et de S
les sommes S4 , S5 , S6 et S7- Vérifie les égalités : 2S4 = S22 ; 6S5 = 5S2S3 et 10S7 = 7S2S5
- Trouve les valeurs de P et de S pour que S3 = 18 et S6 = 794
Calcule x , y et z
1- Sur dix familles de ton
entourage, sept ont une voiture, six ont un téléphone, trois ont un
ordinateur,
trois ont une voiture et un ordinateur, cinq ont une voiture et un
téléphone, deux ont un téléphone et
un ordinateur et deux ont une voiture,
un téléphone et un ordinateur.
Combien de familles n'ont aucun de ces objets ?
Combien de familles ont seulement une voiture ?
combien de familles ont seulement un téléphone ?
2- Tu tires deux cartes dans un jeu de 32 cartes.
Trouves la probabilité d'avoir un roi ou une dame.
maximum d'une quantité , fonction de deux
variables réelles positives et indépendantes
(groupe ciblé : terminale L)
Trouve le maximum de la quantité U = x+y ; x et
y étant deux variables réelles, positives
et indépendantes, vérifiant les
conditions suivantes :
![]()
tétraèdre et plans parallèles
(groupe ciblé : première S)
On te donne un tétraèdre (ABCD) dans lequel les
arêtes [AB] et [CD] sont orthogonales.
Soient I et J les milieux respectifs de
[AB] et [CD].
Un plan variable S, parallèle à (AB) et (CD) coupe (IJ) en O et les arêtes
[BC], [BD], [AD], [AC] respectivement en M, N, P, Q.
Montre que (MNPQ) est un rectangle.
Montre que les diagonales de ce rectangle se coupent en un point de (IJ).
Calcule l'aire de (MNPQ) en fonction de mes [AB] = a, mes [CD] = b, mes [IJ] =
c et mes [IO] = x.
Détermine x pour que cette aire soit maximum et calcule ce maximum.
équation du second degré et probabilités
(groupe ciblés : premières toutes séries
confondues)
On te donne l'équation x2 + mx + n =
0 ; x est l'inconnue.
Le coefficient m est obtenu en jetant un dé rouge et n , en jetant un dé noir.
Quelle est la probabilité pour que cette équation ait deux racines réelles
distinctes ?
une racine double ?
Prends l'expression E(x) = x2 + mx + n.
Quelle est la probabilité pour que E(x) soit strictement positive quelle que
soit la valeur de x ?
polynômes et primitives
(groupes ciblés : terminales scientifiques toutes
séries confondues)
On te donne le polynôme P(x) = x3 +
mx2 + nx dans lequel m et n sont deux constantes
réelles quelconques.
1) Calcule, sans effectuer la division, le
reste R de la division de P(x) par (x - 1).
2) Tu désigneras par Q(x) le polynôme
vérifiant :
P(x) = (x - 1).Q(x) + R et par Q'(x) la dérivée de Q(x).
a) Détermine n en fonction de m pour que la fonction :
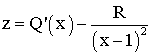 s'annule lorsque x = -1.
s'annule lorsque x = -1.
b) Étudie alors, en fonction de m, le nombre des racines de l'équation z = 0.
c) Calcule t, a, b, m pour que z puisse se mettre sous la forme :
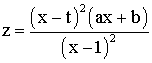
3) L'une des trois fonctions z que l'on vient
d'obtenir s'annule pour x = 2.
Tu désigneras par z1 (x) cette
fonction et par y1 (x) celle des primitives de z1 qui
s'annule pour
x = 0.
a) Trouve en utilisant l'expression donnée en (2-a) la fonction y1 (x)
= F(x).
b) Étudie les variations de la fonction y1
(x) = F(x) et trace sa courbe représentative (C) dans
un
système d'axes rectangulaires x'Ox et y'Oy dans lesquels tu prendras pour
unités 1 cm sur l'axe
x'Ox et 0,5 cm sur l'axe y'Oy.
Trace dans ce même système la courbe (C') d'équation :
![]()
Calcule l'aire de la portion de plan comprise entre (C) ; (C') et les droites d'équations x = 2 et x = 3.
nombres complexes et transformations
géométriques
(groupes ciblés : terminales scientifiques et
technologiques)
On identifie le plan complexe à R2.
On donne dans ce plan la fonction f(z) = Z = az, avec a nombre complexe non nul.
r et g étant respectivement le module et l'argument de z, nous noterons z = (r
;g).
Il en est de même pour a : a = (l
; a).
Étudie la transformation géométrique Tf qui en découle selon que a est réel pur ou imaginaire pur.
On suppose pour la suite que
![]()
Dans un repère orthonormé défini dans le plan R2, on considère la parabole (P) d'équation cartésienne
y = x2.
Trouve l'équation cartésienne de Tf (P) qu'on nommera (P').
Calcule les coordonnées du point M : intersection de (P) et (P').
On donne l'ensemble :
![]()
Écris l'équation de G.
Montre que G admet un axe de symétrie dont on écrira son
équation.