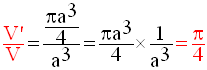L'ATELIER DU COLLÉGIEN
(page 2)
(groupes ciblés : de la sixième à la
troisième)
les thèmes abordés dans cette page
la
résolution d'une équation
(6ème)
fractions et opérations sur les fractions
(5ème, 4ème et 3ème)
la
résolution d'une équation
(groupe ciblé : sixième)
Une équation est
une égalité dans laquelle figure un nombre inconnu
ou une quantité inconnue.
Une équation est donc composée de deux membres
séparés par le signe de l'égalité =
Le membre situé à gauche du symbole = est souvent appelé premier
membre de l'équation; celui de droite est appelé second
membre.
La quantité inconnue peut figurer soit dans le premier membre, soit dans le
second, soit dans les deux.
Résoudre une équation veut dire trouver par le calcul la ou les valeurs que peut prendre la quantité inconnue; ces valeurs sont également appelées racines ou solutions de l'équation.
Dans une équation, le nombre inconnu peut être représenté
par un objet quelconque : un petit symbole ou encore une lettre.
Souvent cet inconnu est représenté par la lettre x.
Mettre en équation l'énoncé d'un problème veut dire traduire les hypothèses et la question du problème en équation.
Méthode de résolution d'une équation
1- Si j'ajoute une même
quantité aux deux membres d'une
équation, j'obtiens encore une équation.
Exemple :
Soit à résoudre l'équation x - a = b, l'inconnu étant x.
Je remarque qu'en ajoutant a au premier membre, donc x - a + a, j'obtiens x, car
- a + a = 0.
Dans ce cas il faudra également ajouter a au second membre, et j'obtiens donc b
+ a.
Ainsi x - a = b implique que x - a + a = b + a ou x = b + a.
La solution de l'équation est donc la valeur b + a.
2- Si je retranche une même
quantité des deux
membres d'une équation, j'obtiens encore une équation.
Exemple :
Soit l'équation x + m = n, l'inconnu étant x et .
Je remarque qu'en retranchant m des deux membres, j'obtiens la valeur de l'inconnu x.
En effet, x + m - m = n - m
Mais m - m = 0
Donc x = n - m
La solution de l'équation est donc la valeur n - m.
3- Si je multiplie ou je divise par une même quantité différente de 0 les deux membres d'une équation, j'obtiens encore une équation.
Exemple 1
Soit l'équation a × y = d où le nombre inconnu est y et a différent de 0.
Si je divise les deux membres de cette équation
par a, j'obtiens encore une équation et ainsi :
![]()
![]()
![]()
Exemple 2
![]()
Si je multiplie les deux membres de cette
équation par c, j'obtiens encore une équation et ainsi :
![]()
![]()
L'équation
devient :
![]()
4- Conclusion générale
Si par une même transformation T, je transforme les deux membres d'une équation, j'obtiens encore une équation.
Exemple :
![]()
La
transformation T à utiliser est la suivante : «
J'ajoute b aux deux membres, puis je multiplie par a les deux membres de la
nouvelle équation obtenue »
En ajoutant b aux deux membres de cette équation, on obtient :
![]()
En multipliant les deux membres de cette dernière équation par a, on obtient :
![]()
Applications
1ère application
Trouve les nombres manquants dans les cases suivantes :
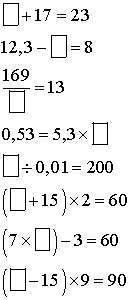
2ème application
Muhammad AL-KHAWARIZMI (780 env. - 850 env.) était un mathématicien arabe.
On te donne l’extrait de dialogue suivant : «
AL-KHAWARIZMI : Pense à un nombe
Raymond : C’est fait
AL-KHAWARIZMI : Ajoute lui 12
Raymond : C’est fait
AL-KHAWARIZMI : Multiplie le résultat par 3
Raymond : C’est fait
AL-KHAWARIZMI : Donne moi la réponse finale
Raymond : 51
AL-KHAWARIZMI : Le nombre auquel tu as pensé est 5 ».
Explique comment AL-KHAWARIZMI a-t-il procédé pour deviner le nombre pensé par Raymond.
3ème
application
Un
rectangle mesure 27 cm de longueur et 80 cm de périmètre.
Combien mesure la largeur ?
4ème
application
Peux-tu trouver dans combien d'années l'âge de ton père sera-t-il le double du tien ?
fractions et opérations sur les fractions
(groupes ciblés : cinquième, quatrième et
troisième)
De la cinquième à la troisième
A- Généralités
A1- Définitions
On donne deux nombres entiers naturels a et b, avec b différent de 0.

A2- Invariance
de la fraction et égalité de deux fractions
On ne change pas une fraction si on multiplie ou on divise son numérateur et son dénominateur par un même nombre différent de 0.

De
cette propriété se déduit donc l'égalité de
deux fractions.

Exemples
:
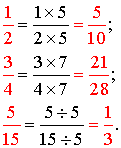
A3- Comparaison de fractions; ordre
De deux fractions de même dénominateur, la plus grande est celle qui possède le plus grand numérateur.
De deux fractions de même numérateur, la plus grande est celle qui possède le plus petit dénominateur.
Soit
a un nombre entier différent de 0 et quelconque.
On dira qu'un nombre entier b est un multiple de a si
et seulement s'il
![]()
Dans ce cas on dit également que a divise b ou
encore que a est un diviseur
de b.
Exemples :
8 est multiple de 4 car 8 = 2 × 4;
51 est multiple de 17 car 51 = 3 × 17.
0
est multiple de 9 car 0 = 0 × 9
Pour
comparer des fractions ayant des dénominateurs différents, il faut
d'abord les réduire au même dénominateur;
c'est-à-dire il faut trouver des fractions qui leur sont respectivement
égales et qui ont toutes le même dénominateur. Ce
dernier est un multiple commun à tous les
dénominateurs différents.
Exemples de comparaison de fractions :
![]()
Les dénominateurs différents sont 2, 4 et 8.
Un
multiple commun à ces dénominateurs est, par exemple, 8.
En effet 8 = 4 × 2 = 2 × 4.
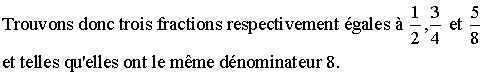
On ne change pas une fraction si on multiplie son numérateur et son dénominateur par un même nombre différent de 0.
Donc on a respectivement :
![]()
![]()
![]()
Les dénominateurs différents sont 3, 5 et 7. Un multiple commun de 3, 5 et 7
est 3 × 5 × 7 = 105.

On ne change pas une fraction si on multiplie son numérateur et son dénominateur par un même nombre différent de 0.
Donc on a respectivement :
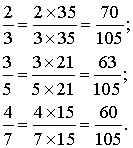
![]()
A4- Applications
1ère application
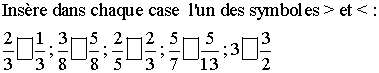
2ème application

3ème application
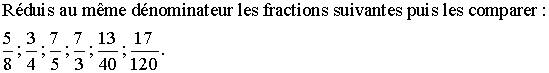
A5- Simplification d'une fraction
Simplifier une fraction consiste à trouver une fraction qui lui soit égale et dont le numérateur et le dénominateur sont deux nombres ayant 1et seulement 1 comme diviseur commun.
Pour
simplifier une fraction, il suffit de diviser son numérateur et son
dénominateur par un même nombre différent de 0. Généralement ce
nombre est un diviseur commun du numérateur et du dénominateur.
Ce procédé devra se poursuivre jusqu'à ce que le numérateur et le dénominateur
aient 1 et
seulement 1 comme diviseur commun.
Le
résultat de la simplification d'une fraction est souvent appelé fraction
irréductible.
Ainsi une fraction est dite irréductible si et
seulement si elle n'est plus simplifiable, c'est-à-dire son numérateur et
son dénominateur sont deux nombres ayant 1et
seulement 1 comme diviseur commun.
Simplifier une fraction ou la rendre irréductible veut dire la même chose.
Exemples de simplification de fractions :
![]()
35 = 5 × 7 et 125 = 5 × 5 × 5 ; donc 5 est un diviseur commun de 35 et 125.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
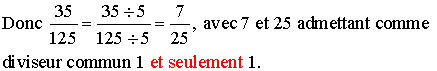
![]()
28 = 4 × 7 et 91 = 7 × 13 ; donc 7 est un diviseur commun de 28 et 91.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
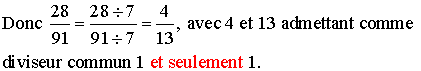
![]()
144
= 12 ×
12 = 3 ×
4 ×
3 ×
4 = 3 × 3 × 4 × 4 et
4320 = 432 × 10 = 3 × 144 × 2 × 5 = 3 × (3 × 3 × 4 × 4) × 2 × 5 =
2 × 3 × 3 × 3 × 4 × 4 × 5. Donc 3 ×
3 × 4 × 4 = 144 est un diviseur commun de
144 et 4320.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
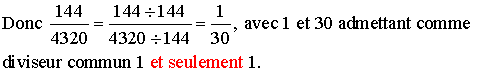
A6- Fraction d'une quantité
Soit Q une quantité quelconque.

Application
:
Un
rectangle a pour longueur 15 cm et pour largeur 9 cm.
On réduit sa longueur d'un cinquième et sa largeur de tiers.
Calculer sa nouvelle surface et déduis de combien elle a été réduite.
A7- Écritures
fractionnaires d'un entier naturel et d'un nombre décimal
Tout
nombre entier naturel peut s'écrire sou la forme d'une fraction ayant 1 comme
dénominateur.
Exemples :
![]()
Tout nombre décimal peut s'écrire sous forme d'une fraction dont le dénominateur est une puissance de 10.
Exemples :
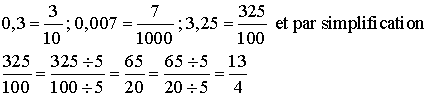
Quatrième et troisième
A- Opérations sur les fractions
A1- Addition
La somme de fractions de même dénominateur est égale à une fraction dont le numérateur est la somme de numérateurs et le dénominateur est le dénominateur commun.
Exemples :
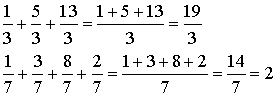
Somme de deux fractions de dénominateurs différents.
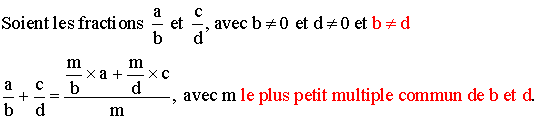
Généralisation de l'addition
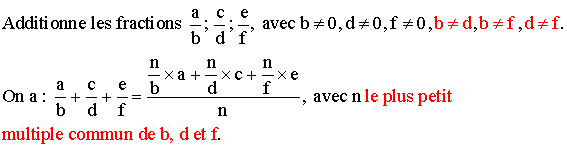
Exemple :
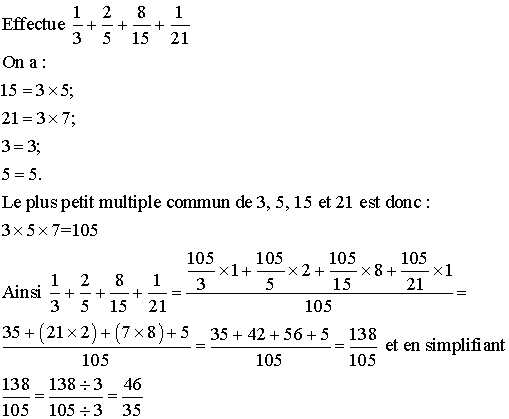
A2- Soustraction
Remarque importante : dans l'ensembles des fractions positives, la soustraction n'est possible que si le premier terme est supérieur ou égal au second terme.
Ainsi :
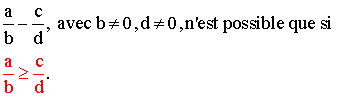
Quant à la méthode, elle est identique à celle évoquée pour l'addition.
Exemples
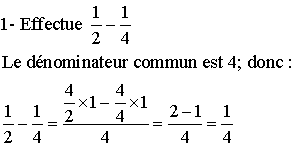
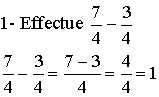
A3- Multiplication ou produit
La multiplication ou le produit de fractions est une fraction dont le numérateur est le produit des numérateurs et le dénominateur est le produit des dénominateurs.
Exemples
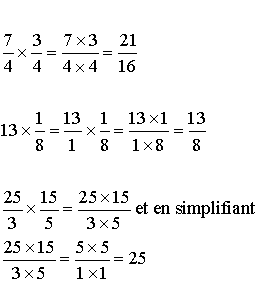
A4- Division

Exemples
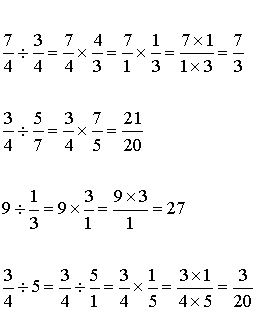
Troisième
A- Diviseurs et multiples communs à plusieurs nombres entiers
A1- Diviseurs communs
A11- Définitions
Soit
a un nombre entier quelconque.
On rappelle qu'un nombre b différent de 0 divise a si
et seulement s'il existe un nombre k tel que :
a = k × b
Dans ce cas on dira que b est un diviseur de
a ou a est divisible par b ou encore a est un multiple
de b.
Exemples :
3 divise 12 car 12 = 4 × 3;
7 divise 21 car 21 = 3 × 7;
13 divise 13 car 13 = 1 × 13;
3 divise 0 car 0 = 0 × 3;
1 divise 27 car 27 = 27 × 1;
1 divise 12 car 12 = 12 × 1;
A12- Propriétés
Tout nombre entier naturel différent de 0 divise 0; donc 0 admet une infinité de diviseurs tous différents de 0.
1 est diviseur de tout nombre entier naturel.
Tout nombre entier naturel différent de 0 admet au moins deux diviseurs : lui - même et 1.
A13- Recherche des diviseurs d'un nombre entier naturel
Considérons le nombre 12.
Ses diviseurs sont 1; 2; 3; 4; 6 et 12.
Ce sont là tous les diviseurs de 12.
L'ensemble des diviseurs de 12 est noté :
![]()
Si un nombre entier naturel a, différent de 0, n'admet que
lui-même et 1 comme diviseurs, c'est-à-dire :
![]()
alors a sera appelé nombre premier.
Exemple :
1; 2; 3; 5; 7; 11; 13; 17 sont tous des nombres premiers.
Comment donc a-t-on procédé pour trouver tous les diviseurs de 12 ?
Il faut d'abord trouver le plus petit nombre
premier différent de 1 et diviseur de 12; c'est donc 2.
On divise 12 par 2 et on obtient 6 comme quotient.
A son tour 6 admet également pour diviseur le plus petit nombre premier
différent de 1qui est 2.
On divise donc 6 par 2 et on obtient 3 comme quotient.
3 est premier; donc ses seuls diviseurs sont 1 et 3.
Finalement on a : 12 = 2 × 2 × 3 × 1 = 22 × 3 × 1
On a donc écrit 12 sous la forme d'un produit de puissances de nombres premiers.
C'est cette écriture qui nous a permis de
trouver tous les diviseurs de 12 : ce sont tous les
diviseurs de 22 × 3 × 1, c'est-à-dire 1;
2; 3;
22 × 1 = 4; 2
× 3 = 6; 22 × 3 = 12.
Prenons un autre exemple : cherchons tous les diviseurs de 144.
Le plus petit nombre premier différent de 1 et
divisant 144 est 2. Donc divisons 144 par 2; on
obtient 72 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 72 est 2.
Donc divisons 72 par 2; on obtient 36 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 36 est 2.
Donc divisons 36 par 2; on obtient 18 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 18 est 2.
Donc divisons 18 par 2; on obtient 9 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 9 est 3.
Donc divisons 9 par 3; on obtient 3 comme quotient.
3 est premier; donc ses seuls diviseurs sont 1 et 3.
Finalement 144 = 24 × 32 ×
1 et les diviseurs de 144 sont :
1; 2; 3;
22 = 4; 2
× 3 = 6; 23 = 8; 32
= 9; 22
× 3 = 12; 24 =16;
2 × 32
= 18;
23 × 3 = 24; 22
× 32 = 36; 23
× 32 = 72; 24
× 32 × 1 = 144 et ainsi :
![]()
A14- Recherche des diviseurs communs de deux nombres entiers naturels différents de 0
Soient deux nombres entiers naturels a et b distincts et différents de 0.
un diviseur commun de a et b est un nombre différent
de 0 divisant à la fois a et b.
L'ensemble des diviseurs communs de a et b est donc :
![]()
Si
cet ensemble est égal à {1} alors on dira que a et b sont premiers
entre eux.
Ainsi 12 et 25 ont pour diviseur commun 1et seulement 1;
donc 12 et 25 sont premiers entre eux.
Exemple :
L'ensemble des diviseurs communs de 12 et 144 est :
![]()
Ainsi le plus grand diviseur commun (abréviation : p.g.d.c) de 144 et 12 est unique et est égal à 12.
A15- Simplification d'une fraction

A16- Applications
1ère Application : simplifions les fractions suivantes :
![]()

Écriture
de 680 :
Le plus petit des nombres premiers différent de 1et divisant 680 est 2;
donc divisons 680 par 2; on obtient pour quotient 340.
Le plus petit des nombres premiers différent de 1et divisant 340 est 2;
donc divisons 340 par 2; on obtient pour quotient 170.
Le plus petit des nombres premiers différent de 1et divisant 170 est 2;
donc divisons 170 par 2; on obtient pour quotient 85.
Le plus petit des nombres premiers différent de 1et divisant 85 est 5;
donc divisons 85 par 5; on obtient pour quotient 17.
17 est premier.
On a donc :
680 = 2 × 2 × 2 × 5 × 17 = 23 × 5 × 17
Écriture de 1240 :
Le plus petit des nombres premiers différent de 1et divisant 1240 est 2; donc divisons 1240 par 2; on obtient pour quotient 620.
Le
plus petit des nombres premiers différent de 1et divisant 620 est 2;
donc divisons 620 par 2; on obtient pour quotient 310.
Le
plus petit des nombres premiers différent de 1et divisant 310 est 2;
donc divisons 310 par 2; on obtient pour quotient 155.
Le
plus petit des nombres premiers différent de 1et divisant 155 est 5;
donc divisons 155 par 5; on obtient pour quotient 31.
31 est premier.
On a donc :
1240 = 2 × 2 × 2 × 5 × 31 = 23 × 5 × 31
Tout ce qui vient d'être dit se résume par les dispositions suivantes :
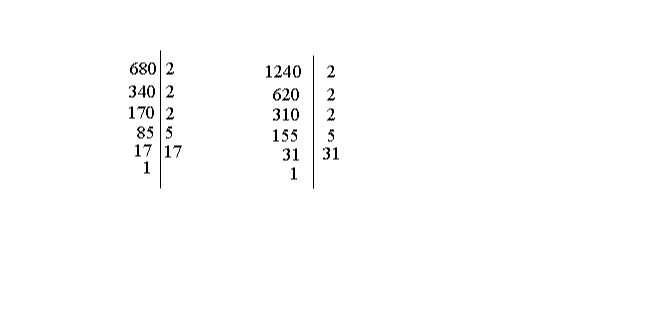
Le
p.g.c.d de 680 et 1240 s'obtient en prenant les facteurs premiers communs
et de plus faibles puissances et en effectuant leur
produit.
Ce sont 23 et 5. Leur produit est 23 × 5; donc le p.g.c.d
de 680 et 1240 est 23 × 5 = 8 × 5 = 40.
Pour
simplifier la fraction donnée, il suffit donc de diviser le numérateur et le
dénominateur par 40 et on obtient la fraction irréductible :
![]()
A toi de simplifier les trois autres fractions.
A2- Multiples communs
A21- Propriété
0 est multiple de tout nombre entier naturel différent de 0.
A22- Recherche des multiples d'un nombre entier naturel différent de 0
Soit a un nombre entier différent de 0.
L'ensemble des multiples de a est un ensemble infini et est défini par compréhension da la manière suivante :
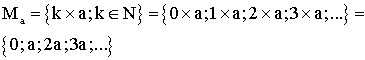
Exemple :
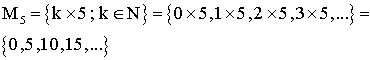
A23- Recherche des multiples communs de plusieurs nombres entiers naturels différents de 0
Soient plusieurs nombres entiers naturels a, b, c, d tous différents de 0.
L'ensembles des multiples communs de a, b, c et d est :
![]()
Exemple :
![]()
A24- Recherche du plus petit multiple commun de plusieurs nombres entiers naturels différents de 0
Soient plusieurs nombres entiers naturels a, b, c, d tous différents de 0.
L'ensembles des multiples communs de a, b, c et d est :
![]()
Cet ensemble possède un élément x0 tel que :
![]()
C'est le plus petit élément appartenant à l'intersection précitée. On le nomme plus petit multiple commun (abréviation : p.p.m.c) de a, b, c et d.
Pour trouver cet élément, on écrit d'abord les nombres a, b, c et d sous la forme de produits de puissances de facteurs premiers, puis on prend le produit de plus grandes puissances de ces facteurs, que ces derniers soient ou non communs.
Exemples :
Trouvons le p.p.m.c de 1240 et 680.
On a :

Donc
680 = 2 × 2 × 2 × 5 × 17 = 23 × 5 × 17
1240 = 2 × 2 × 2 × 5 × 31 = 23 × 5 × 31
p.p.m.c (680;1240) = 23 × 5 × 17 × 31 = 40 × 17 × 31 = 21080
Trouvons le p.p.m.c
de 1360 et 31000.
On doit d'abord trouver :
1360 = 24 × 5 × 17
31000 = 23 × 53 × 31
p.p.m.c
(1360;31000) = 24 × 53 × 17 × 31 = 16 × 125 × 17 ×
31 =
1054000
A25- Application de la notion de p.p.m.c
Dans une addition ou une soustraction de fractions, le dénominateur commun est le p.p.m.c des différents dénominateurs de ces fractions.
Exemple :

A26- Applications
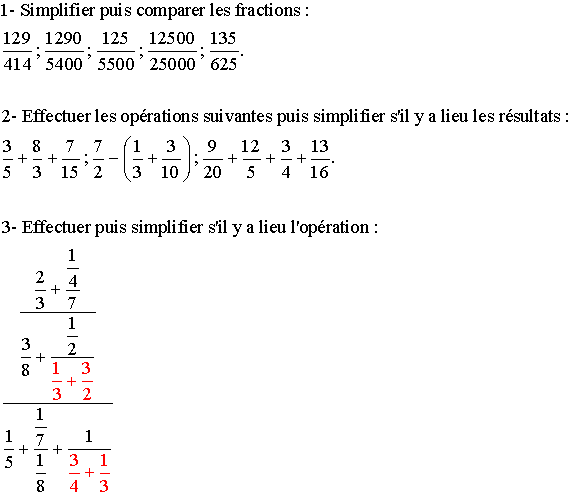
Indications
pour cet exercice :
Tu commences par les opérations élémentaires indiquées en rouge, puis
tu les remplaces par les résultats trouvés. Tu poursuis ensuite en procédant
de la même manière, jusqu'au dernier résultat et enfin tu simplifie s'il y a
lieu.
angles
(groupe ciblé : troisième)
Angles d’un triangle
On a appris dans les classes
antérieures qu’un triangle se compose de trois sommets
et de trois côtés qui, pris deux à deux, forment
un angle dont le sommet est l’un des
sommets du triangle.
Par conséquent, un triangle possède trois angles de ce type appelés angles intérieurs.
Propriété :
La somme des mesures des angles
intérieurs d’un triangle est égale à 180°.
Dans un triangle,
tout angle adjacent et
supplémentaire à un angle intérieur est
appelé
angle extérieur.
Soit un triangle (ABC)
quelconque pour lequel on a prolongé ses trois côtés [AB],
[BC] et [AC] de manière que (AB) soit égale à (x’x), (BC) soit égale (y’y) et
(AC)
soit égale à (z’z).
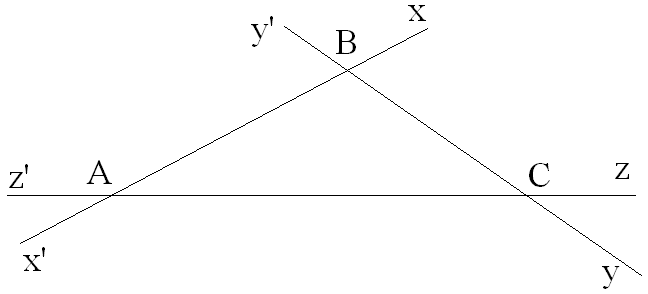
Ses angles intérieurs sont :

La somme de leurs mesures est :

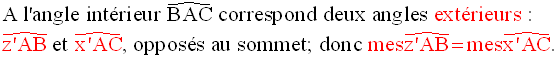
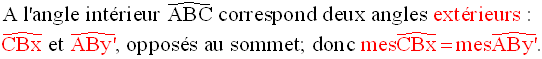
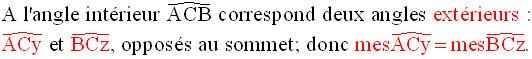
Propriété :
Dans un triangle,
la mesure d’un quelconque de ses angles extérieurs est égale à la
somme des mesures des deux angles intérieurs qui ne lui sont pas adjacents.
Démonstration
La démonstration est établie
pour un des angles extérieurs en A.
Elle est la même pour les autres.

Or, on sait que :
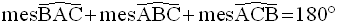
Donc,
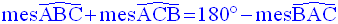
Deux quantités égales à une même troisième sont égales et finalement on obtient :

Position relative d’un angle par rapport à un cercle
On donne un cercle quelconque de centre O et de rayon r, noté C(O , r).
On appelle angle au centre tout angle dont le sommet est confondu avec le centre O.

Tout angle au centre intercepte un arc du cercle.

Etant donné un arc
quelconque du cercle, on appelle
mesure de cet arc, la
mesure de
l’angle au centre qui l’intercepte.

Il ne faut pas confondre la longueur d’un arc et sa mesure ; ce sont deux notions différentes.
Par exemple, on dira que la longueur d’un arc est de 5cm, alors que sa mesure est de 30°.
Ainsi, à l’angle au centre
mesurant 360° correspond le cercle tout entier dont la longueur
est son périmètre.
On a donc la correspondance :

C’est cette correspondance
qu’on utilise pour calculer la longueur (resp. la mesure)
d’un arc donné sur un cercle, connaissant la mesure (resp. la longueur) de cet
arc.
Exemple :

D’où la propriété qui en découle :
Sur un même cercle, deux arcs au centre de même mesure ont même longueur et réciproquement.
Cette propriété
n’est plus vraie pour deux arcs, l’un appartenant
à un cercle et
l’autre à un cercle qui est concentrique au
premier, interceptés par un même angle
au centre.
En effet ces deux arcs ont même mesure, cependant leurs longueurs sont différentes puisqu’elles sont fonctions des rayons différents de ces deux cercles concentriques.
A titre d’exercice, je te demande de construire une figure illustrant cette remarque.
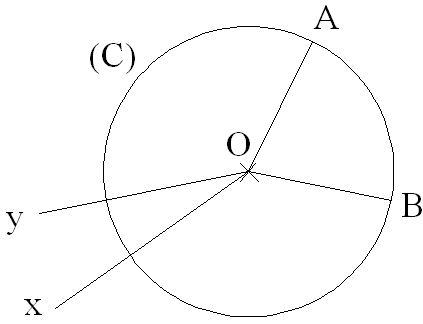
On donne un cercle quelconque de centre O et de rayon r, noté C(O , r).
On appelle angle inscrit tout angle dont le sommet appartient à ce cercle.

Propriété :
La mesure de tout angle inscrit est égale à la moitié de la mesure de
l’arc qu’il intercepte.
Démonstration
1er cas :
le support d’un des côtés de l’angle inscrit est confondu avec celui d’un
diamètre
du cercle
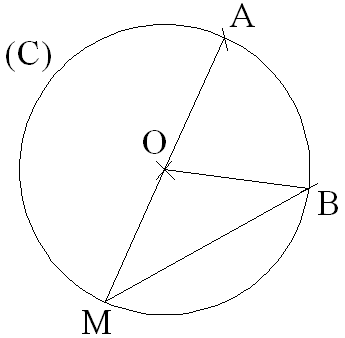
On joint O à B.
OM et OB sont égales au rayon du cercle ; donc le triangle (MOB) est isocèle.

2ème cas :
le centre O du cercle est à l’intérieur de l’angle inscrit
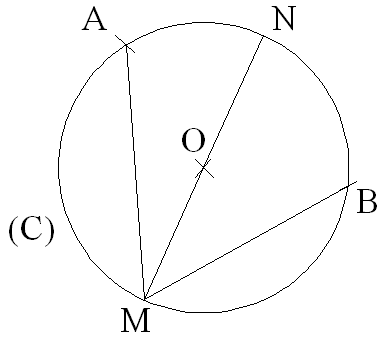
On joint M à O.
La droite (MO) rencontre le cercle en un deuxième point N.
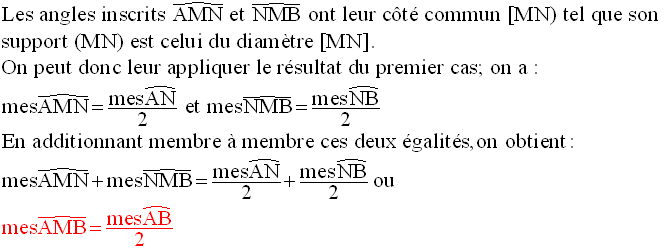
3ème cas :
le centre O du cercle est à l’extérieur de l’angle inscrit
A titre
d’exercice, je te laisse démontrer la propriété pour ce troisième cas.
La démonstration est la même que celle du deuxième cas, à la seule différence
qu’il faudra
retrancher des quantités au lieu de les
additionner.
Cas particulier : un des côtés de l’angle inscrit est tangent au cercle
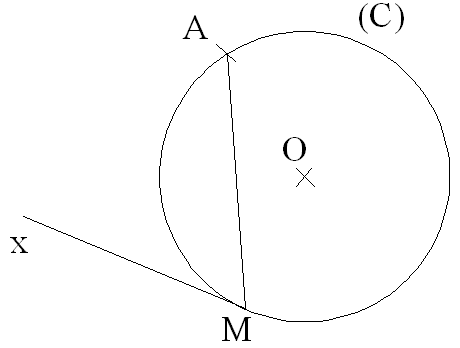

On appelle angle intérieur tout angle dont le sommet est à l’intérieur du cercle.
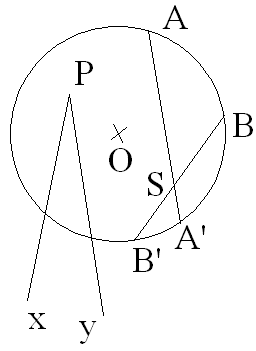
Propriété :
La mesure de tout angle intérieur est égale à la moitié de la somme
des mesures des
deux arcs, l’un intercepté par cet angle et l’autre intercepté par
l’angle intérieur qui
lui est opposé au sommet.
Démonstration
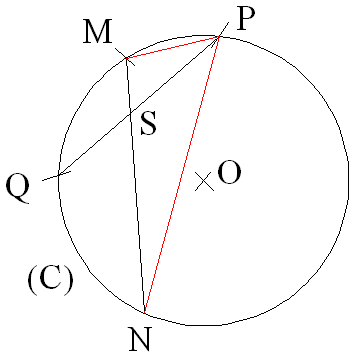
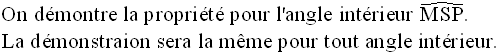
On joint M à P et N à P.

Tout
angle dont le sommet est à l’extérieur du cercle
et dont chacun des côtés est
sécant ou tangent au cercle est appelé angle
extérieur.
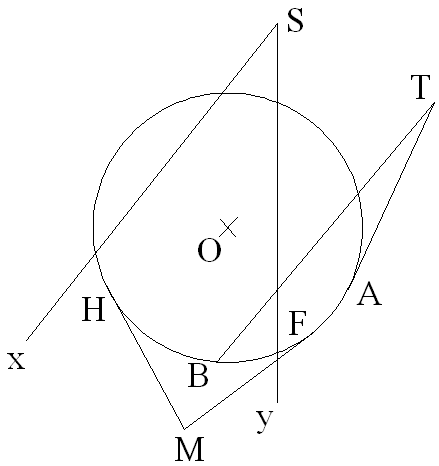

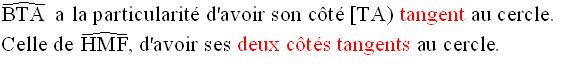
Propriété :
La mesure de tout angle extérieur est égale à la moitié de la
différence des mesures des deux arcs interceptés par ses côtés.
Démonstration
1er cas : les deux côtés de l’angle extérieur sont sécants au cercle

On joint A’ à B.
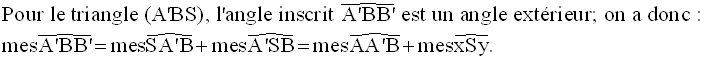
Par conséquent,
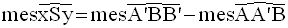
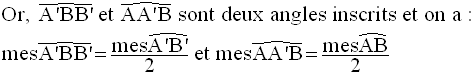
Finalement , on obtient :

2ème cas : l’un des côtés est tangent au cercle et l’autre, lui est sécant
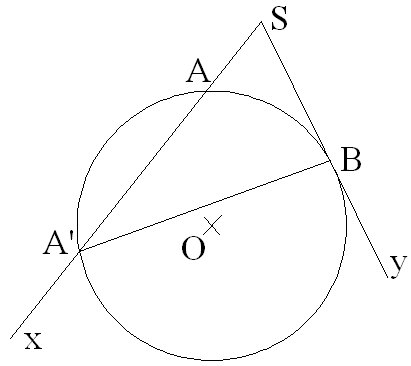
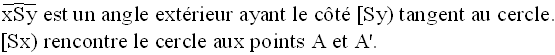
On joint A’ à B.
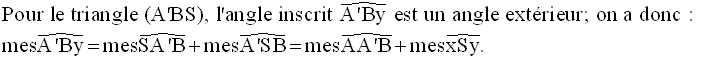
Par conséquent,
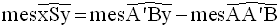
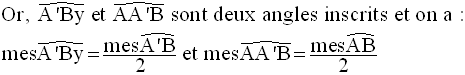
Finalement , on obtient :

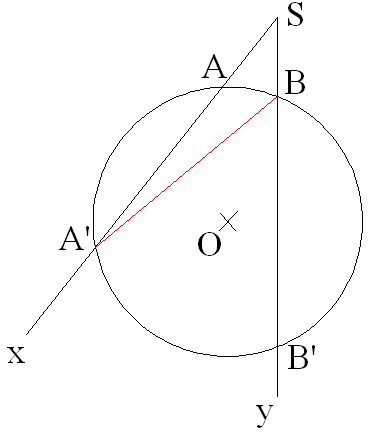
3ème cas : les deux côtés sont tangents au cercle
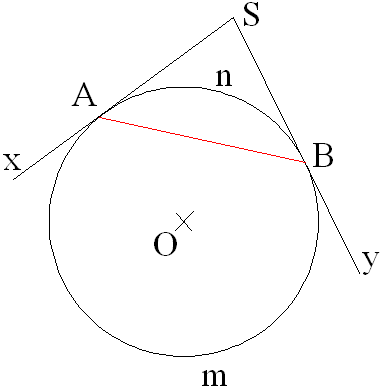
On joint A à B.
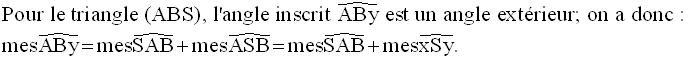
Par conséquent,

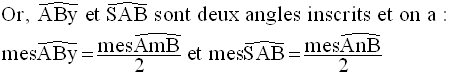
Finalement , on obtient :

Exercices
1)
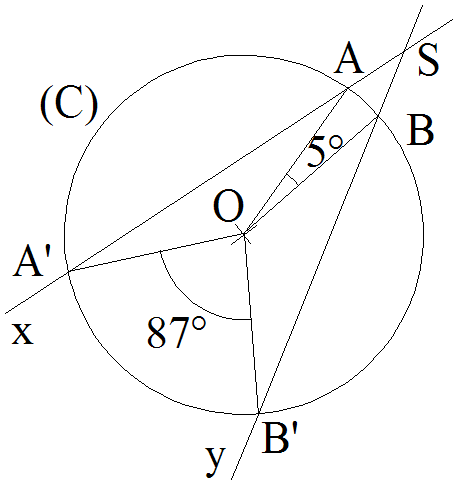
On donne la figure suivante :
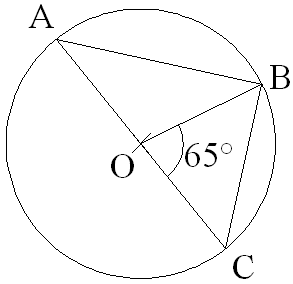
Calcule les mesures des angles suivants :

Solution
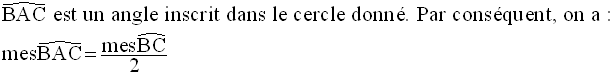
On obtient finalement :
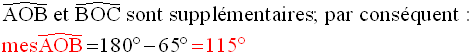

On obtient finalement :
2)
On donne la figure suivante :
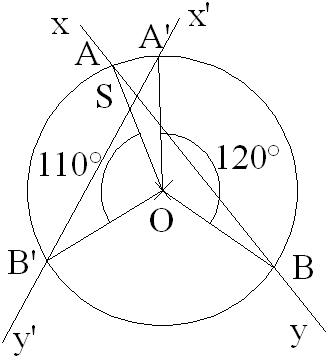
(xy) rencontre le cercle aux points A et B ; (x’y’) le rencontre aux points A’ et B’.
(xy) et (x’y’) se coupent au point S.
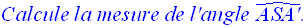
Solution

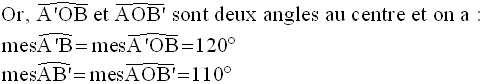
Par conséquent, on obtient :
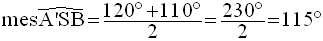
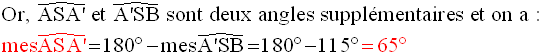
3)
On donne dans un plan deux points distincts et fixes A et B.
Trouve l’ensemble des points M tels que :

Solution
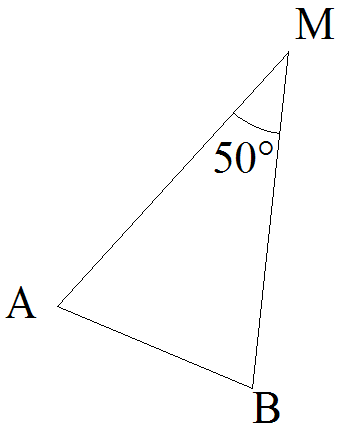
Soit la position d’un point M quelconque appartenant à l’ensemble à trouver.
Soit (C) le cercle circonscrit au triangle (AMB).
Soit O le centre de ce cercle.
O appartient à la médiatrice d du segment [AB].
Or, A et B étant fixes, d l’est également.
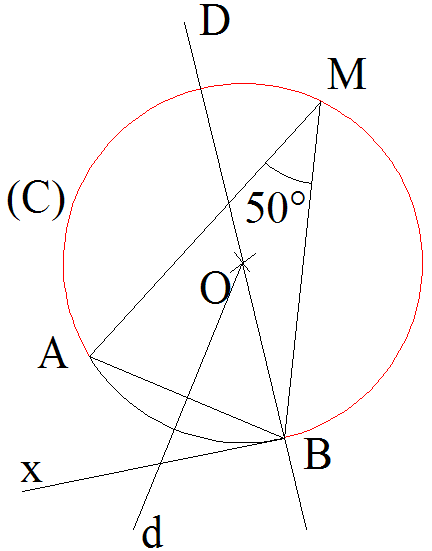
Menons de B la demi-droite [Bx), tangente à (C) au point de tangence B.
[Bx) étant une tangente à
(C) au point B et [OB] étant un rayon de ce cercle dont
l’extrémité est B, [Bx) est donc perpendiculaire à (OB).
O appartient donc à la droite D perpendiculaire à [Bx) au point B.

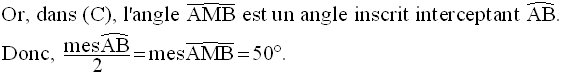
Par conséquent, on a :

A et B étant fixes et la
mesure d’angle de 50° étant une constante, la
demi-droite [Bx)
est donc fixe.
D étant perpendiculaire à cette demi-droite fixe au point B est également fixe.
O appartenant simultanément à deux droites fixes d et D est fixe.
Par conséquent,
le cercle (C) circonscrit au triangle (AMB), ayant son
centre O
fixe et son rayon OA ou OB constant (puisque O et A sont fixes), est fixe.
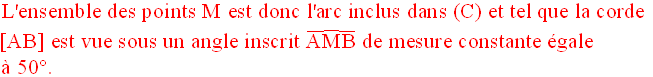
Par définition, cet arc (en rouge sur la figure) est appelé arc capable.
Remarque :
L’énoncé de cet exercice aurait pu être le suivant :
On donne dans un plan deux points distincts et fixes A et B.
Un point M de ce plan se déplace tel que :

Trouve le lieu géométrique de M.
La solution reste la même.
4)
On donne la figure suivante :
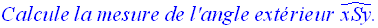
Solution

Par ailleurs, on a :
Finalement, on obtient :

5)
On donne un cercle C(O , r).
Par un point S
situé à l’extérieur de ce cercle, on mène les deux tangentes (Sx)
et (Sy) à ce même cercle.
Le point de tangence relatif à (Sx) est A et celui relatif à (Sy) est B.

Démontre que le triangle (SAB) est équilatéral.
Solution

Par ailleurs, on sait que sur les deux tangentes à un cercle issues d’un même point, les segments délimités par ce point et les deux points de tangence ont même longueur.
Par conséquent, on a :
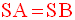
Le triangle (SAB) ayant un angle de mesure 60° et deux côtés de même longueur, est équilatéral.
6)
On donne deux cercles sécants C(O, r) et C’(O’ , r).
Chacun de ces cercles passe par le centre de l’autre.
Les intersections de C(O, r) et C’(O’ , r) sont les points A et B.
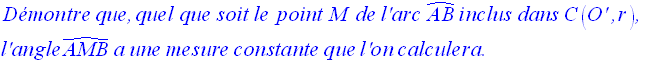
Solution
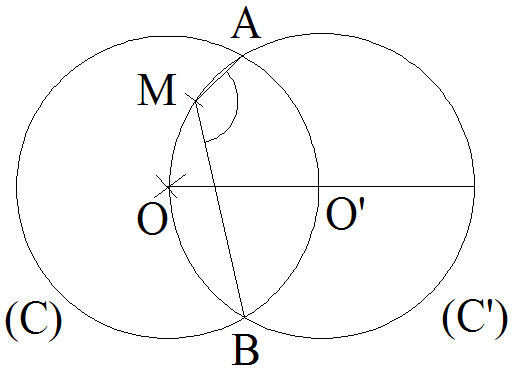
O’ appartenant à (C), on a :
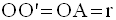
O appartenant à (C’), on a :
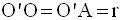
Ainsi,
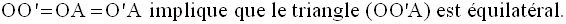
La symétrie axiale d’axe
(OO’) permet d’en déduire que le triangle (OO’B) est
également équilatéral.
Par conséquent, on a :
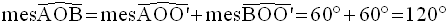
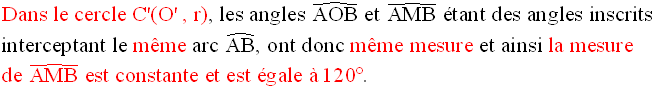
7)
a-
Dans un plan, on donne un quadrilatère (ABCD) inscrit dans un cercle C(O , r).
Démontre que les angles intérieurs de ce quadrilatère sont deux à deux opposés et supplémentaires.
b-
On donne dans un plan un quadrilatère convexe (ABCD) tel que deux de ses angles intérieurs et opposés sont supplémentaires.
Démontre que (ABCD)
est inscrit dans un cercle, autrement dit, que ses quatre sommets
sont situés sur un même cercle.
On dira alors que les points A, B, C et D sont cocycliques.
c-
Déduis des conclusions des questions a et b une condition nécessaire et suffisante pour qu’un quadrilatère convexe soit inscriptible dans un cercle.
Je te laisse résoudre cet exercice.
a-
Pour cette question, il
suffit d’effectuer la somme des mesures de deux angles intérieurs
et opposés de ce quadrilatère, sachant que ces angles
sont des angles
inscrits.
b-
Pour cette question, on
considère le cercle passant par trois quelconques des quatre
sommets du quadrilatère, par exemple A, B et C et on démontre que le quatrième
sommet, D, appartient à ce cercle.
Pour cela, il suffit de
raisonner par l’absurde : ce quatrième sommet D peut prendre
trois positions par rapport au cercle passant par les trois
autres sommets.
S’il est à l’intérieur ou à l’extérieur
du cercle, l’angle intérieur du quadrilatère, en D,
a alors pour mesure la demi - somme ou la demi - différence des mesures de deux
arcs
et ceci aboutit à une contradiction avec l’hypothèse de
supplémentarité
de deux angles
opposés, en D et en B, du quadrilatère.
c-
Pour qu’un quadrilatère
convexe soit inscriptible dans un cercle, il faut et il
suffit que
deux angles intérieurs opposés de ce
quadrilatère soient supplémentaires.
pyramide et cône
(groupe ciblé : troisième)
Convention
Dans tout ce qui suit, tout élément caché (non directement vu) d’un
solide représenté dans l’espace à trois dimensions sera représenté par une ligne
discontinue
1- Les pyramides
1-1 Définitions et propriétés
Dans un plan de l’espace, on
considère un polygone quelconque (P).
On donne un point S de cet espace n’appartenant pas au
plan de (P).
On joint S à chacun des sommets de (P).
Le solide de cet espace, délimité par S et (P), est appelé pyramide.
S sera appelé sommet de cette pyramide et (P) sera appelé sa base.
Un segment qui joint S à un
sommet quelconque de (P) sera appelé arête latérale
de la pyramide.
Tout triangle formé par deux
arêtes latérales adjacentes et le côté de (P)
intercepté
par ces deux arêtes latérales sera appelé face
latérale de la pyramide.
La droite
orthogonale au plan de (P), abaissée du sommet S,
rencontre ce plan
au point H ; le segment [SH] sera appelé
hauteur de la pyramide.
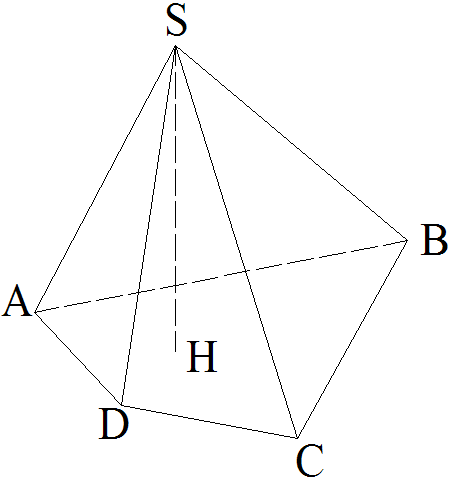
Figure 1 : pyramide [S,(ABCD)]
Dans cette figure, le solide
noté [S,(ABCD)] est une pyramide dont la base est
le quadrilatère (ABCD).
Son sommet est S.
Les segments [SA], [SB], [SC] et [SD] sont ses arêtes latérales.
Les triangles (SAB), (SBC), (SCD), (SDA) sont ces faces latérales.
La droite orthogonale au
plan contenant (ABCD) abaissée du sommet S rencontre
ce plan au point H ; [SH] est la hauteur de cette pyramide.
Propriété
Dans une pyramide, toutes les faces latérales sont des triangles.
On dira que [S,(P)] est une
pyramide régulière si et seulement si sa
base (P)
est un polygone régulier et le support de sa hauteur passe par le
centre de ce
polygone régulier.
Propriété
Dans une pyramide régulière, toutes les arêtes latérales ont même longueur.
Deux cas particuliers
1er cas : base triangulaire
Lorsque la
base d’une pyramide est un
triangle, cette pyramide sera appelée
tétraèdre.
(Figure 2)
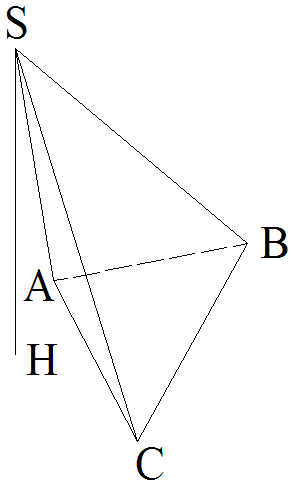
Figure 2 : [S,(ABC)] est un tétraèdre
2ème cas :
tétraèdre dont la base et les trois faces latérales sont toutes des triangles
équilatéraux de même longueur de côtés
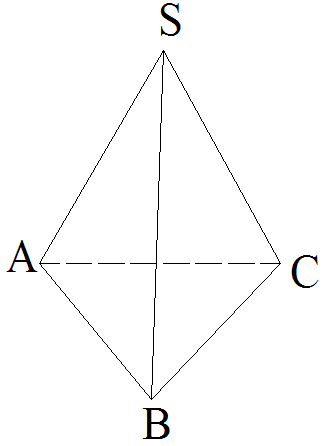
Figure 3 : [S,(ABC)] est un tétraèdre régulier
Lorsque la base et les trois
faces latérales d’un tétraèdre sont toutes des triangles
équilatéraux de même longueur de côtés,
alors ce tétraèdre est régulier et sera appelé
tétraèdre régulier.
(Figure 3)
1-2 Aire latérale d’une pyramide
L’aire latérale d’une pyramide est la somme des aires de ses faces latérales.
Cas particulier du tétraèdre régulier
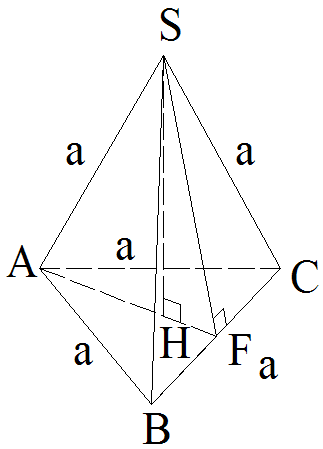
On donne un tétraèdre
régulier [S,(ABC)] dont la longueur commune des arêtes
latérales est a.
On a également :
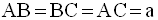
[SH] étant sa hauteur, la
droite (SH) passe par le centre H du cercle circonscrit à
la base (ABC) qui est un triangle équilatéral; donc on a :
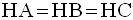
Soit F l’intersection de
(AH) et de [BC] ; [AF] est la médiatrice de [BC] et F est
milieu de [BC].
Dans la face latérale (SBC), [SF] est donc la médiane relative au côté [BC] du triangle équilatéral (SBC).
Or, on sait que dans un
triangle équilatéral, une médiane relative à un des ses côtés est simultanément
médiatrice de ce côté ; par conséquent, dans (SBC), [SF] est médiatrice
de [BC] et le triangle (SFC) est un triangle demi-équilatéral, rectangle en F.
Le théorème de Pythagore appliqué à ce triangle donne :
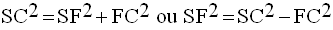
Or,
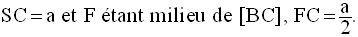
Donc,
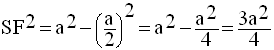
Par conséquent, on obtient :
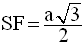
En posant A l’aire de la face latérale (SBC), on obtient :
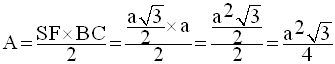
Comme dans un tétraèdre
régulier, les trois faces latérales sont des triangles
équilatéraux de même longueur de côtés,
l’aire latérale de ce tétraèdre est donc :
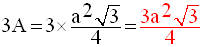
1-3 Volume d’une pyramide
Soit dans l’espace une pyramide quelconque [S,(P)] de sommet S et de base polygonale (P).
Si B
est l’aire de la base (P) et si
h est la longueur de
la hauteur de cette pyramide,
alors le volume V
de cette dernière est égal à :
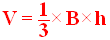
Cas particulier du tétraèdre régulier

On sait que le pied H de la
hauteur de cette pyramide est le centre du cercle
circonscrit à la base qui est un triangle équilatéral (ABC).
H est également centre du
cercle inscrit à ce triangle équilatéral ; donc [CH) est
bissectrice de l’angle au sommet C.
De plus, (AF) ou (HF) étant
médiatrice de [BC] ; (HF) est perpendiculaire à (BC)
ou (FC).
Par conséquent, dans le triangle (CHF), rectangle en F, on a :
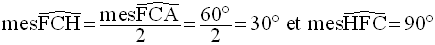
Le triangle (CHF) est donc un triangle demi-équilatéral.
On sait que dans un triangle
demi-équilatéral dont l’hypoténuse a pour longueur L,
la longueur du côté opposé à l’angle de mesure 60° est égale à :
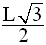
Par conséquent, dans (CHF), on obtient :
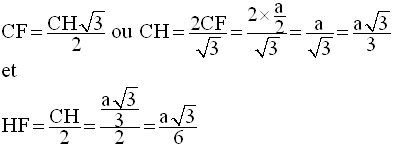
Le théorème de Pythagore appliqué au triangle rectangle (SHF) donne :
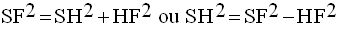
On a démontré plus haut que :
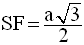
Par conséquent, on obtient :
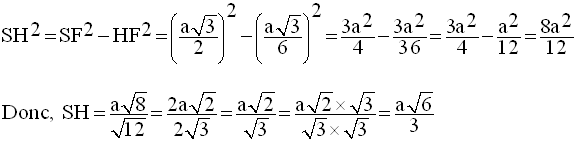
On sait que la base et toutes les faces latérales d’un tétraèdre régulier sont des triangles équilatéraux de même longueur de côtés.
Donc, ils ont tous même aire et celle–ci a été calculée plus haut et est égale à :
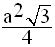
Donc la base de ce tétraèdre a pour aire :
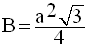
Le volume est donc :
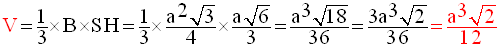
2- Les cônes
2-1 Définitions et propriétés
On donne dans un plan un cercle C(O,r) de centre O et de rayon r.
D’un point S n’appartenant
pas au plan de ce cercle, on mène une droite d
rencontrant C(O,r) au point G.
Lorsque G parcourt
complètement le cercle C(O,r), la demi-droite [SG) génère dans
l’espace une surface (s).
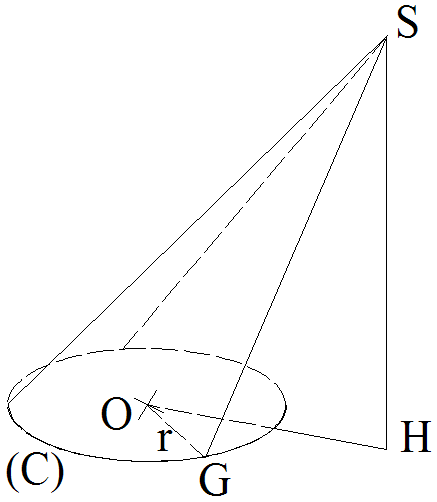
Le solide délimité par (s) et C(O,r) est appelé cône et est noté :
[S , C(O,r)].
S est appelé sommet de ce cône.
Le cercle C(O,r) est appelé directrice de ce cône et le segment [SG] est sa génératrice.
L’aire de la surface (s) est appelée aire latérale de ce cône.
La droite (SH) passant par S
et orthogonale au plan de C(O,r) coupe ce plan au
point H.
Le segment [SH] est appelé
hauteur du cône.
Un cas particulier
Lorsque
la hauteur d’un cône passe par le centre de sa base
circulaire, ce cône sera
alors appelé cône de révolution.
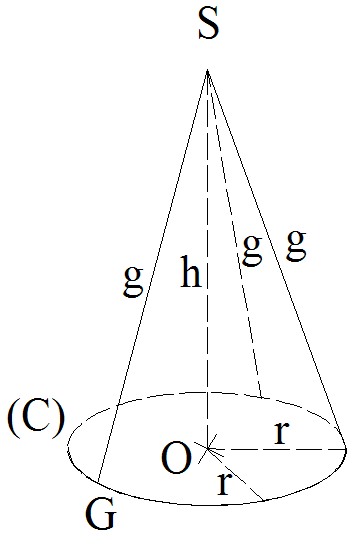
2-2 Aire latérale d’un cône de révolution
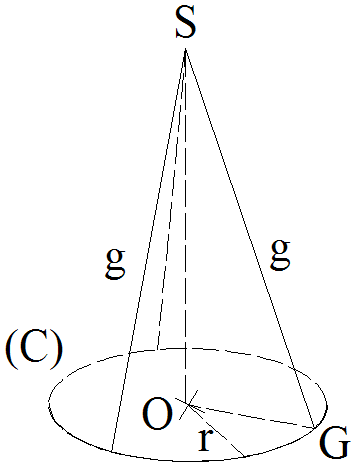
Soit un cône de révolution quelconque [S , C(O,r)].
Si on découpe sa surface
latérale selon une génératrice [SG] et on développe
cette surface, on obtient le schéma suivant :
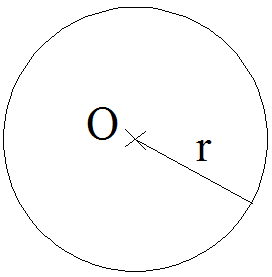
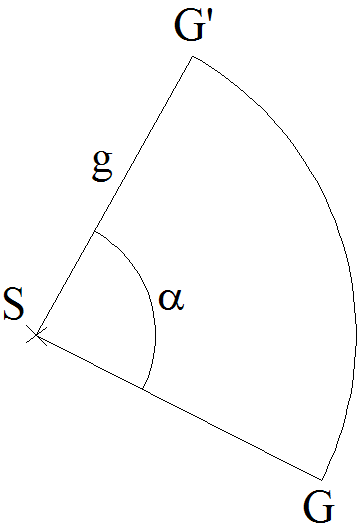
Ce schéma représente la base
circulaire de ce cône, de centre O et de rayon r, ainsi
que le développement de sa surface latérale.
On obtient ainsi le patron de ce cône.
Ce patron permet de calculer l’aire latérale de ce cône.
Soit A cette aire.
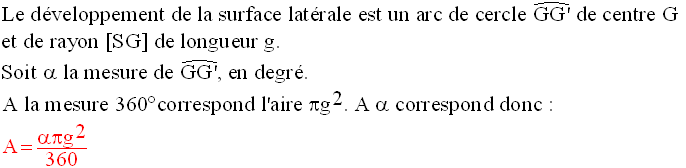
2-3 Volume d’un cône
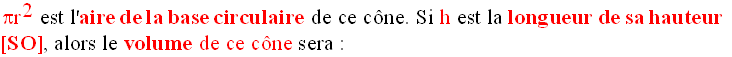
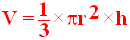
Exercices
1)
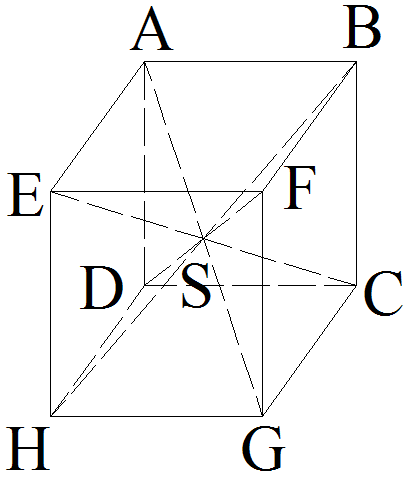
On donne un cube (ABCDEFGH) de centre S.
Trace ses diagonales.
Quelle sont toutes les pyramides régulières de sommet S et de base carrée ?
Solution
Dans un cube, une diagonale
est un segment passant par le centre de ce cube
et
joignant deux sommets opposés.
Ainsi, le cube (ABCDEFGH) possède quatre diagonales qui sont :
[AG], [DF], [BH] et [EC].
On obtient six pyramides régulières de sommet S et de base carrée :
[S , (ABFE)], [S , (DCGH)], [S , (BFGC)], [S , (ADHE)],
[S , (EFGH)] et [S , (ABCD)]
2)
La pyramide [A , (DCGH)] est inscrite dans le cube (ABCDEFGH).
On te demande de calculer le volume de cette pyramide, sachant que la longueur commune des côtés du cube est a.
Solution
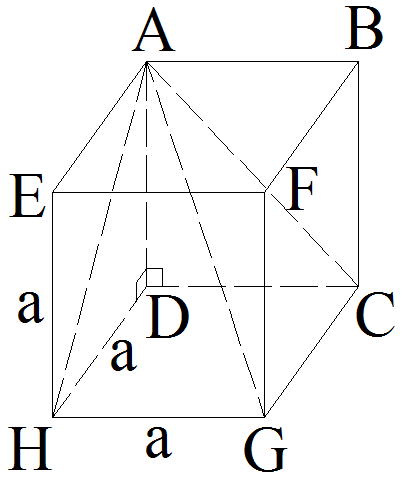
On sait que dans un cube, le support de chaque arête latérale est orthogonale à une base.
Par conséquent, dans la
pyramide [A , (DCGH)], la droite (AD), support de l’arête
latérale [AD], est orthogonale à la base carrée (DCGH) de cette pyramide.
[AD] est donc la hauteur de cette pyramide.
Si V est le volume de cette pyramide, alors :
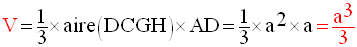
Le volume de cette pyramide est le tiers de celui du cube.
3)
On donne un cylindre dont la base circulaire a pour centre O’ et pour rayon r.
La hauteur [OO’] de ce cylindre a pour longueur OO’ égale à h.
On inscrit
dans ce cylindre une pyramide de sommet O et de base carrée (ABCD)
inscrite dans la base circulaire de ce cylindre.
a-
Démontre que cette pyramide est régulière.
b-
On te demande de calculer, en fonction de h et de r, le volume de cette pyramide.
c-
On retire la pyramide de ce cylindre ; Quel est alors le volume restant ?
Solution
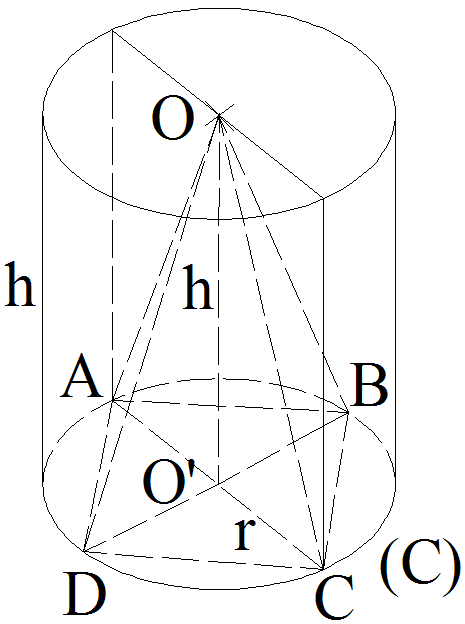
a-
(OO’) est le support de la
hauteur [OO’] commune à ce cylindre et à la pyramide;
de plus elle passe par le centre O’ du carré (ABCD).
Par conséquent, la pyramide [O , (ABCD)] est régulière.
b-
Calcul de l’aire de la base carrée (ABCD) de la pyramide
On sait que dans un carré les diagonales se coupent en leur milieu et à angle droit.
Par conséquent, dans (ABCD),
le triangle (O’BC) est un triangle rectangle en O’
et isocèle.
Le théorème de Pythagore appliqué à ce triangle donne :

L’aire de (ABCD) est donc :
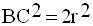
Calcul du volume de la pyramide
Si V est ce volume, alors :
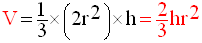
c-
Si V’ est le volume restant, alors :
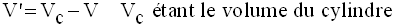
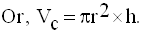
Finalement, on obtient :
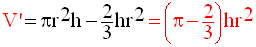
4)
On souhaite
réaliser une pièce d’avion en extrayant, d’un matériau dont la forme
est un cône de révolution, une pyramide, selon le schéma suivant :
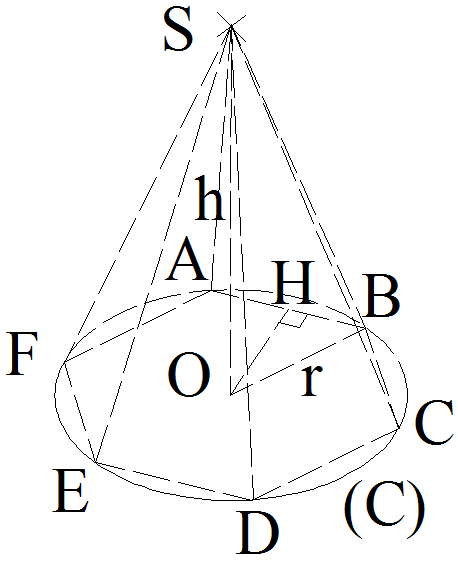
Le cône de
révolution [S , C(O,r)] a pour sommet S et pour base le cercle (C)
de centre O et de rayon r.
La pyramide [S , (ABCDEF)] a pour sommet S et pour base un hexagone régulier (ABCDEF) inscrit dans (C).
La hauteur commune de ce cône et de cette pyramide a pour longueur h.
On demande de calculer le volume de la pièce obtenue.
Solution
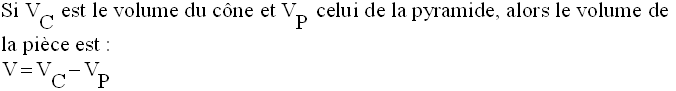
Calcul de VC
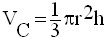
Calcul de VP
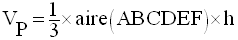
Dans le triangle équilatéral (OAB), on abaisse la hauteur [OH] relative au côté [AB].
Le théorème de Pythagore appliqué au triangle rectangle (OHB) donne :
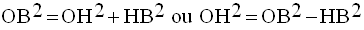
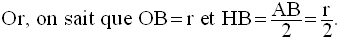
Donc,

On obtient :

L’hexagone régulier (ABCDEF)
étant composé de six triangles équilatéraux tels
que (OAB), a son aire égale à six fois celle de (OAB).
On a donc :
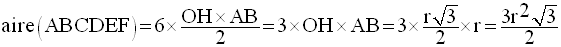
Par conséquent,
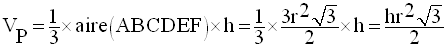
Le volume de la pièce est :
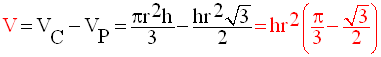
5)
On donne le patron d’un cône de révolution suivant :
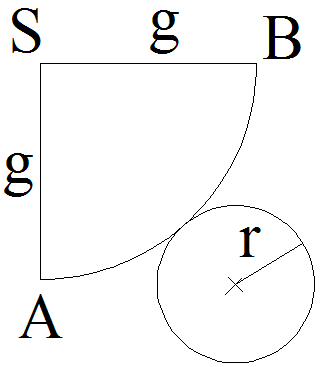
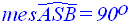
On demande de calculer la longueur g de la génératrice de ce cône de révolution.
Solution
Le périmètre de la base de ce cône est :
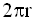
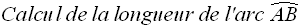
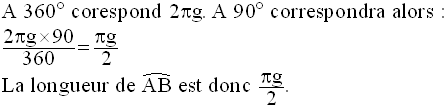
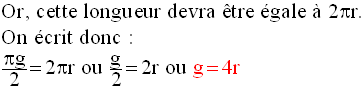
6)
On donne la figure suivante :
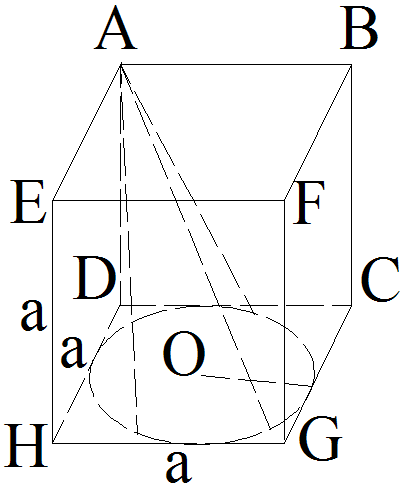
(ABCDEFGH) est un cube dont la longueur commune de ses côtés est a.
Le cercle (C) de centre O est inscrit dans la base carrée (CDHG).
On demande de
calculer le rapport du volume du cône [A , (C)] de sommet A et
de base (C) à celui du cube.
Solution
Soient V le volume du cube et V’ celui du cône.
On a :
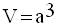
Calcul de V’
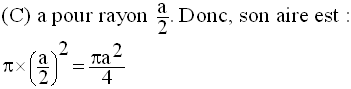
Par conséquent,
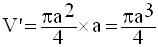
Le rapport de V’ à V est donc :