L'ATELIER DU LYCÉEN
(page 1)
(groupes ciblés : seconde et premières , toutes séries confondues)
les thèmes abordés dans cette page
fonction réelle d'une variable réelle -
généralités
(seconde)
puissances d'un nombre et géométrie
(seconde)
parallélogramme et extremum d'une parabole
(seconde et première S)
système d'inéquations du premier degré et
étude des angles intérieurs d'un triangle
(seconde)
droites et plans parallèles
(première S)
la géométrie analytique dans l'espace
(premières et terminales)
un peu de trigonométrie
(premières S et technologiques)
puissance d'un point par rapport à un cercle
et axes radicaux de deux cercles
(première S)
une transformation trigonométrique
(premières)
fonction réelle d'une variable réelle -
généralités
(groupe ciblé : seconde)
![]()

R peut être représenté par une droite
dite droite réelle , munie d'une origine O
![]()
![]()
Prends un point quelconque M sur cette droite .
![]()
Par définition le
réel k est dit abscisse du point M .
Un intervalle fermé , noté [ab] , est la partie de R telle que :
![]()
Un intervalle ouvert , noté ]ab[ , est la partie de R
telle que :
![]()
Un intervalle semi - fermé à gauche (ou semi - ouvert à droite) , noté [ab[
, est la partie de R telle que :
![]()
Un intervalle semi - fermé à droite (ou semi - ouvert à gauche) , noté ]ab]
, est la partie de R telle que :
![]()
Une fonction réelle d'une variable réelle ,
notée par exemple f , est une
relation dans R qui à tout réel x ,
appelé variable réelle , associe au plus un
réel y appelé image de x par f .
On écrit alors : y = f(x)
.
Notons dans ce cas qu'un élément x de R peut ne pas avoir d'image par f . Mais si l'image de x par f existe alors elle est unique .
On appelle domaine de définition de f la partie de R formée de tous les réels ayant une image par f . Elle sera notée dom (f) .
![]()
0 n'a pas d'image par f dans R ; nous dirons que f n'est pas définie pour x = 0 .
dom (f) = R* .
Soit f une fonction réelle d'une variable
réelle définie sur un intervalle I inclus
dans R , I pouvant être
fermé , semi - fermé ou ouvert .
On dira que f est largement croissante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
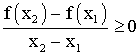
On dira que f est largement décroissante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
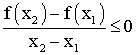
On dira que f est strictement croissante (resp.
strictement décroissante) sur I si , pour tous
x1 , x2 de I tels que x1 différent de x2
on a :
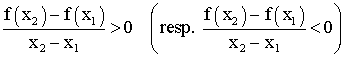
On dira que f est constante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
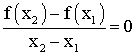
On dira que f est monotone sur I si elle est croissante ou décroissante sur I . Elle sera dite largement monotone sur I si elle est largement croissante ou largement décroissante sur I ; elle sera dite strictement monotone sur I si elle est strictement croissante ou strictement décroissante sur I .
Soit f une fonction numérique définie sur un
ensemble D inclus dans R .
On dira que f admet un maximum en un point x0
appartenant à D ,
si et seulement si , pour tout x appartenant à D ,
![]()
La valeur f(x0
) sera appelée maximum de f sur D .
On dira que f admet un minimum en un point x1 appartenant à D , si
et
seulement si , pour tout x appartenant à D ,
![]()
La valeur f(x1) sera appelée
minimum de f sur D .
f sera dite bornée supérieurement sur D s'il
existe un réel k tel que :
pour tout x appartenant à D ,
![]()
f sera dite bornée inférieurement sur D s'il existe un réel h
tel que :
pour tout x appartenant à D ,
![]()
k et h seront appelés respectivement borne supérieure et borne inférieure
de
f sur D .
R2
étant l'ensemble des couples (x , y) de réels , prenons dans son plan
représentatif deux droites d et d' n'ayant pas le même support et se
coupant en O .
Portons R sur d et sur d' et munissons chacune de ces dernières d'un
vecteur unitaire :
![]()
![]()
![]()
Dans le plan R2 le couple (x'x , y'y) sera appelé repère et
on dira que le plan est ramené
à son repère . L'axe x'x sera dit axe des
abscisses et l'autre , y'y , sera appelé axe des ordonnées .
A tout point du repère correspond un couple (x , y) de R2 et
un seul , et réciproquement .
x sera dit abscisse de ce point et y , son ordonnée .
Le
repère sera dit quelconque si les vecteurs unitaires qui lui sont rattachés
ont des modules (ou normes ou encore longueurs géométriques) différents et
si l'angle formé par
ses deux axes est différent de 90 degrés .
Il sera dit normé si les deux vecteurs unitaires ont le même module (ou norme)
, l'angle formé par ses deux axes étant encore différent de 90 degrés .
Il sera dit orthogonal si l'angle formé par ses deux axes est égal à 90
degrés et les deux vecteurs unitaires de normes différentes.
Il sera dit orthonormé (ou orthonormal) si l'angle formé par ses deux
axes est égal à 90 degrés et si les deux vecteurs unitaires ont de normes égales .
![]()
Soit une f une fonction réelle d'une variable réelle .
A tout élément x de son domaine correspond un
réel y et un seul et on
écrit y = f(x) .
Ainsi le couple (x , f(x)) peut être
représenté dans le repère précédemment défini par un point M .
Donc lorsque
x décrit dom(f) , y décrit un sous ensemble de R et le point M décrit
une certaine courbe dans le repère . Cette courbe sera appelée représentation
graphique (ou courbe représentative) de f dans le repère considéré .
En
vue de la représentation graphique de f , on aura besoin d'établir son tableau
de variations qui n'est qu'un tableau à double entrée , dans lequel on prendra
sur les colonnes des valeurs assignées à la variable x et sur la ligne ,
les images correspondantes .
Les valeurs qu'on assigne à la variable x sont généralement choisies en
fonction de leur pertinence au regard de l'étude faite sur la fonction ; par
exemple on retiendra les valeurs de x qui annulent f ou qui la rend maximale
ou minimale .
Dans
un repère orthogonal , la fonction réelle d'une variable réelle f admet pour
axe de symétrie l'axe y'y des ordonnées si pour tout x appartenant à dom(f) ,
f(x) = f(-x) .
De plus f sera dite fonction paire .
Dans un repère normé , elle admet pour centre de symétrie l'origine O du
repère si f(-x) = -f(x) . De plus f sera dite fonction impaire .
Méthodologie
pour l'étude d'une fonction réelle d'une variable réelle f :
1) On détermine d'abord le domaine de définition de f ;
2) on vérifie ensuite sa monotonie et , le cas échéant , on vérifie si elle
est maximale ou minimale sur son domaine de définition et on détermine dans ce
cas le maximum ou le minimum ;
3) on détermine ensuite les valeurs de x pertinentes au regard de l'étude de f
(les valeurs qui annulent f , les valeurs pour lesquelles f est maximum ou minimum , etc) ;
4) on vérifie si la courbe représentative de f admet l'axe des ordonnées pour
axe de
symétrie (repère orthogonal ou orthonormé) ou l'origine O pour centre de symétrie (repère normé ou orthonormé) ; autrement dit on vérifie si f est paire ou
impaire .
5) enfin on trace à l'aide des résultats obtenus précédemment sa courbe
représentative .
1ère application
Soient les fonctions suivantes :
![]()

Détermine dom(f) et dom(g) .
2ème application
On donne la fonction numérique f suivante :
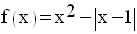
Étudie f sur l'intervalle [ – 2 , 2] et trace sa courbe représentative dans un repère orthonormé .
3ème application


NB : tu prendras dans les deux cas comme
repère un repère orthonormal.
4ème application
Étudie sur l'intervalle [– 3 , 3] la fonction f définie par :
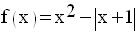
Représente
graphiquement f dans un repère orthonormal.
puissances d'un nombre et géométrie
(groupe ciblé : seconde)
1) Trouve un procédé géométrique pour construire le segment [AB] de longueur :
![]()
Calcule les réels x et y pour satisfaire l'égalité suivante :
![]()
2) On te donne un triangle rectangle (ABC)
rectangle en A . Soit (AH) la hauteur relative à l'hypoténuse .
Démontre la similitude des triangles (ABH) et (ACH) et en déduis que
AH2 = HB.HC
On donne un repère orthonormal d'axes x'Ox et y'Oy'
L'unité de mesure des longueurs
pris dans ce repère est le centimètre.
Soient les
points A (1 ; 0) et M (0 ; a), a étant un réel strictement positif .
Soient les points P , Q , R ; P appartient à x'x et (MP) est perpendiculaire à
(AM) , Q appartient à y'y et (PQ) est perpendiculaire à (MP) , R appartient à
x'x et (QR) est perpendiculaire à (PQ) .
Détermine les abscisses des points P
et R ainsi que l'ordonnée de Q .
Que peux-tu en déduire pour |xP | ; |yQ | ; |xR
| ?
On te donne en centimètres :
![]()
Que valent alors |xP | ; |yQ
| ; |xR | ?
Trouve un procédé géométrique
pour placer les points A , P , Q , R .
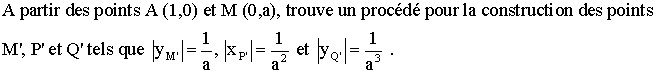
parallélogramme et extremum d'une parabole
(groupes ciblés : seconde et première S)
Que doivent vérifier les réels positifs a , b ,
c pour que le triangle (ABC) tel que
AB = c , BC = a et AC = b soit constructible ?
Soit un point quelconque M appartenant à [AB] et
tel que AM = x .
Quel est le domaine de définition de x ?
Soit h la mesure géométrique de la hauteur [AH]
relative
au côté [BC] .
Mène de M une parallèle à (BC) qui rencontre (AC) en N .
Mène de N une parallèle à (AB) qui rencontre (BC) en P .
Quelle est la nature du quadrilatère (MNPB) ?
Détermine la valeur que doit prendre x pour que l'aire de ce quadrilatère soit
maximale .
La suite de l'exercice est dédiée aux lycéens de première S
Pour la suite de l'exercice tu prendras a = 6 cm
, b = 5 cm
et c = 7 cm .
Calcule la mesure géométrique h de la hauteur [AH] .
![]()
l'aire f(x) du quadrilatère (MNPB) .
L'unité prise sur les deux axes du
repère est le centimètre .
On te donne un point Q de (C) tel que xQ = 4 .
Détermine la tangente (d) à (C) au point Q .
Trouve l'équation de la droite (d') passant par Q et faisant avec (d) un angle
(d , d') égal en valeur absolue à 30° .
![]()
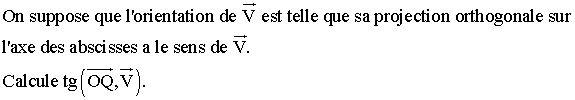
système d'inéquations du premier degré et
étude des angles intérieurs d'un triangle
(groupe ciblé : seconde)
On te donne un triangle quelconque (ABC) dont les
mesures en degré de ses angles intérieurs sont :
a pour l'angle au sommet A ; b pour l'angle au sommet B et c pour l'angle au
sommet C .
De plus tu supposeras :
![]()
Sachant que a + b + c = 180° et que c se déduit
de a et b , tu t'intéresseras uniquement à l'étude de a et b .
Trouve les six conditions que doit vérifier le couple (a ; b) .
Résous graphiquement le système qui découle de
ces six conditions .
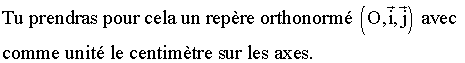
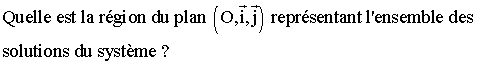
Quel est l'ensemble de points (a ; b) pour lequel le triangle (ABC) n'existe pas ?
Quel est l'ensemble des points (a ; b) pour lequel le triangle (ABC) est isocèle ? équilatéral ? rectangle ? rectangle isocèle ?

droites et plans parallèles
(groupe ciblé : première S)
Rappel des définitions et des théorèmes
Axiome d'Euclide : Existence et unicité de la parallèle à une droite menée d'un point ne lui appartenant pas .
Théorème 1 : Si deux droites sont parallèles, tout plan coupant l'une coupe l'autre .
Théorème 2 : Deux droites x et y parallèles à une même troisième z sont parallèles entre elles .
Théorème 3 et ses conséquences : Deux angles
qui ont les côtés respectivement parallèles et de même sens sont
isométriques.
Deux angles qui ont leurs côtés respectivement parallèles et de sens
contraires sont isométriques .
Deux angles qui ont deux côtés parallèles et de même sens, et les deux
autres parallèles et de sens contraires sont supplémentaires (la somme de
leurs mesures vaut 180°) .
Définition 1 : On appelle angle de deux droites (d) et (d') que l'on note (d ; d'), l'un des angles formés par les parallèles menées d'un point quelconque A de l'espace à ces deux droites . Si l'un de ces angles est droit, alors on dira que (d) et (d') sont orthogonales .
Définition 2 : Une droite (d) et un plan P sont parallèles lorsqu'ils n'ont aucun point commun .
Théorème 4 et ses corollaires : Pour qu'une
droite (d), non contenue dans un plan P, soit parallèle à P, il faut et il
suffit qu'elle soit parallèle à une droite de ce plan .
Lorsqu'une droite (d) est parallèle à un plan P, elle est parallèle à
l'intersection de ce plan avec tout plan Q contenant (d) .
Lorsqu'une droite (d) est parallèle à un plan P, toute parallèle (AB) à (d)
menée d'un point quelconque A de P est contenue dans P .
Théorème 5 : Toute droite parallèle à deux plans sécants est parallèle à leur intersection .
Théorème 6 : Lorsque deux plans sécants P et Q contiennent respectivement deux droites parallèles (y) et (z), leur intersection (d) est parallèle à (y) et à (z) .
Théorème 7 : Par un point donné de l'espace, on peut mener un plan et un seul parallèle à deux droites données non parallèles .
Théorème 8 : Par une droite (d) donnée de l'espace, on peut mener un plan et un seul parallèle à une droite donnée (d') non coplanaire avec (d) .
Définition 3 : Deux plans sont dits parallèles lorsqu'ils n'ont aucun point commun .
Théorème 9 et son corollaire : Pour que deux
plans de l'espace soient parallèles il faut et il suffit que l'un d'eux
contienne deux droites concourantes parallèles
à l'autre .
Deux plans de l'espace sont parallèles lorsque l'un d'eux contient deux droites
concourantes respectivement parallèles à deux droites concourantes de l'autre
.
Théorème 10 et ses corollaires : Par un point
donné A de l'espace, n'appartenant pas à un plan P, on peut mener un plan Q
parallèle à P et un seul .
Deux plans parallèles à un même troisième sont parallèles entre eux .
Lorsque deux plans de l'espace sont parallèles, tout plan qui rencontre l'un
d'eux rencontre aussi l'autre et les deux droites d'intersection sont
parallèles .
Théorème 11 et ses corollaires : L'ensemble des
droites parallèles à un plan P, menées d'un point donné A n'appartenant à
P, est le plan Q passant par A et parallèle à P .
Lorsque deux plans sont parallèles, toute droite qui coupe l'un coupe l'autre;
toute droite parallèle à l'un est parallèle à l'autre .
Théorème 12 : Deux plans parallèles découpent
sur deux droites parallèles des
segments isométriques .
Théorème 13 et sa réciproque : Trois plans parallèles
découpent sur deux droites
qui leur sont sécantes , quelconques, des segments dont les mesures
géométriques sont
proportionnelles . Réciproquement, si trois droites (AA') , (BB') et (CC')
découpent
sur deux droites (d) et (d') non coplanaires des segments dont les
mesures géométriques
sont proportionnelles, ces trois droites sont
contenues dans des plans parallèles .
la géométrie analytique dans l'espace
(groupe ciblé : première S)
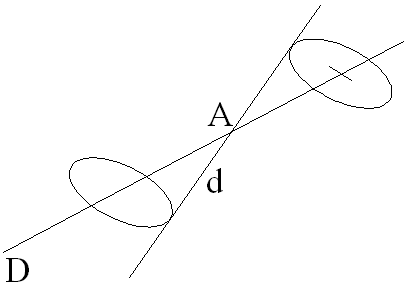
1- Base et repère de l’espace – Vecteurs dans un repère de l’espace


On note :
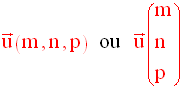
Propriétés
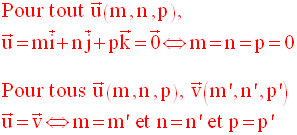
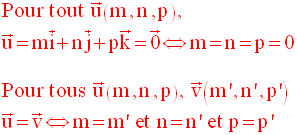
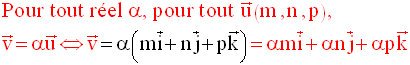
Soit O un point quelconque de cet espace.
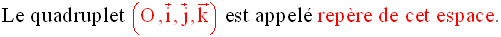
Ce repère possède un des deux sens : direct ou indirect.


Lorsque le repère est donné
sans aucune indication quant à sons sens,
ce dernier est
supposé direct.
Trois types de repère peuvent se présenter à
nous :
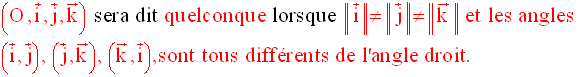
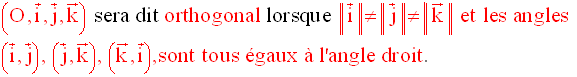

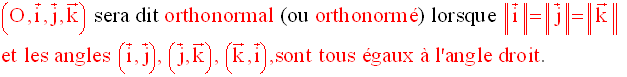
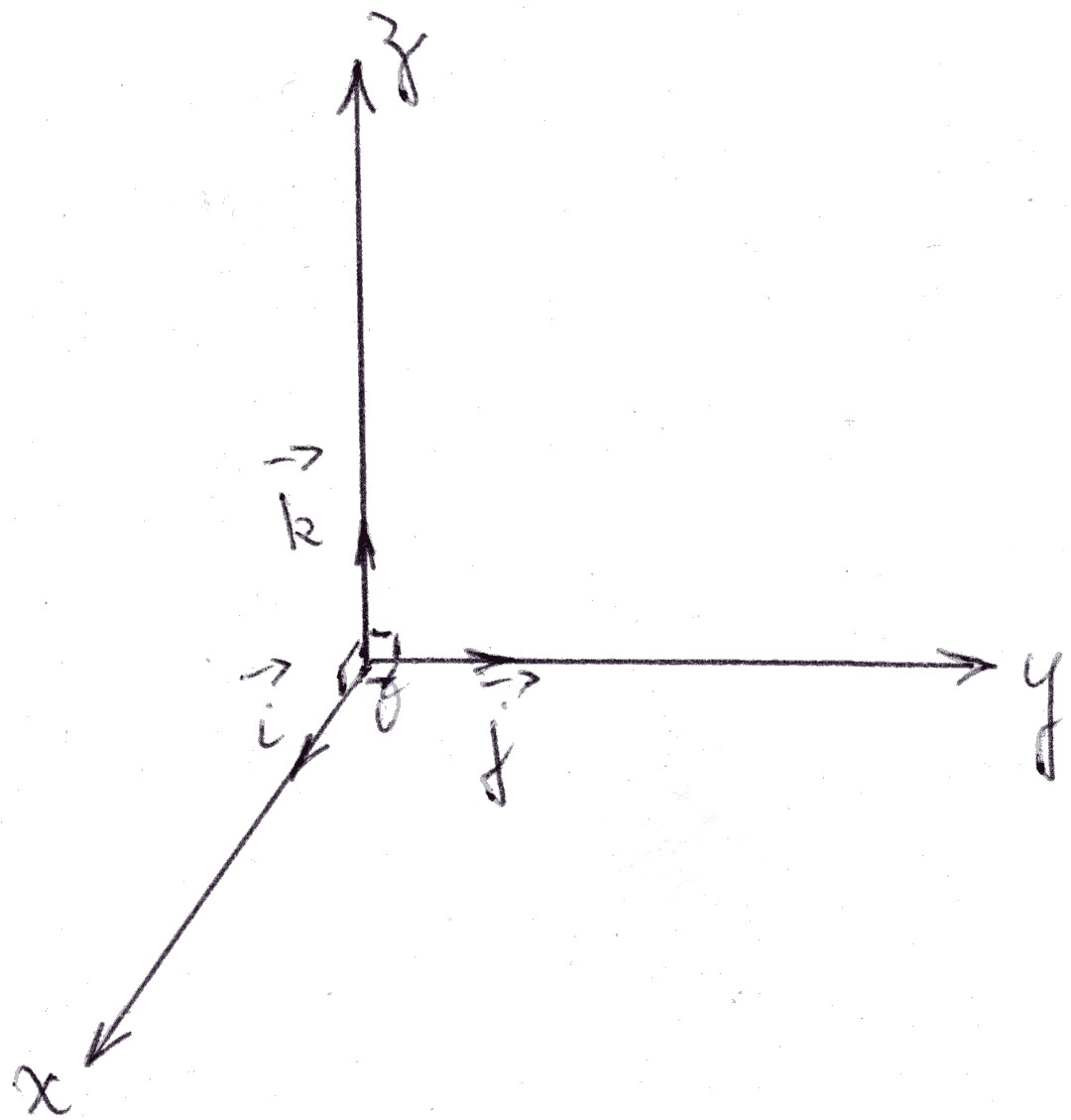
Repère orthonormal
Remarques
Toute propriété satisfaite dans un repère quelconque l’est également dans tout repère particulier.
Si la nature du repère n’est pas explicitement précisée, alors on considèrera qu’il est un repère direct et quelconque.



Dans ce repère, on retrouve les mêmes propriétés citées en début de ce chapitre :

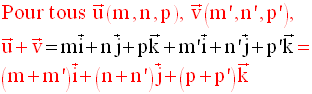
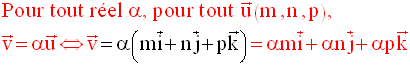
Soient, dans ce repère, deux points quelconques et distincts A(x,y,z) et B(x’,y’,z’).
D’après la relation de Chasles, on peut écrire :
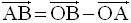
Or,
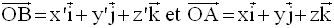
Par conséquent,
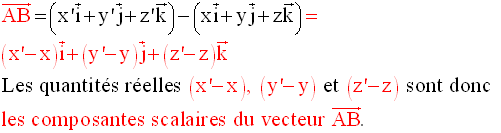
La
première composante est la différence
entre l’abscisse de l’extrémité
du vecteur
considéré et celle de son
origine.
La
seconde composante est la différence entre
l’ordonnée de l’extrémité
du vecteur
considéré et celle de son
origine.
La
troisième composante est la différence
entre la cote de l’extrémité
du vecteur
considéré et celle de son
origine.
2- Parallélisme

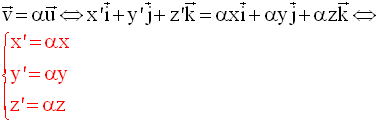
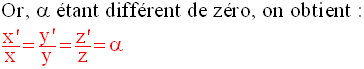
Dans un repère, deux vecteurs non nuls ont leurs directions ou supports parallèles si et seulement si leurs composantes scalaires de même nom sont proportionnelles.
Ce théorème est logiquement équivalent au suivant :
Dans un repère,
deux vecteurs non nuls sont colinéaires si et seulement si
leurs
composantes scalaires de même nom sont proportionnelles.

d // d’
3- Vecteurs orthogonaux - Produit scalaire

Il est évident que si deux vecteurs sont orthogonaux, alors deux vecteurs qui leur sont respectivement colinéaires sont également orthogonaux.

d et d’ sont orthogonales
Produit scalaire

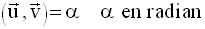
Propriétés
1-
Comme la multiplication dans
R, ensemble des nombres réels, est commutative
et
comme deux angles orientés opposés ont même cosinus,
il est alors évident que le
produit scalaire des vecteurs est également commutatif.
On écrit :
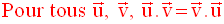
2-

3-

Théorème
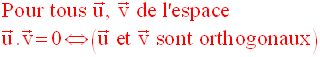
Démonstration
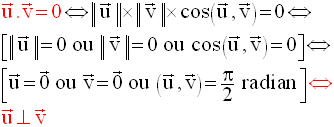
Expression analytique du produit scalaire dans un repère de l’espace
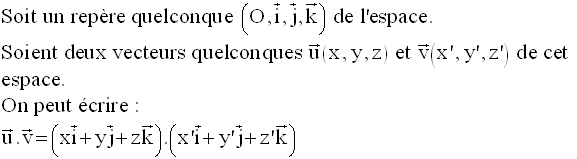

C’est
l’expression analytique générale du produit scalaire de deux vecteurs de
l’espace
muni d’un repère quelconque.
Si le repère est normal, avec :
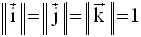
alors,
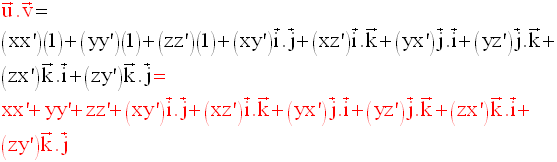
Si le repère est orthogonal, alors :
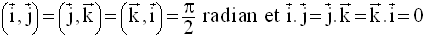
De plus, sachant que le produit scalaire est commutatif, l’expression devient :
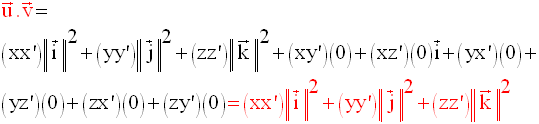
Si le repère est orthonormal, alors :
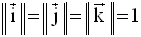
et
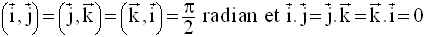
Dans ces conditions, l’expression analytique du produit scalaire se réduit à :
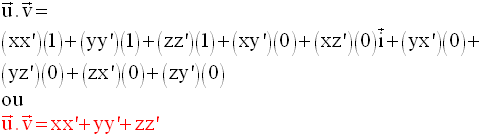
D’après ce qui a été dit et démontré précédemment, on a le théorème important suivant :
Dans l’espace muni
d’un repère orthonormal, deux vecteurs sont orthogonaux
si et
seulement si l’expression analytique de leur produit scalaire est nulle.
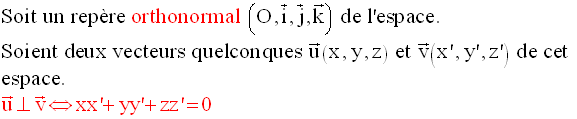
Une application directe du produit scalaire dans l’espace muni d’un repère orthonormal

Si de plus, ce vecteur est différent du vecteur nul, alors :
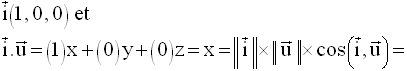
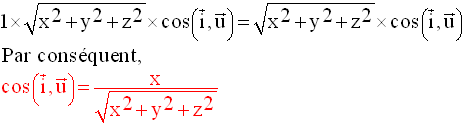
De la même manière, on établit les deux autres relations :
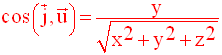
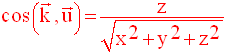

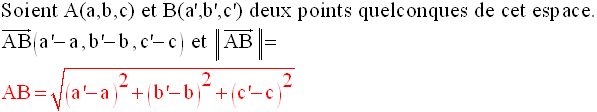
Cette relation est l’expression analytique du théorème de Pythagore.
Dans un repère
orthonormal de l’espace, le produit scalaire
permet ainsi de calculer
la distance entre deux points ou encore la
longueur d’un segment de cet espace.
4- Equations de la droite, du plan et de quelques figures ou solides remarquables de l’espace muni d’un repère orthonormal
Equation d’un plan
passant par un point donné et orthogonal à un vecteur non
nul donné



Démonstration

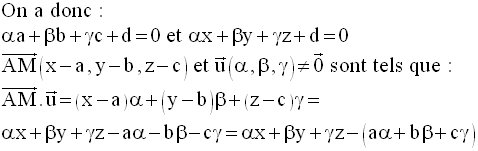
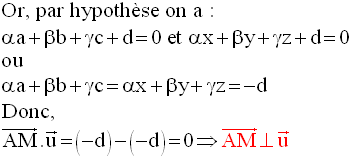

Conclusion :
Dans l’espace muni
d’un repère orthonormal, l’équation d’un plan est de la forme
générale :


Coordonnées des points d’intersection d’un plan avec les trois axes
du repère
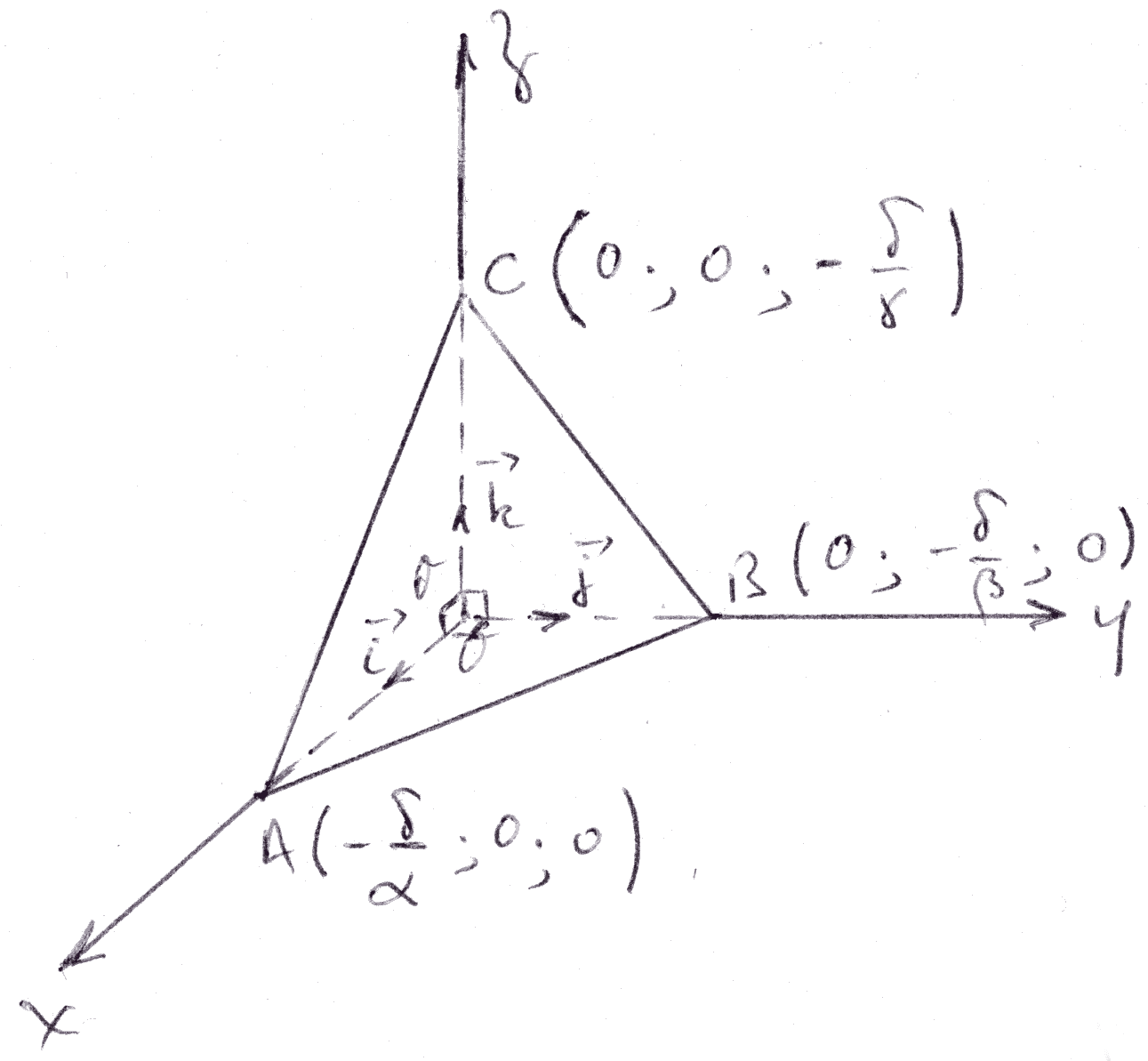

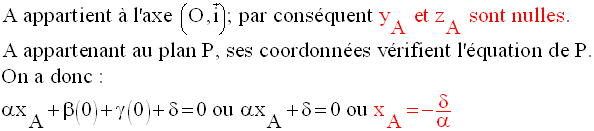
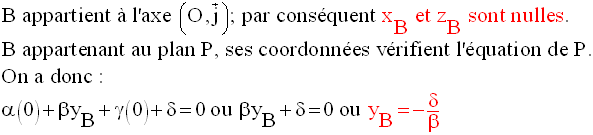
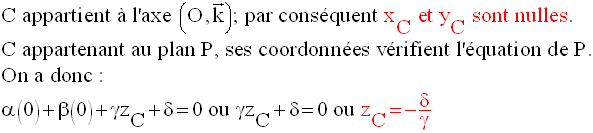
Parallélisme et orthogonalité de deux plans
Théorème
Dans l’espace, muni d’un repère orthonormal, deux plans distincts sont parallèles si seulement si deux de leurs vecteurs normaux respectifs sont colinéaires.
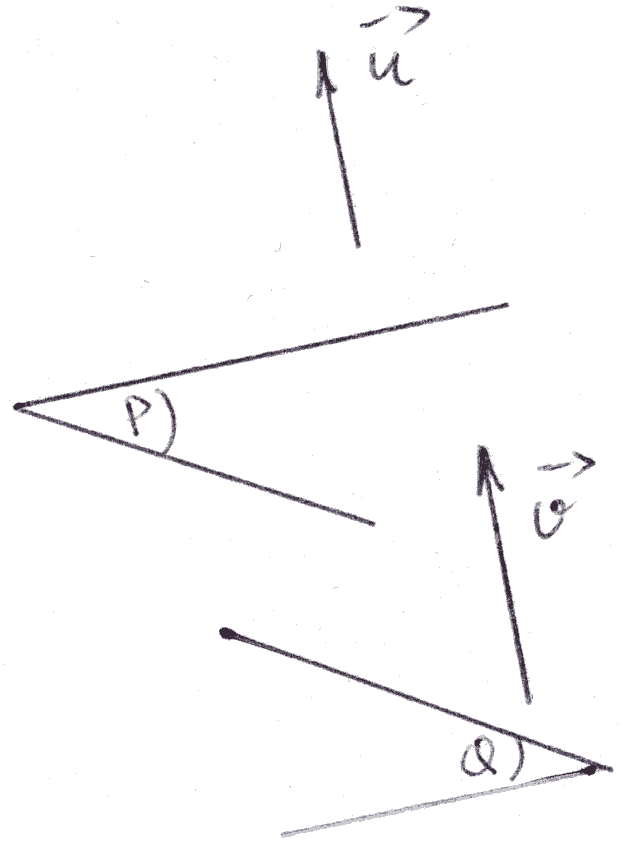
Démonstration

On suppose que P et Q sont parallèles et on démontre que leurs vecteurs normaux respectifs :
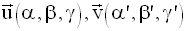
sont colinéaires.
P et Q étant parallèles, toute droite orthogonale à l’un est orthogonale à l’autre.

Réciproque
On suppose que P et Q sont tels que :
On démontre que P et Q sont parallèles.
Les deux vecteurs précités étant colinéaires, ont même direction.
P et Q étant orthogonaux à
ces deux vecteurs, sont orthogonaux à cette direction, donc
ils sont parallèles.
Conséquence

Si de plus α, β et γ sont différents de 0, alors cette condition nécessaire et suffisante peut s’écrire :

Cette conséquence sert souvent à démontrer le parallélisme de deux plans inclus dans un espace muni d’un repère orthonormal.
Remarque :

Théorème
Dans l’espace,
muni d’un repère orthonormal, deux plans distincts sont orthogonaux
si seulement si deux de leurs vecteurs normaux respectifs sont
orthogonaux.
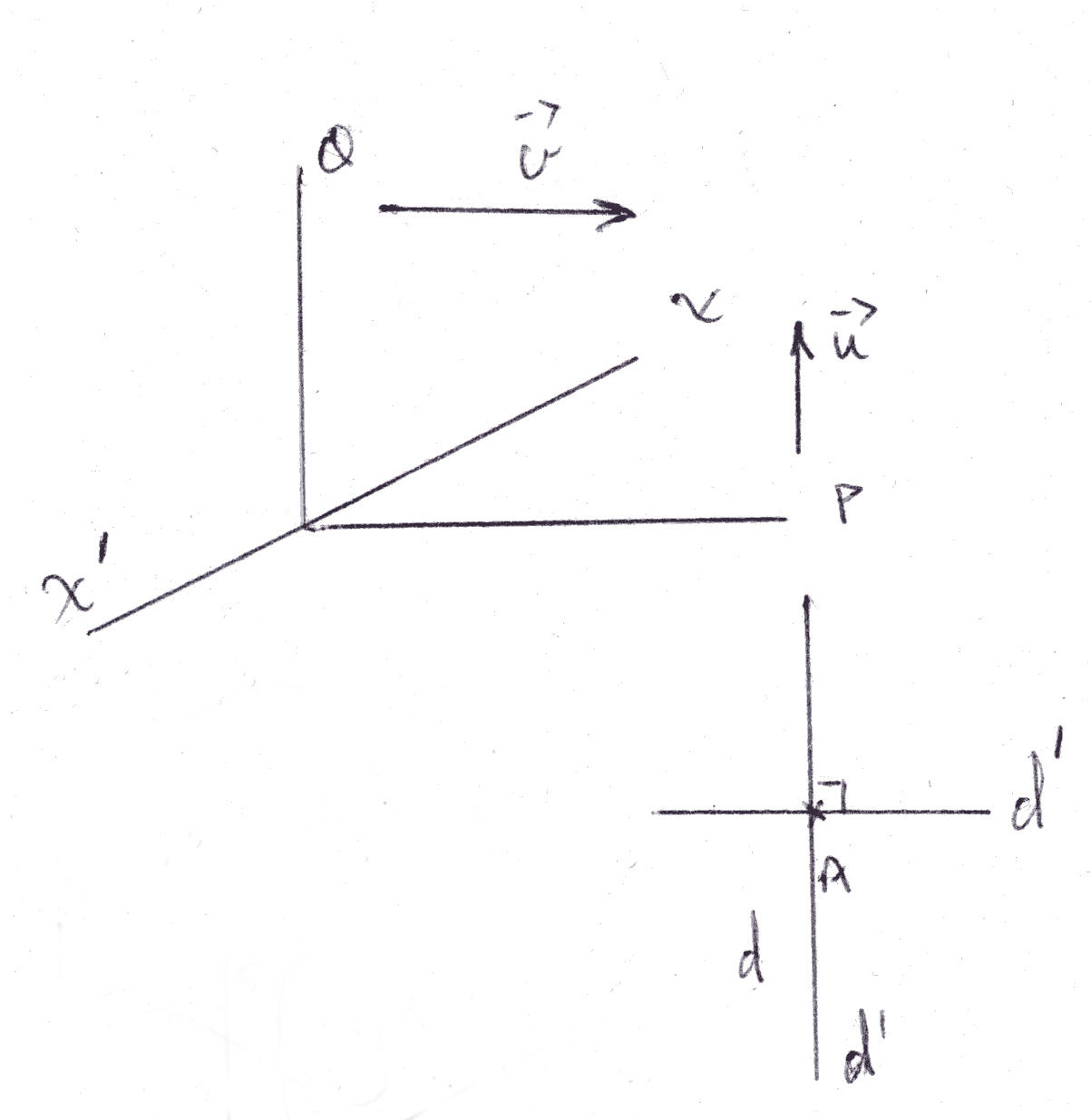
Démonstration

Les vecteurs :
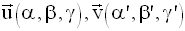
leur sont respectivement normaux.
On suppose que P et Q sont orthogonaux et on démontre que ces deux vecteurs sont orthogonaux.
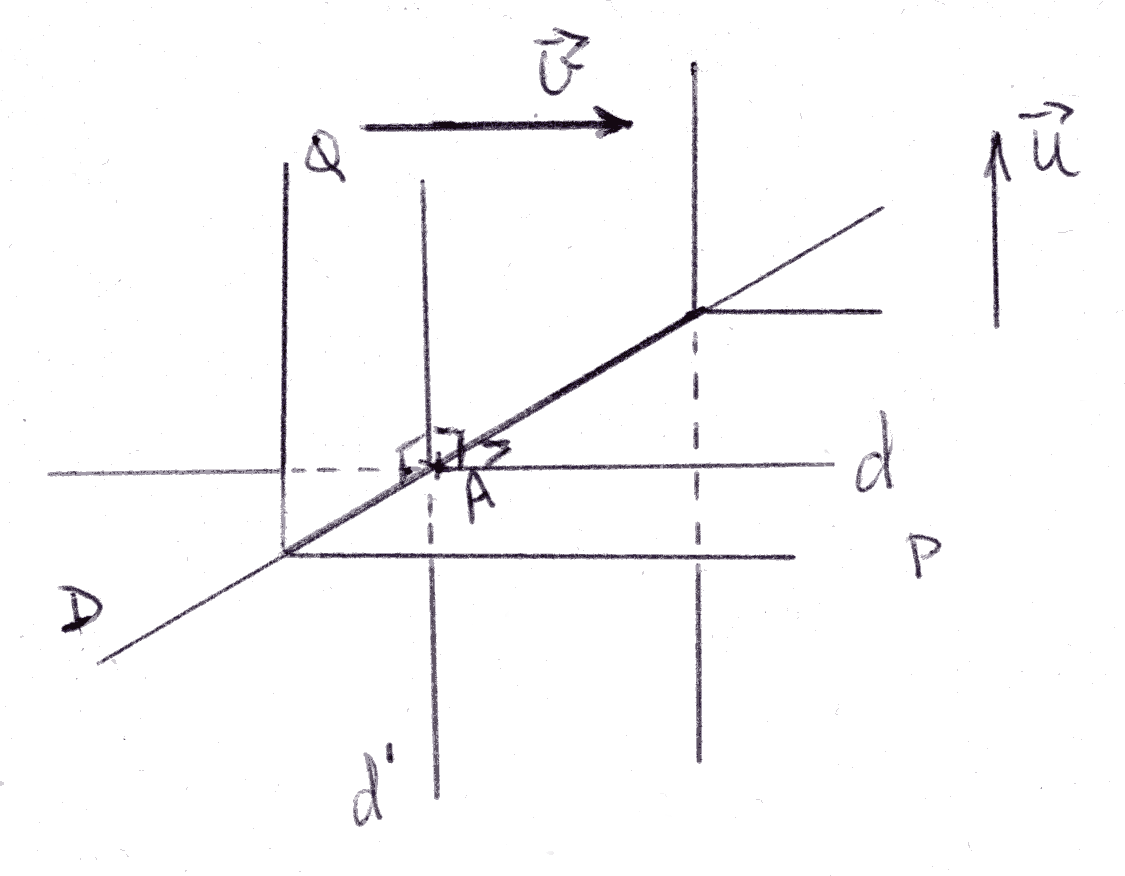
P et Q étant distincts, se coupent selon la droite D.
Soit A un point quelconque de D.
Dans P, on élève de A une
droite d perpendiculaire à D. Dans Q, on élève de A une droite
d’ perpendiculaire à D.
P et Q étant orthogonaux, l’angle dièdre (d, d’) est droit.
d et d’ sont donc respectivement orthogonales à Q et à P.


Réciproque
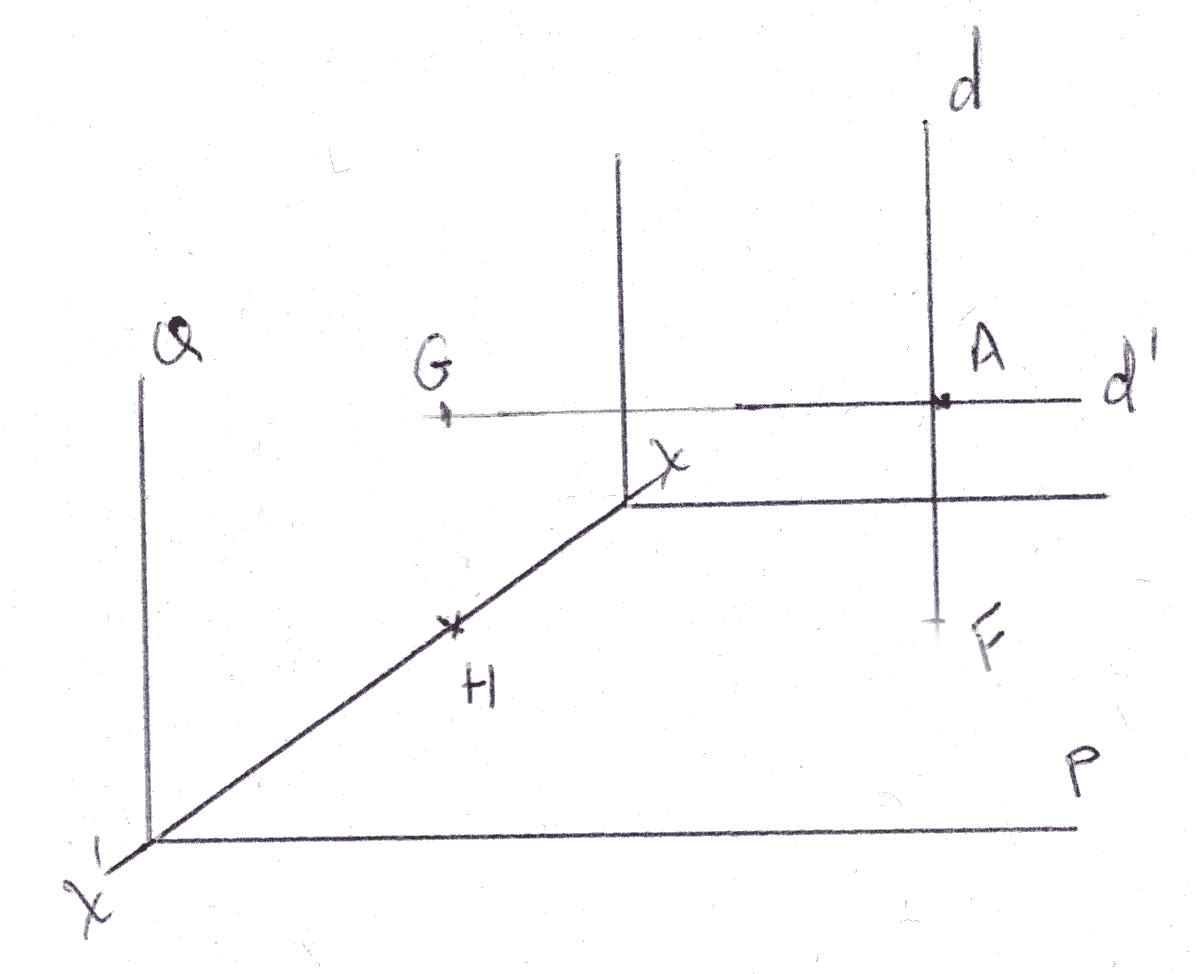
On suppose que P et Q sont tels que :
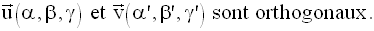
On démontre que P et Q sont orthogonaux.

L’angle (d,d’) est droit.
Soit (xx’) l’intersection des plans P et Q.
Le plan (d,d’) rencontre (xx’) au point H.
La droite d rencontre P au point F et la droite d’ rencontre Q au point G.
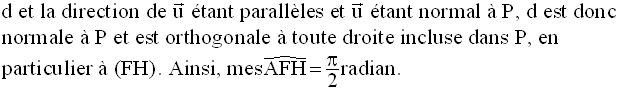
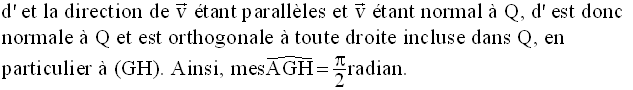
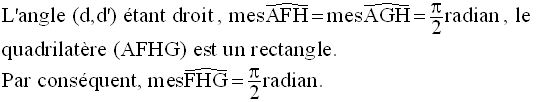
(HF) étant parallèle à d’ et d’ étant orthogonale à Q, (HF) l’est également ; par conséquent (HF) est orthogonale à toute droite de Q et en particulier à (x’x) ; de même, (HG) étant parallèle à d et d étant orthogonale à P, (HG) l’est également ; par conséquent (HG) est orthogonale à toute droite de P et en particulier à (x’x).

Par conséquent P et Q sont orthogonaux.
Conséquence
Soient, dans un espace muni d’un repère orthonormal, deux plans définis comme suit :
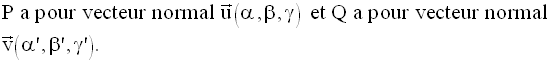

Cette conséquence sert souvent à démontrer l’orthogonalité de deux plans inclus dans un espace muni d’un repère orthonormal.
Plan passant par trois points, deux à deux distincts, non alignés, donnés
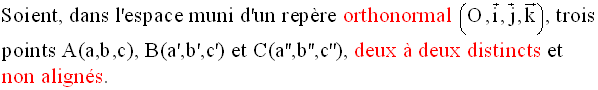
On sait que de tels points définissent entièrement un plan que l’on désigne par P.
Connaissant les coordonnées
de ces points, il s’agit de trouver l’équation cartésienne
(E) de P dont la forme générale est :
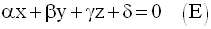
Chacun de ces trois points appartenant à P a ses coordonnées vérifiant (E).
On obtient ainsi un système de trois équations à quatre inconnues :
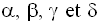
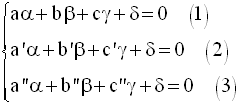
En prenant ces équations deux à deux, et en soustrayant membre à membre, on élimine δ.
(1) et (2) donnent :
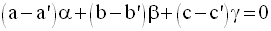
(1) et (3) donnent :
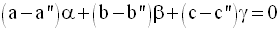
(2) et (3) donnent
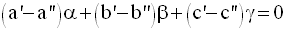
Finalement, on obtient un système de trois équations à trois inconnues α, β et γ :
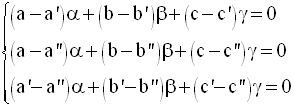
Comme trois points deux à
deux distincts et non alignés déterminent un plan, ce système
doit admettre au moins une solution.
Par ailleurs, le déterminant de Cramer étant nul, il admet donc une infinité de solutions.
On fixe donc une des
inconnues, par exemple α, en la supposant différente de
zéro et on
calcule les deux autres, β et γ, en fonction de α.
Pour déterminer δ en fonction de α, il suffit d’utiliser une des trois équations (1), (2) et (3).
Revenant à la forme générale
de l’équation (E), et en remplaçant les trois inconnues
calculées en fonction de α, on obtient une équation de la forme :
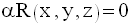
Comme α est non nulle, on peut simplifier et ainsi obtenir l’équation recherchée :
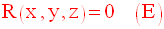
Exemple
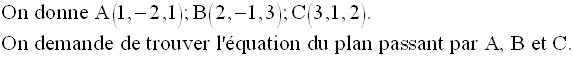
Ces trois points étant deux
à deux distincts et non alignés définissent donc un plan.
Soit P ce plan.
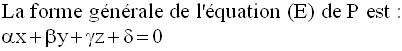
A, B et C appartenant à P,
leurs coordonnées respectives doivent vérifier cette
équation ; on a donc :
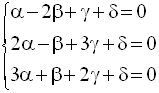
En soustrayant les deux membres des deux premières équations, on obtient :
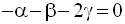
En soustrayant les deux membres des deux dernières équations, on obtient :

En soustrayant les deux membres de la première et troisième équation, on obtient :
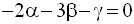
On obtient finalement le système :
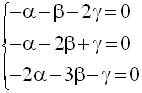
Ce système dont le
discriminant de Cramer est nul, admet une infinité de solutions,
du fait que le plan P existe.
On fixe la composante α en la supposant non nulle.
Les deux dernières équations
donnent, par addition membre à membre, une relation
entre α et β :
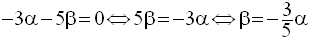
La première équation donne γ en fonction de α et β :
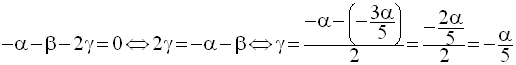
La première équation du premier système donne :
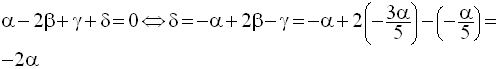
(E) devient :
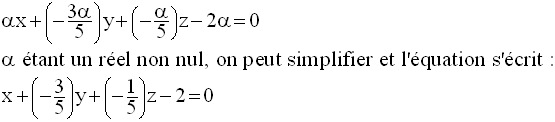
D’où l’équation de P :
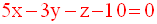
Plan passant par un point donné et orthogonal à une droite donnée
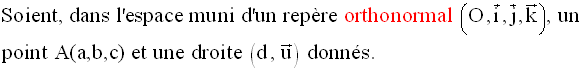
On demande de trouver l’équation (E) du plan P passant par A et orthogonale à d.
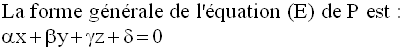

A appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans
(E), x, y
et z par ces coordonnées, on déduit δ.
Exemple
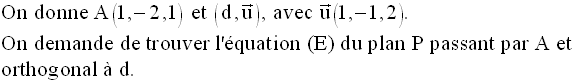


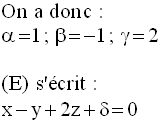
A appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans (E), x,
y et z par ces coordonnées, on déduit δ.
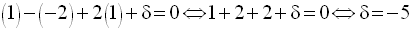
L’équation (E) est finalement :

Plan passant par deux
points distincts donnés et parallèle à une droite donnée,
les deux points étant tels que la droite qu’ils définissent et celle donnée sont
non coplanaires
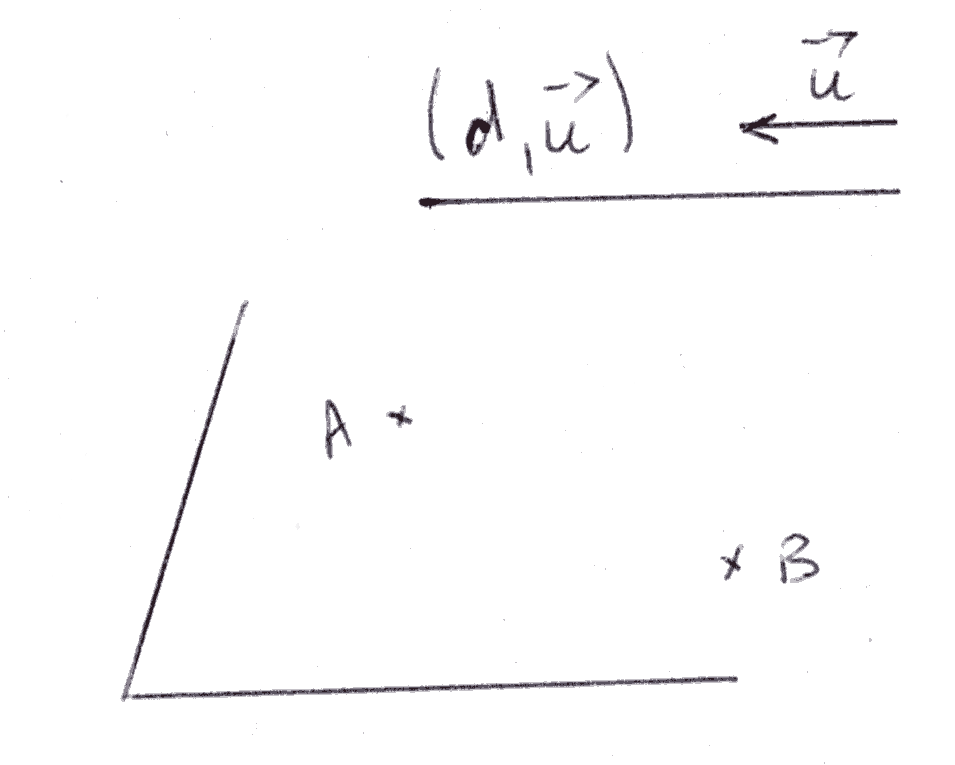

On demande de trouver l’équation (E) du plan P contenant [AB] et parallèle à d.
Un de ses vecteurs normaux est :
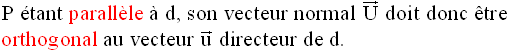
On a donc :
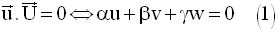
A appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans (E), x,
y et z par ces coordonnées, on obtient :
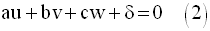
B appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans (E), x,
y et z par ces coordonnées, on obtient :
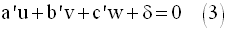

On obtient ainsi un système de quatre équations à quatre inconnues u, v, w et δ.
Son discriminant étant nul, il admet donc une infinité de solutions.
En fixant une des quatre
inconnues, par exemple u, et en la supposant non nulle,
on
calcule les trois autres en fonction de celle-ci.
Revenant à la forme générale
de l’équation (E), et en remplaçant les trois inconnues
calculées en fonction de u, on obtient une équation de la forme :
Comme u est non nulle, on peut simplifier et ainsi obtenir l’équation recherchée :
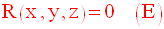
Exemple
Trouve l’équation du plan P
passant par les points A(1,1,1) et B(2,3,4) et parallèle
à l’axe des cotes z’z.
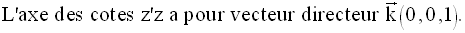
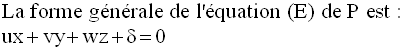
Un de ses vecteurs normaux est :
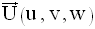
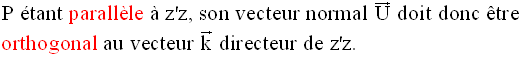
On a donc :
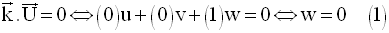
A appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans (E), x,
y et z par ces coordonnées, on obtient :
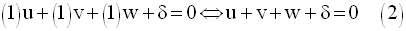
B appartenant à P, ses
coordonnées doivent vérifier (E) ; en remplaçant dans (E), x,
y et z par ces coordonnées, on obtient :
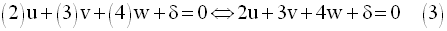

D’où le système :
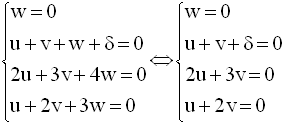
Le discriminant de Cramer du système étant nul, ce dernier admet une infinité de solutions.
En fixant la composante u, supposée non nulle, on calcule δ et v en fonction de celle-ci.
Les deux dernières équations permettent de calculer v en fonction de u ; on obtient :
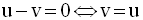
La deuxième équation permet de calculer δ en fonction de u ; on obtient :
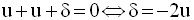
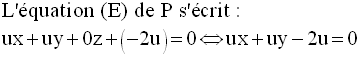
En simplifiant par u, non nulle, on obtient finalement :
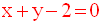
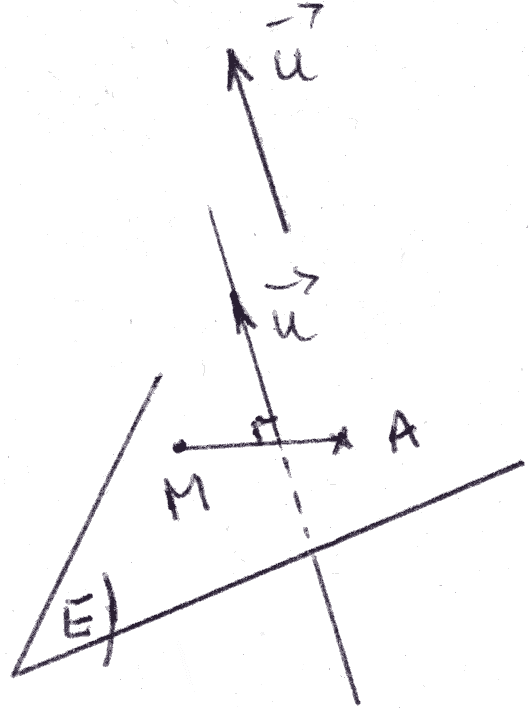
Distance d’un point à un plan

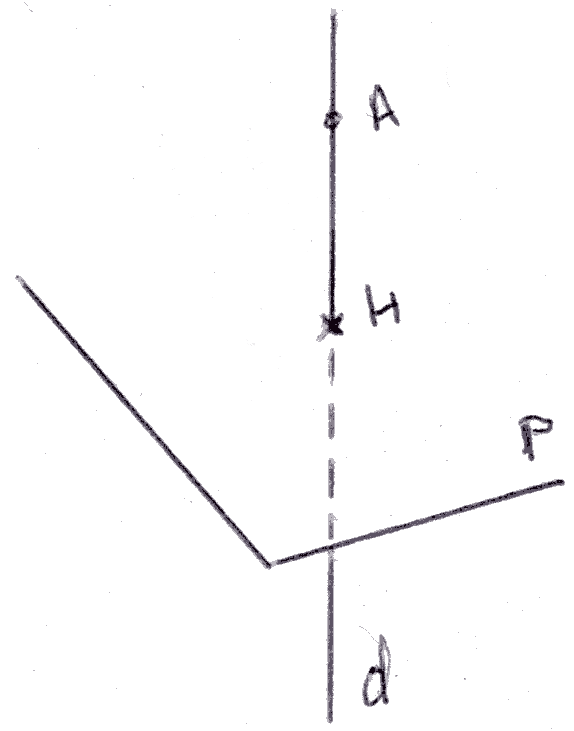
On abaisse de A la droite d orthogonale à P qui rencontre ce dernier au point H.
Par définition, AH est la distance du point A au plan P.

On a donc :
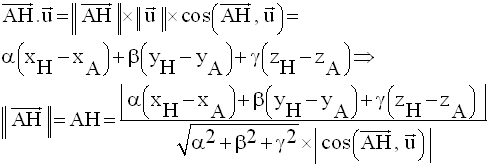
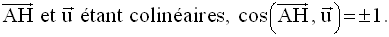
Donc,
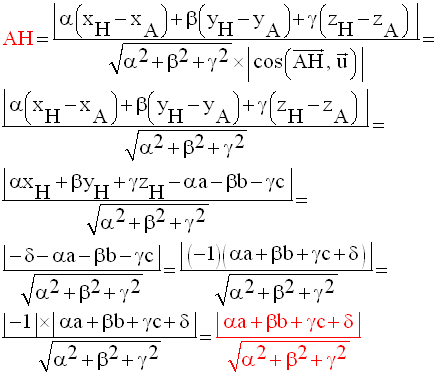
Equations d’une droite
dont un des vecteurs directeurs est donné et passant par
un point donné
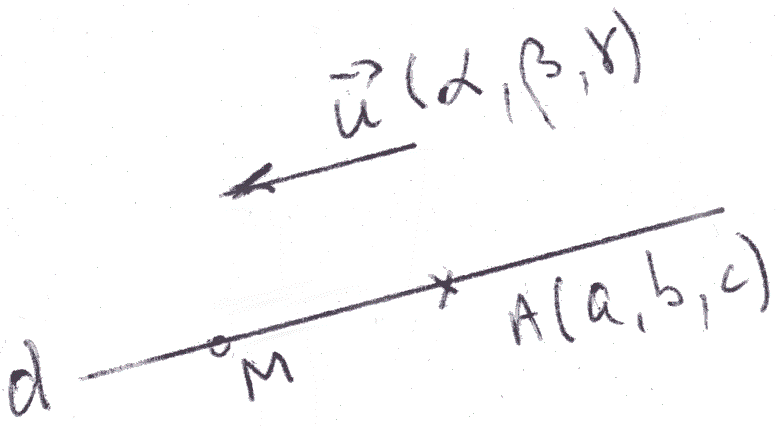
Un point M(x,y,z) de cet
espace appartient à d si et seulement s’il existe un réel
λ et un seul tel que :
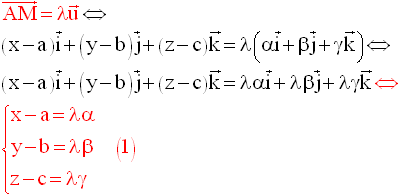
Ce sont là les équations paramétriques de la droite d.
Si de plus d n’est parallèle
à aucun des axes du repère et n’est confondue avec aucun
de ces axes, alors cette condition nécessaire et suffisante s’écrit sous la
forme d’une
situation de proportionnalité :
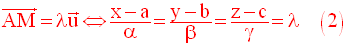
Réciproquement, tout système de la forme :
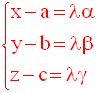
définit les
équations paramétriques d’une droite passant par le point de coordonnées a,
b et c et ayant pour vecteur directeur de composantes scalaires α, β et γ.
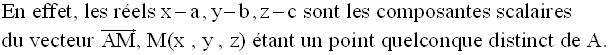
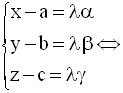
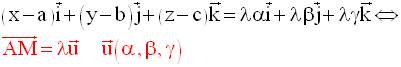

Pour tout point M(x , y, z) de la droite d, il existe un réel λ et un seul tel que :
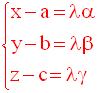
Réciproquement, pour tout réel λ, le système :
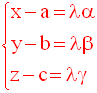
définit un point M(x , y, z) unique appartenant à la droite d.
Lorsque le paramètre réel λ parcourt l’ensemble des nombres réels, le point M(x , y , z) parcourt la droite d.
Intersection de deux plans
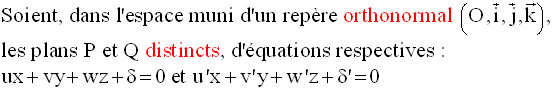
On sait que s’il existe au moins un réel non nul λ tel que :
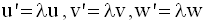
alors P et Q sont parallèles.
Dans le cas contraire,
c’est-à-dire si les coefficients réels u, v et w ne sont pas
respectivement proportionnels aux coefficients réels u’, v’ et w’, alors
P et Q, étant
distincts, ne sont pas parallèles et se coupent selon
une droite d. d est ainsi
l’intersection de ces deux plans.
Tout
point M(x, y, z) appartenant à d appartient
simultanément à P et Q et
ses
coordonnées doivent vérifier le système de deux équations :
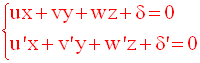
Réciproquement, tout système de deux équations de la forme :

et tel que les coefficients
réels u, v et w ne sont pas respectivement
proportionnels
aux coefficients réels u’, v’ et w’ représente une
droite qui est intersection des plans d’équations respectives :

Le système :
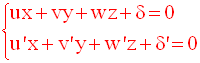
est appelé système d’équations représentant la droite d.
Passage du système
d’équations représentant une droite aux équations
paramétriques de cette droite
Une droite d est donnée par un système de deux équations de la forme :
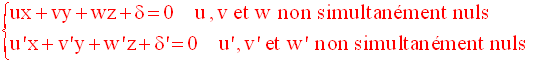
On se propose de trouver ses équations paramétriques.
On prend deux points
distincts A et B arbitraires tels que leurs coordonnées
respectives vérifient le système donné.
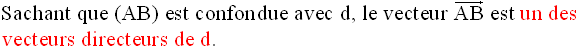
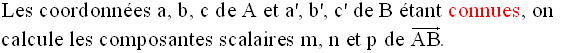
Pour tout point M(x, y, z) appartenant à d, il existe au moins un réel λ et un seul tel que :
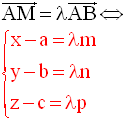
Si de plus m, n et p sont différents de 0, on peut écrire la situation de proportionnalité :
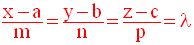
Exemple
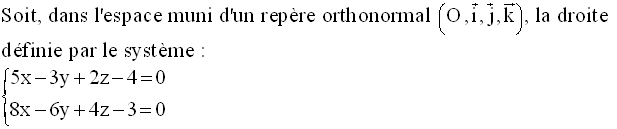
On demande de trouver les équations canoniques de cette droite.
Si l’on prend une valeur arbitraire pour x, par exemple 0, on constate que le système :
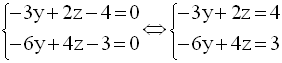
n’admet aucune solution.
On verra par la suite pourquoi on ne peut donner à x une valeur arbitraire.
Soit z égale à 0 ; le système devient :
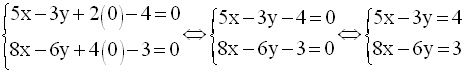
Le discriminant est égal à :

Ce discriminant étant différent de zéro, le système admet une solution unique dans R2.
Cette solution est :
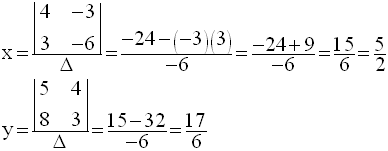
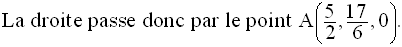
Soit y égale à 0 ; le système devient :
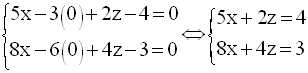
Le discriminant est égal à :
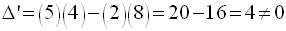
Ce discriminant étant différent de zéro, le système admet une solution unique dans R2.
Cette solution est :

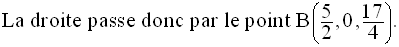
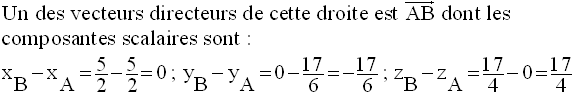
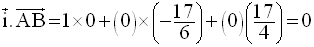

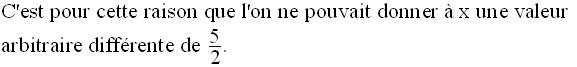
M(x , y, z) étant un point quelconque de cet espace, on a donc la suite des équivalences logiques suivante :
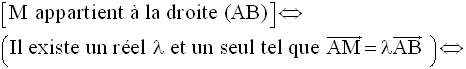

Parallélisme et orthogonalité de deux droites dont les équations sont données

d et d’ont pour vecteurs directeurs :
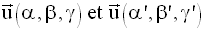
Théorème
d et d’ sont
parallèles si et seulement si les
directions ou supports de ces vecteurs
directeurs sont parallèles.
Ce qui se traduit par :
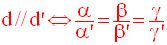
Théorème
d et d’ sont
orthogonales si et seulement si le produit
scalaire des mêmes vecteurs
directeurs est nul.
Ce qui se traduit par :
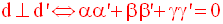
Distance d’un point à une droite dont les équations sont données
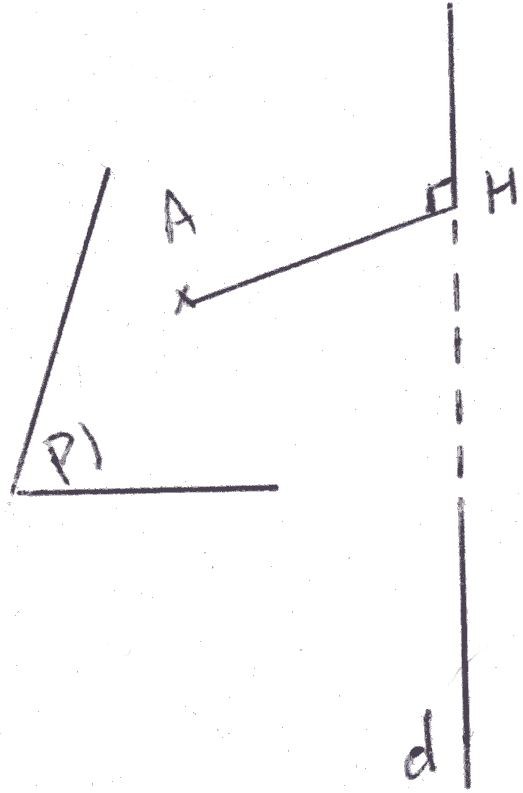

On demande de calculer la distance de A à d.
On mène de A le plan P orthogonale à d qui rencontre cette dernière au point H.
Comme d est orthogonale à P, elle est orthogonale à toute droite incluse dans P et en particulier à (AH).
Par définition, AH est la distance de A à d.
La méthode pour calculer AH
1- On cherche l’équation du plan P
2- On calcule les coordonnées de H
3- Connaissant les coordonnées de A et de H, on applique le théorème de Pythagore
Exemple
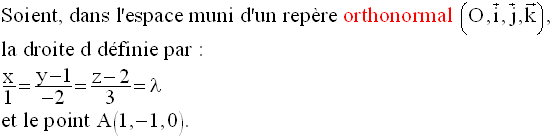
(L’unité de mesure des longueurs prise dans le repère est le centimètre)
On demande calculer la distance de A à d au dixième près par défaut.
On mène de A le plan P orthogonale à d qui rencontre cette dernière au point H.
Equation de P
La forme générale de l’équation de P est :
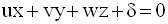
d étant orthogonale à P, tout vecteur directeur de d est un vecteur normal de P.
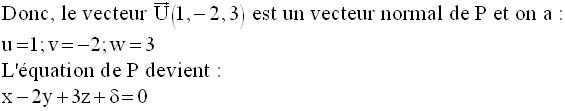
A appartenant à P, ses coordonnées vérifient donc l’équation de P et on a :
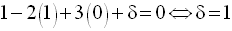
Finalement, l’équation de P est :
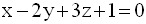
Coordonnées de H
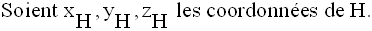
H étant l’intersection de d et de P, ses coordonnées vérifient le système :
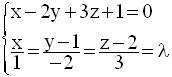
On a donc :
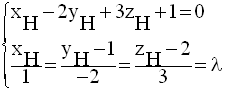
La situation de
proportionnalité permet de calculer l’ordonnée et la cote de H en
fonction de son abscisse ; on a :
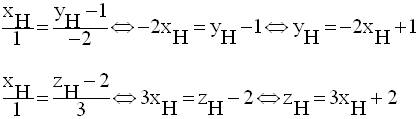
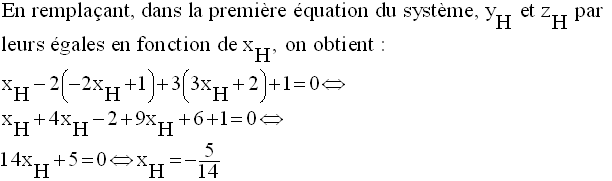
Par conséquent,
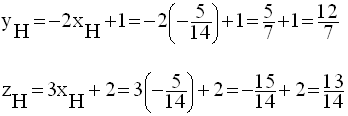
Calcul de AH
Le théorème de Pythagore appliqué dans cet espace donne :
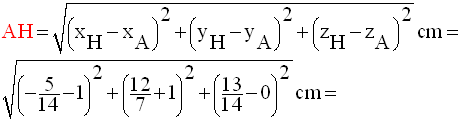
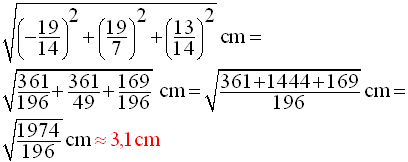
5- Coordonnées du barycentre d’un système de points pondérés de l’espace muni d’un repère orthonormal

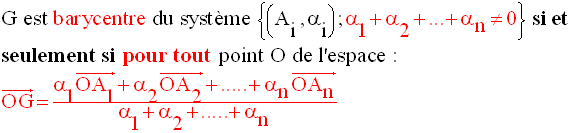
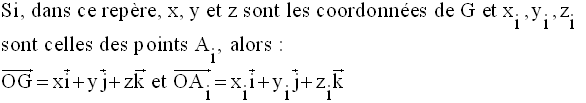
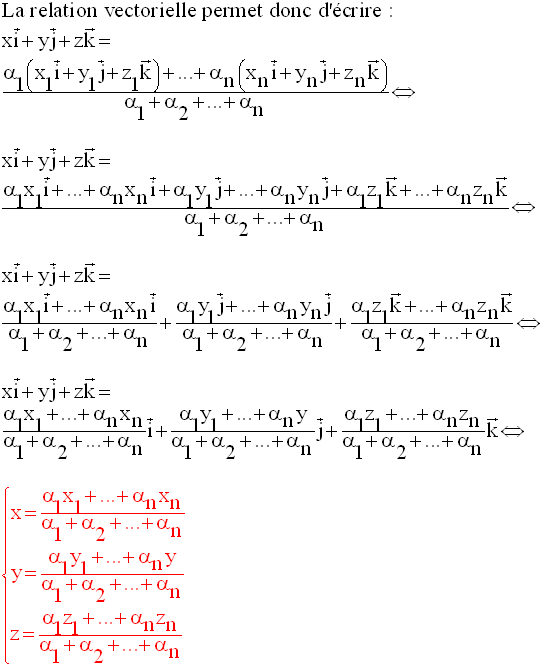
Ce sont là
les relations donnant les coordonnées du barycentre G en
fonction des
coordonnées des points pondérés composant le système.
Exemples
1-


2-

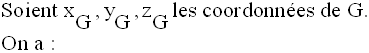
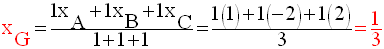
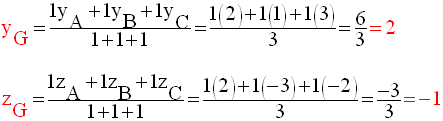
6- Equations cartésiennes
de solides remarquables pris dans un espace muni
d’un repère orthonormal
6-1 La sphère
L’ensemble des points M(x ,
y, z) de cet espace tels que AM est égale à r est
appelée
sphère de centre A et de rayon r.
Cet ensemble sera noté S(A,r).
Le théorème de Pythagore permet d’écrire :
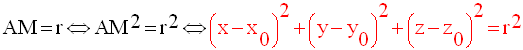
On obtient ainsi l’équation de la sphère de centre A et de rayon r.
Si A
est confondu avec l’origine O du repère,
alors l’équation de la sphère de centre O
et de rayon r s’écrit :
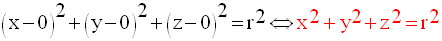
Si r est nul, alors la sphère S(A,0) se réduit à l’ensemble {A}.
Positions relatives d’une sphère et d’un plan
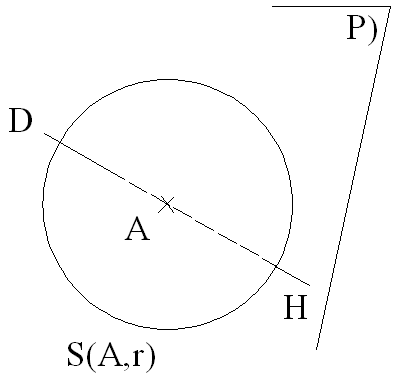
On mène de A la droite D orthogonale au plan P ; elle coupe ce dernier au point H.
Par définition, AH est la distance de la sphère S(A,r) au plan P et on écrit :
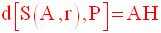
On a les résultats évidents suivants :
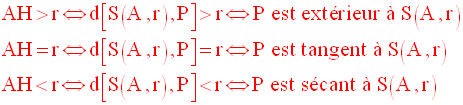
Intersection d’un plan et d’une sphère
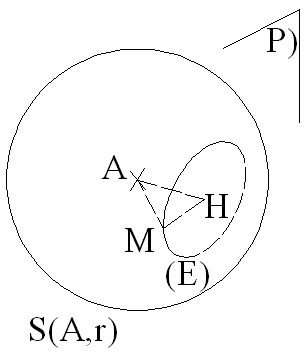
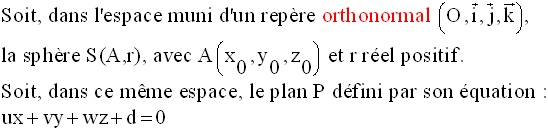
On suppose que P est sécant à S(A,r).
Si la droite passant par A et orthogonale à P coupe ce dernier au point H, alors :
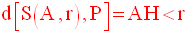
Soit (E) l’intersection de S(A,r) et de P.
(E) est représenté par le système :
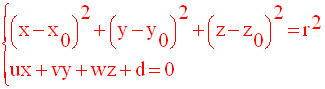
On demande de trouver la nature de (E).
Soit M(x , y , z) un point quelconque de (E).
(AHM) étant un triangle
rectangle en H, on peut lui appliquer le théorème de Pythagore
qui donnera AM :
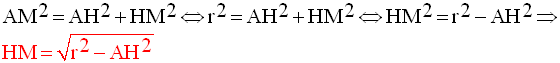
Or A et P étant fixes, la
droite passant par A et orthogonale à P et son intersection
H avec P le sont également.
Par conséquent, la quantité AH est constante.
(E) est donc le cercle de centre H et de rayon égal à :
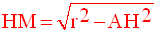
Connaissant r, u, v, w et d, on peut trouver ce rayon.
La méthode
1-
On calcule la distance AH (distance d’un point à un plan). Elle est égale à :
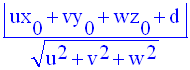
2-
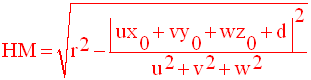
Exemples
1-

Démontre que P est sécant à S(A,4) et calcule le rayon du cercle – intersection.
(L’unité de mesure des longueurs est le centimètre)
Soit D la droite passant par A et orthogonale à P ; elle coupe ce dernier au
point H.

P est donc sécant à S(A,4).
L’intersection est un cercle de centre H et de rayon r’ égal à :
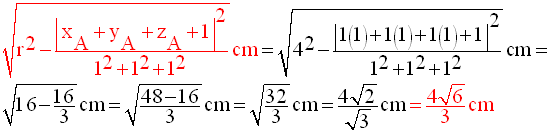
2-

Démontre que Q est sécant à S(O,2) et calcule le rayon du cercle – intersection
(L’unité de mesure des longueurs est le centimètre)
Soit D la droite passant par O et orthogonale à Q ; elle coupe ce dernier au point F.
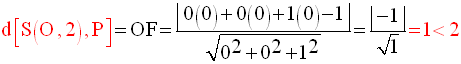
P est donc sécant à S(O,2).
L’intersection est un cercle de centre F et de rayon r’ égal à :

Equation du plan tangent à une sphère en un point de tangence donné
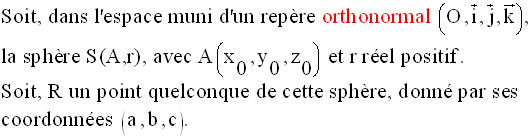
On demande de trouver l’équation du plan P tangent à S(A,r) au point de tangence R.
Soit M(x , y , z) un point quelconque de cet espace.
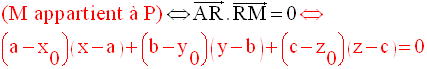
Cette dernière
équation est donc celle du plan P ; en la
développant, on pourra la mettre
sous la forme :
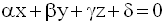
Exemple

On demande de trouver l’équation du plan P tangent à S(O,2) au point de tangence R.
Soit M(x , y , z) un point quelconque de cet espace.
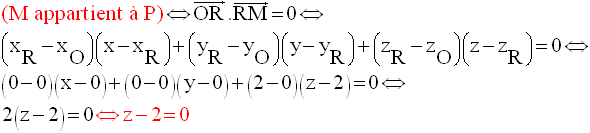
P est le plan parallèle au plan (xOy) du repère et passant par R.
6-2 Le cylindre de révolution
Définition
Soit une direction quelconque D de l’espace muni d’un repère orthonormal R.
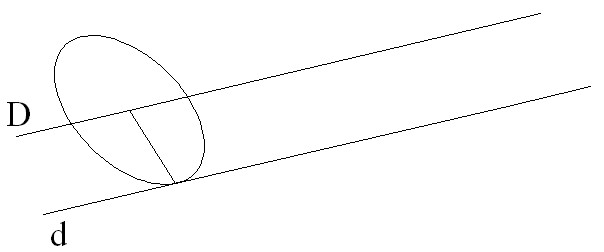
On appelle surface cylindrique de révolution, celle engendrée, par la rotation autour de D, d’une droite d parallèle à D.
d est appelée génératrice de cette surface et D, son axe de révolution.
Soit S cette surface.
Soient dans ce même espace, deux plans P et Q distincts, parallèles et orthogonaux à D.
L’intersection de chacun de
ces plans avec S est un cercle. Les deux cercles,
ainsi
définis, ont leurs centres appartenant à l’axe D
et ont même rayon r.
P et Q délimite ainsi une portion de S appelée cylindre de révolution, droit.
D et d sont respectivement l’axe et la génératrice de ce cylindre.
L’un quelconque des deux
cercles définis précédemment est appelé directrice
ou
base de ce cylindre.
Equations du cylindre de révolution, droit

Soit S cette surface.
L’intersection de S et du plan (xOy) est le cercle (C) de centre A et de rayon r.
L’équation de (C) est donc :
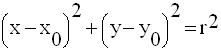
Soient M(x , y , z) un point
quelconque de S et m, sa projection orthogonale dans le
plan (xOy).
Par conséquent m appartient au cercle (C).
On a donc :
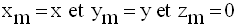
Or, m appartenant à (C), on obtient :
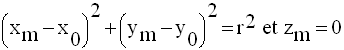
Par conséquent, l’abscisse et l’ordonnée de M vérifient l’équation :
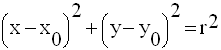
Le système d’équations représentant la surface S est donc :
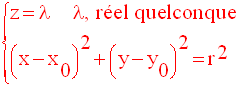
Soit un plan P parallèle à (xOy) et d’équation :

Il coupera S selon un cercle (C’) de même rayon que (C) ; son centre appartient à l’axe D.
La portion de S délimitée
par le plan (xOy) et P est un cylindre de révolution, droit,
d’axe D, de directrice (C) et de génératrice d.
Le système
d’équations représentant ce cylindre est l’un ou l’autre des deux
systèmes
suivants (selon que h est positif ou négatif) :
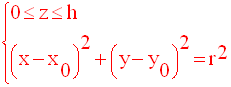
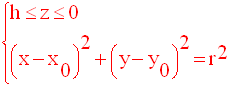
Généralisation
La portion de S
délimitée par deux plans distincts P et Q, parallèles au plan (xOy),
d’équations respectives :
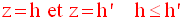
est un cylindre de révolution, droit.
Le système le représentant est :
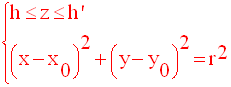
6-3 Le cône de révolution
Définition
Soit une direction quelconque D de l’espace muni d’un repère orthonormal R.
Soit d une droite quelconque sécante à D au point A.
On appelle
surface conique de révolution, celle engendrée,
par la rotation de la droite
d autour de D.
A est appelé sommet de cette surface conique de révolution.
L’angle (D,d) est appelé angle de rotation de cette surface conique de révolution.
d est appelée génératrice de cette surface et D, son axe de révolution.
Soit S cette surface conique de révolution.
Soit dans ce même espace, un plan P tel que :
- A n’appartient pas à P
- D est orthogonale à P
Dans ces conditions, P est
sécant à S et l’intersection est un cercle (C) dont le centre
appartient à D.
La portion de S comprise
entre le sommet A et le plan P est appelée cône de
révolution,
droit d’axe D, de génératrice d.
(C) sera appelé directrice ou base de ce cône.
Equations du cône de révolution, droit
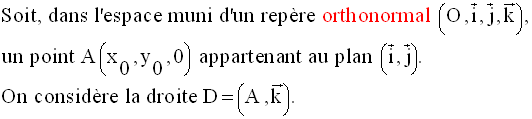

Soit S cette surface.
Soient M(x , y , z) un point
quelconque de S et P le plan passant par M et parallèle
au plan (xOy).
P rencontre D au point H, projeté orthogonal de M sur D.
L’intersection de P et de S est donc un cercle inclus dans P, de centre H et de rayon HM.
M appartenant à ce cercle, on obtient le système :
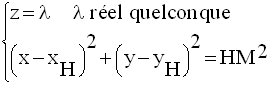
Or,
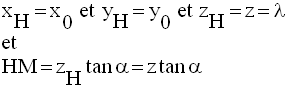
Le système s’écrit alors :
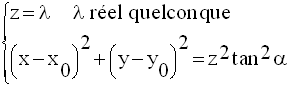
En posant tan α égale à a, on obtient finalement :
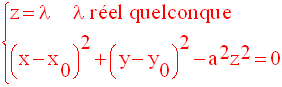
C’est le système d’équations représentant la surface conique de révolution, droite S.
Soit un plan Q parallèle à (xOy) et d’équation :
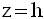
La portion de S délimitée
par le sommet A et Q est un cône de révolution, droit,
de sommet A, d’axe D, de directrice le cercle intersection de S et de P (C) et
de
génératrice d.
Le système
d’équations représentant ce cône est l’un ou l’autre des deux systèmes
suivants (selon que h est positif ou négatif) :
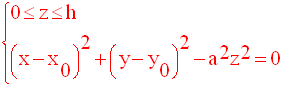
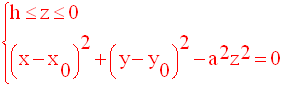
Généralisation
La portion de S
délimitée par deux plans distincts Q et R, parallèles au plan (xOy),
d’équations respectives :
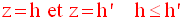
est représentée par le système d’équations :
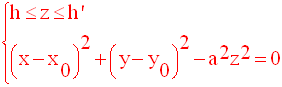


suites numériques
(groupes ciblés : premières toutes séries
confondues)
Étudie la monotonie des suites numériques suivantes :
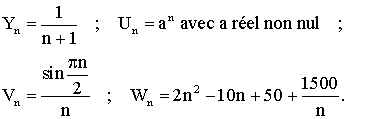
La suite numérique suivante :
![]()
est-elle convergente ?
Étudie la convergence de la suite numérique :
![]()
un peu de trigonométrie
(groupes ciblés : premières scientifique et
technologique)
1- Exprime en fonction de sin x ou de cos x les
expressions
suivantes :
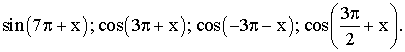
2- Exprime en fonction de tg x ou de cotg x les
expressions
suivantes :
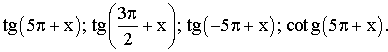
3- Simplifie :
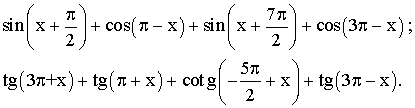
4- Démontre les identités suivantes :
cos4 x - sin4 x + 2 sin2 x = 1 ;
cos4 x - sin4 x - 1 = - 2 sin2 x cos2
x ;
cos6 x + sin6 x - 1 = - 3 sin2 x cos2
x ;
2 cos6 x + 2 sin6 x + 1 = 3 (sin4 x + cos4
x) ;
(tg x + cotg x) sin x cos x = 1 ;
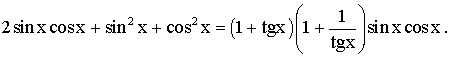
5- Démontre l'énoncé :
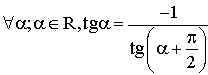
En déduire la relation qui doit lier les pentes de deux droites rectangulaires dans un repère orthonormé .
Que peut-on dire des droites dont les pentes sont
racines
de l'équation :
x2 - (m + 1) x - 1 = 0 ?
6- t étant la variable réelle, trouve la
période de la fonction x suivante :
x = sin t - 3 cos 2t .
Je te rappelle que la fonction x = f(t) est dite périodique de période T,
lorsque : f(t + T) = f(t) , pour tout t , élément du domaine de
définition de f .
puissance d'un point par rapport à un cercle
et
axes radicaux de deux cercles
(groupe ciblé : première S)
Rappel
Dans un plan, la puissance d'un point M par
rapport à un cercle (C)
![]()
Soit (MT) la tangente issue de M à (C) , T
étant le point de tangence . Soit une droite sécante quelconque (d) passant
par M et coupant (C) en P et Q .
![]()
Soient, dans un plan, deux cercles quelconques
(C) et (C') .
On appelle axe radical de (C) et (C') l'ensemble des points M de leur
plan ayant même puissance par rapport à ces deux cercles .
Démontre le théorème suivant :
Dans un trapèze, l'intersection des diagonales appartient à l'axe radical
des deux cercles construits sur ses côtés non parallèles .
C'est le théorème de Richa .
Soit maintenant dans un plan, un trapèze
quelconque (ABCD) de côtés parallèles [AB] et [DC] .
On pose AB = a ; DC = b
; AD = d et BC = d' .
Soit M le milieu de la base moyenne .
I étant l'intersection des diagonales, O, O' étant respectivement les milieux
de [AD] et [BC], H étant la projection orthogonale de I sur la base moyenne.
Quelle relation doivent vérifier a, b, d et d' pour que
MH soit égale au quart de OO' ?
une transformation trigonométrique
(groupes ciblés : premières toutes séries confondues)
A tout point M de coordonnées x et y d'un plan rapporté à un repère orthonormé, on associe l'équation :
a cos 2t+x sint+y = 0 (1)
où a est un réel donné et
t la mesure d'un angle inconnu exprimé en radians .
![]()
1- Détermine l'ensemble des points M du plan
pour lesquels l'équation (1) admet une racine double (c'est-à-dire deux
racines égales) ; pour cela tu pourras former l'équation ayant pour inconnue X
= sint .
2- Précise les régions du plan pour lesquelles (1) admet deux racines .