(groupes ciblés : terminales , toutes séries confondues)
les thèmes abordés dans cette page
étude du signe
du trinôme du second degré
(première S)
intégrale et limite d'une suite
(terminale S)
axe
radical
(première et terminale S)
congruences (modulo n) dans Z
(terminale S)
encadrement d'une racine d'une équation -
logarithme
(terminale L)
analyse combinatoire
(terminales)
dérivation et extremums d'une fonction
numérique
(terminales)
extremums
d'une fonction numérique et géométrie
(terminales S et technologiques)
étude d'une fonction numérique et
dérivation
(terminale L)
homothétie et somme
(terminale S)
un peu de cinématique
(terminales S et technologiques)
de la métrique dans
un triangle
(terminale S)
étude du signe du trinôme du second degré
(groupe ciblé : première S)
1- Définitions
Un trinôme à une variable réelle est un polynôme composé de trois termes appelés monômes.
Exemples :
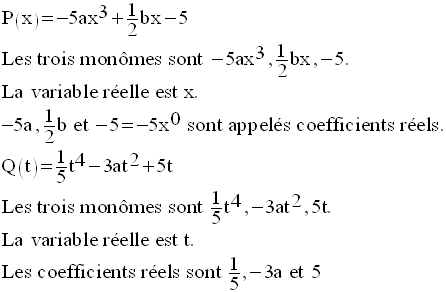
On appelle degré d’un trinôme à une variable réelle le plus grand exposant affecté à cette variable et se trouvant dans au moins un des trois monômes.
Exemples :
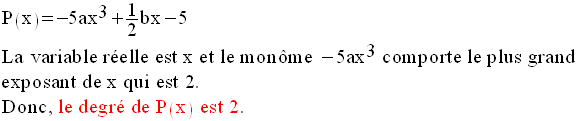
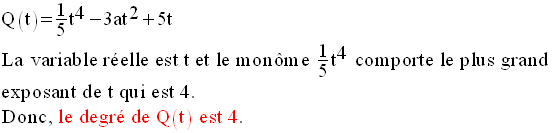
Si le degré d’un trinôme à une
variable est n, on dira alors qu’il est du nième
degré par rapport à
cette variable.
Dans les exemples ci-dessus, P(x)
est du second degré par rapport à x et Q(t) est du quatrième
degré par rapport à t.
Un
trinôme à une variable réelle et du second degré par rapport à cette variable
est de
la forme générale :
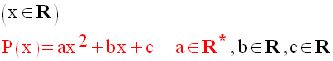
Exemples :

Remarque importante
Le coefficient a du monôme de degré 2 par rapport à la variable est un réel différent de zéro.
Cette condition est importante
puisqu’avec a nul, le trinôme se réduit à un binôme, au plus
du premier degré par rapport à la variable.
2- Etude du signe d’un trinôme à une variable et du second degré par rapport à cette variable
Lorsque la variable parcourt R, ce trinôme est partout défini dans R et, à son tour, va parcourir R.
Le but de notre étude est de déterminer quelles sont les parties de R dans les quelles ce trinôme est nul, strictement négatif ou strictement positif, ou encore de déterminer les conditions que doivent remplir certains coefficients de ce trinôme pour qu’il soit nul ou strictement négatif ou strictement positif.
C’est ce qu’on appelle souvent « étude
du signe du trinôme à une variable réelle, du second degré
par rapport à cette variable ».
Pour cela, on commencera à écrire ce trinôme sous une forme qui permet de rendre plus facile cette étude.
Soit la forme générale :
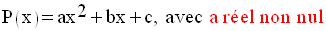
a étant différent de 0, il peut être mis en facteur ; on obtient :
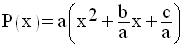
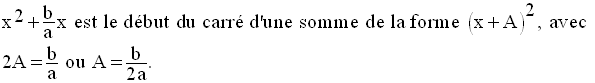
Ainsi, on a :
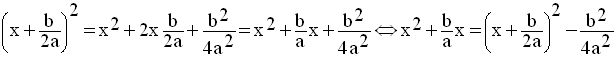
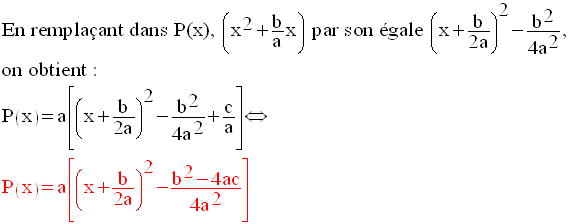
C’est cette dernière forme qui va être utilisée dans l’étude.
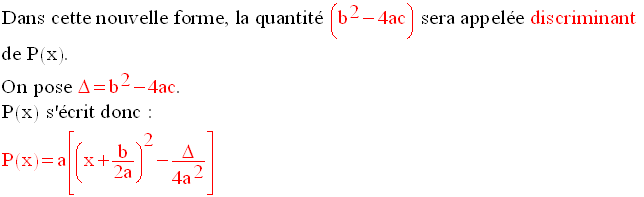
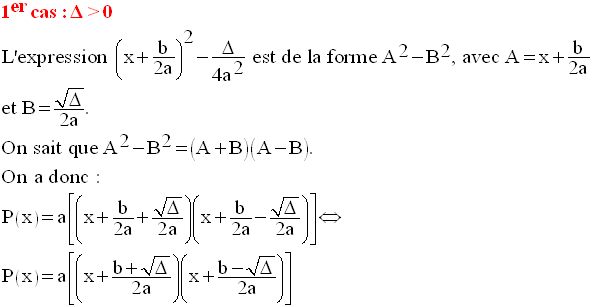
Pour qu’un produit de facteurs soit nul, il faut et il suffit qu’au moins un de ces facteurs le soit.
Ainsi, a étant non nul, P(x) s’annule si et seulement si :
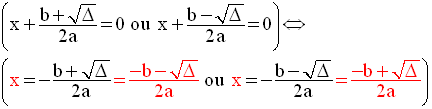
Première conclusion
Si le discriminant
est strictement positif, alors P(x) s’annule pour deux valeurs
distinctes de
la variable, souvent appelées les racines ou solutions de
l’équation P(x) = 0 ou encore les
zéros de P(x).
Ces zéros réels sont :
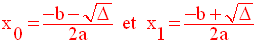
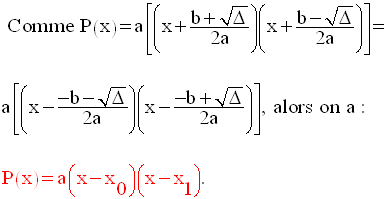
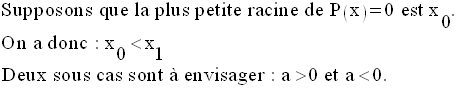

Conclusion générale
Si le discriminant
est strictement positif, alors P(x) admet deux zéros réels
distincts.
De plus, P(x) est de même signe que son coefficient a pour les valeurs de la
variable
extérieures à ses zéros, de signe contraire à celui de son coefficient a pour
les valeurs de
la variable strictement comprises entre ses zéros.
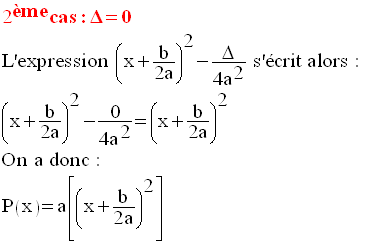
Ainsi, a étant non nul, P(x) s’annule si et seulement si :
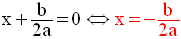
Première conclusion
Si le discriminant
est nul, alors P(x) s’annule pour une valeur et une seule de la variable,
souvent
appelée racine double de l’équation P(x) = 0.
On dit aussi que P(x) admet un et un seul zéro réel.
Ce zéro est :
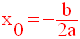
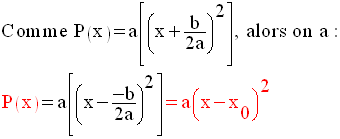
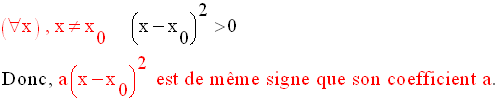
Conclusion générale
Si le discriminant
est nul, alors P(x) admet un et un seul zéro réel.
De plus, P(x) est de même signe que son coefficient a pour les valeurs de la
variable
différentes de son zéro.
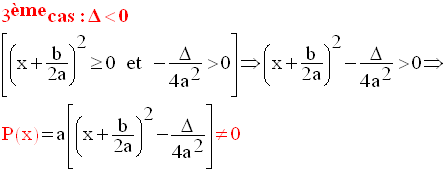
Première conclusion
Si le discriminant
est strictement négatif, alors P(x) ne s’annule pour aucune valeur de
la variable.
L’équation P(x) = 0 n’admet aucune racine réelle.
On dit aussi que P(x) n’admet aucun zéro réel.
Par ailleurs, on a :

Conclusion générale
Si le discriminant
est strictement négatif, alors P(x) n’admet aucun zéro réel.
De plus, P(x) est de même signe que son coefficient a pour toute valeur
réelle de la variable.
3-
Deux propriétés importantes portant sur les
conditions d’existence des zéros d’un
trinôme à une variable et du second degré par rapport à cette variable
Soit P(x) un trinôme à une variable et du second degré par rapport à cette variable.
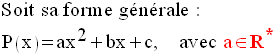
On a vu que P(x) s’écrit également :
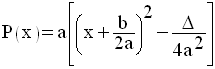
Propriété 1
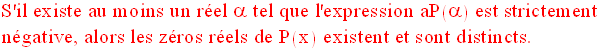
Démonstration
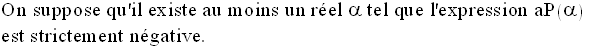
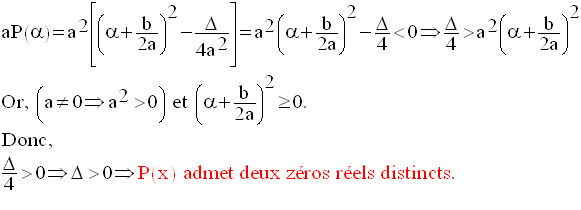
La réciproque est vraie.
En effet,
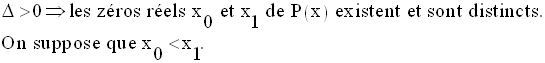

Conclusion

Propriété 2
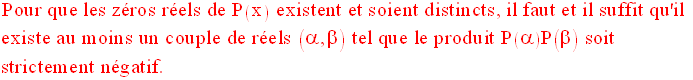
Démonstration
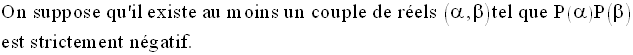

Ainsi, d’après la propriété 1, les zéros réels de P(x) existent et sont distincts.
Réciproquement, on a :
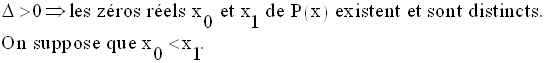

4- Somme et produit des zéros
On a vu que si le discriminant
est strictement positif, alors P(x) s’annule pour deux valeurs
distinctes de la variable, souvent appelées les racines ou solutions
de l’équation P(x) = 0 ou
encore les zéros réels de P(x).
De plus, P(x) peut se mettre sous la forme :
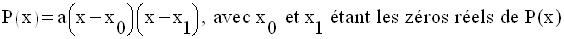
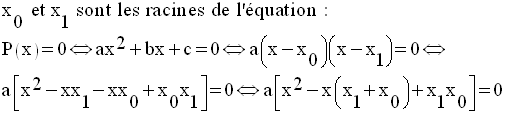

5- Applications
Application 1
On donne le trinôme suivant :
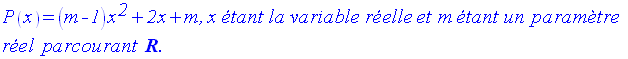
On te demande de
trouver l’ensemble des valeurs de m pour que P(x) admette deux
zéros réels et distincts.
Solution
On a :
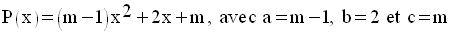
D’abord, P(x) devant être un trinôme du second degré en x, son coefficient a = m – 1 doit être strictement positif, donc :
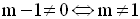

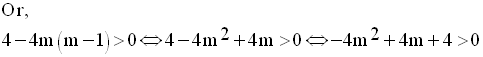
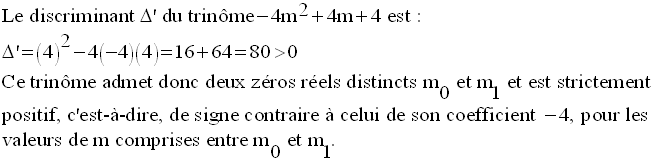
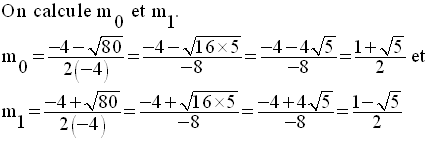
Ainsi,
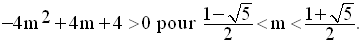
Comme m devra être également
différent de 1, l’ensemble des
valeurs de m pour que
P(x) admette deux zéros réels et distincts est :
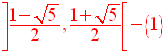
Application 2
On donne un
polynôme P(x), de degré n (n entier naturel largement supérieur à 2),
par rapport à la variable x, sous sa forme générale :
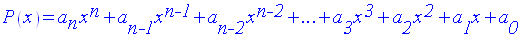
La division euclidienne de P(x) par (x – a) permet d’écrire :
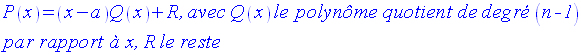
1-
Démontre que le reste est égal à P(a).
2-
Démontre que P(x)
admet a pour zéro si et seulement si P(x) est divisible par
(x – a).
3-
Quelle relation devront vérifier les coefficients de P(x) pour que 1 soit zéro de P(x) ?
4-
Quelle relation devront vérifier les coefficients de P(x) pour que – 1 soit zéro de P(x) ?
5-
Application
On te demande de résoudre dans R l’inéquation :
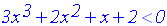
Solution
1-
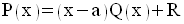
En remplaçant dans cette égalité x par a, on obtient :

Donc,
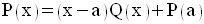
2-

Ce qui implique que P(x) est divisible par (x – a).
Réciproquement, supposons que P(x) est divisible par (x – a).
Le reste, P(a), da la division de P(x) par (x – a) est donc nul.
3-
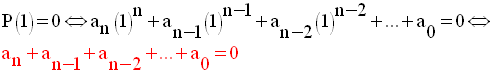
1 est un zéro de P(x) si seulement si la somme de ses coefficients est nulle.
4-
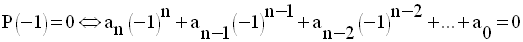
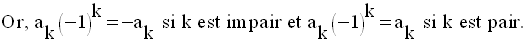
(– 1) est zéro de
P(x) si seulement si la somme des coefficients des monômes de degrés
pairs est égale à la somme des coefficients des monômes de degrés impairs.
5-
Application
Soit à résoudre dans R, l’inéquation :
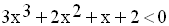
On pose et on a :
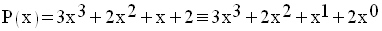
La somme des coefficients des
monômes de degrés pairs est 2 + 2 = 4 et celle
des
coefficients des monômes de degrés impairs est 3 + 1 = 4.
Ces deux sommes étant égales, P(– 1) est nul ; donc P(x) est divisible par :
[x – (– 1)] = (x + 1).
P(x) est donc de la forme :
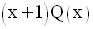
Avec Q(x) de degré par rapport à x égal à 3 – 1 = 2.
Q(x) est donc un trinôme de second degré par rapport à x.
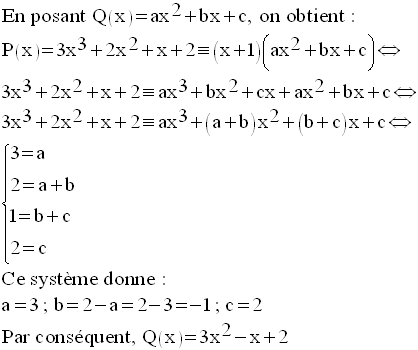
L’inéquation donnée s’écrit donc :
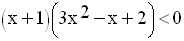
Le discriminant de Q(x) est égal à :
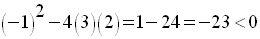
Donc Q(x) est de même signe que celui de son coefficient a = 3 pour tout réel x.
Ainsi,
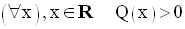
Par conséquent,
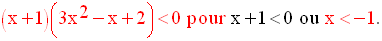
Application 3
On donne un trinôme P(x) du second degré par rapport à x.
Sa forme générale est :
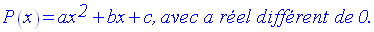
On suppose que son discriminant est largement positif.
Trouve, en fonction de ses coefficients, la somme e le produit de ses zéros.
Application :

Solution
Puisque le discriminant de P(x) est largement positif, les zéros de P(x) existent.
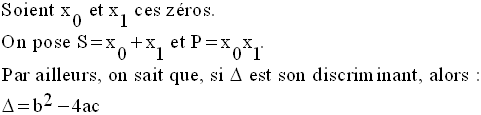
On a :
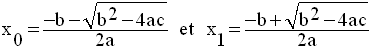
Ce qui donne :
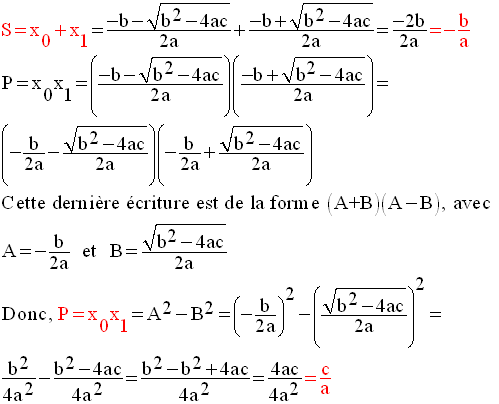
Application
On a :
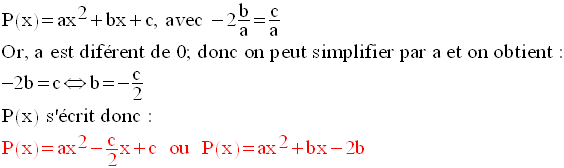
Application 4
On donne un trinôme P(x) du second degré par rapport à x :
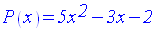
Démontre, sans calculer son discriminant, que P(x) admet deux zéros réels et distincts.
Solution
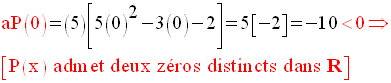
Application 5
On donne un trinôme P(x) du second degré par rapport à x :
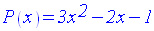

Solution
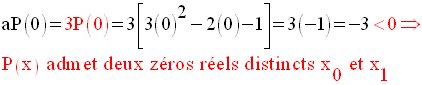
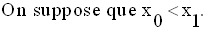
On a :
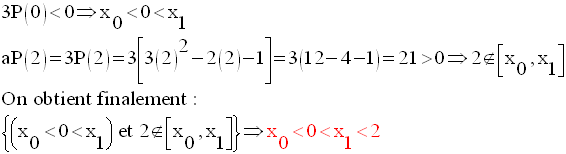
Application 6
On donne un trinôme Q(x) du second degré par rapport à x :
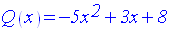
1-
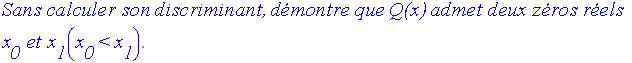
2-
Comment 2 et 3 se positionnent-ils par rapport à ces zéros ?
Solution
1-

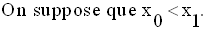
2-

Par conséquent,

Application 7
On donne un trinôme R(x) du second degré par rapport à x :
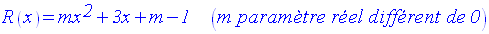
1-
Etudie en fonction des valeurs de m l’existence des zéros de R(x).
2-
Etudie en
fonction des valeurs de m la position des réels 1 et 2 par rapport aux zéros,
quand ils existent, de R(x).
Solution
1-
Pour étudier l’existence des zéros de R(x), on doit étudier le signe de son discriminant.
On a :

2-
On suppose que les zéros de R(x) existent et sont :
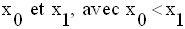
La condition que vérifie m est donc :
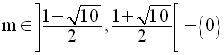
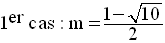
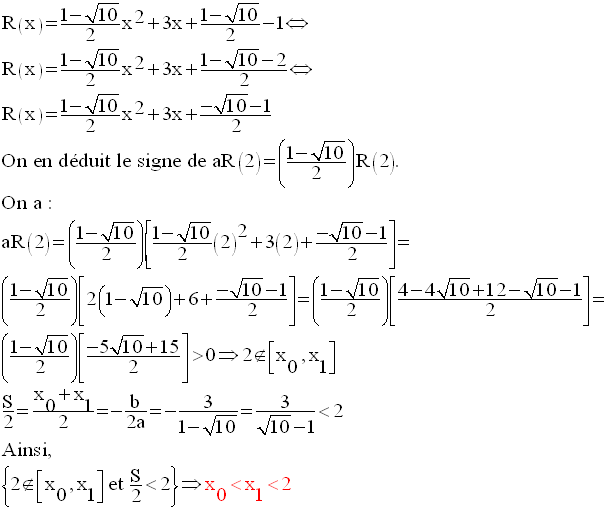

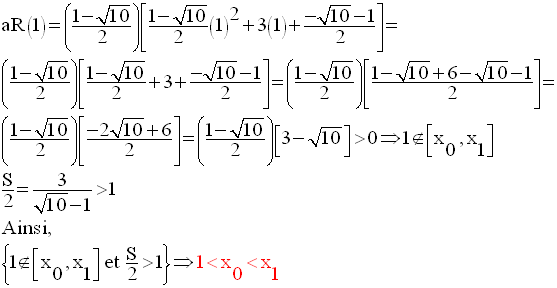
Finalement,
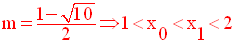
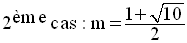
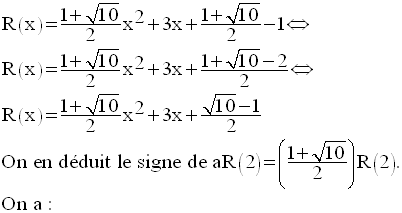
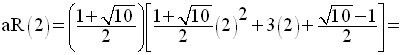
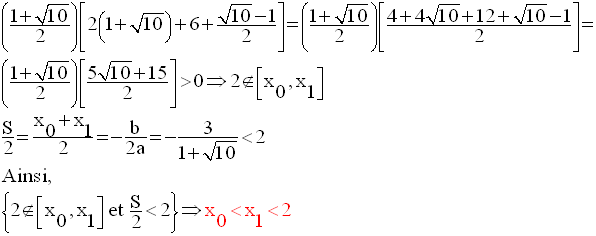
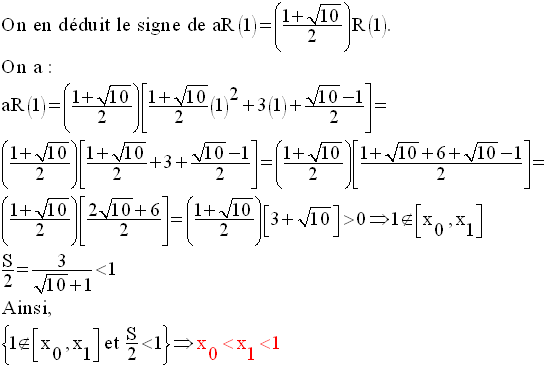
Finalement,
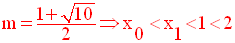
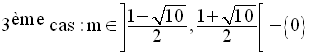
Dans ce cas, R(x) s’écrit :
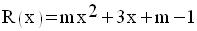
On doit étudier les signes des expressions :
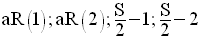
en fonction du paramètre m.
On exprime d’abord, chacune de ces quantités en fonction de m.
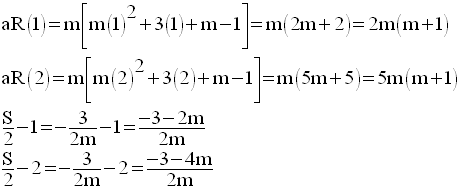
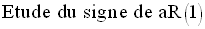
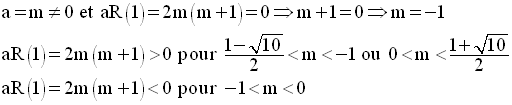
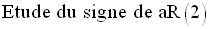
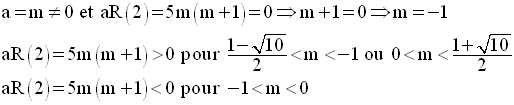
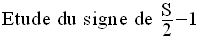
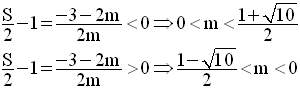
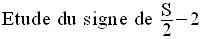
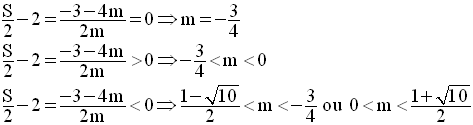
Il reste à étudier les cas suivants :
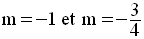
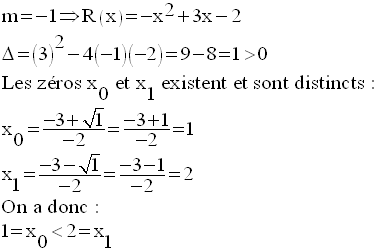
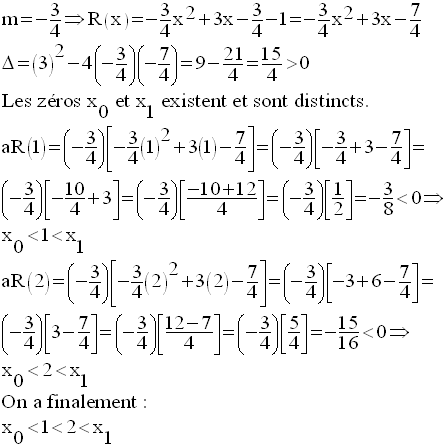
On rassemble ensuite toutes ces données et leurs conclusions dans un tableau,
comme suit :

Comment renseigne-t-on ce tableau ?
Les deux lignes d’extrémités sont hachurées pour indiquer que les valeurs de m au-delà de :
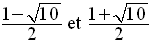
sont exclues.
La première ligne correspond à l’intervalle :
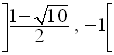
Dans cet intervalle, on lit :
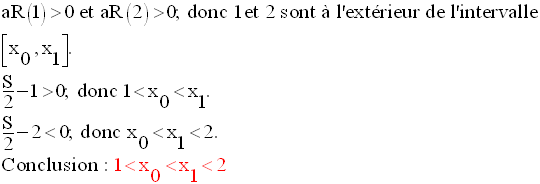

La seconde ligne correspond à l’intervalle :
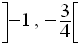
Dans cet intervalle, on lit :
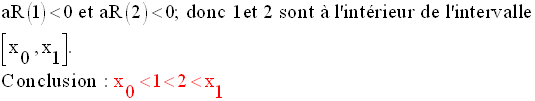
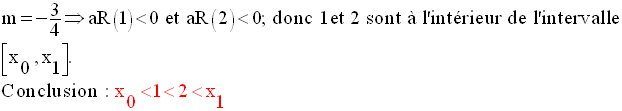
La troisième ligne correspond à l’intervalle :
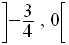
Dans cet intervalle, on lit :
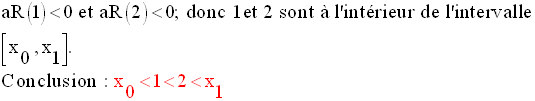
Le trait correspondant à m = 0 a
été doublé pour indiquer l’exclusion de cette valeur
de m qui réduit l’équation en une équation du premier degré en x.
La quatrième et dernière ligne correspond à l’intervalle :

Dans cet intervalle, on lit :
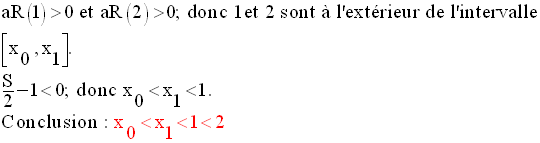
On pourra ajouter dans ce
tableau, au niveau des deux traits correspondants
aux deux valeurs de m :
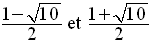
les résultats obtenus tout au début :
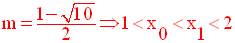
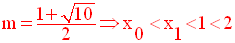
Application 8
On donne l’équation en x :
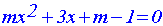
Etudie, en fonction du paramètre réel m, l’existence et le signe des racines de cette équation.
Solution
Pour ce type d’exercice, la méthode à suivre est la suivante :
1-
On étudie le ou les cas où l’équation se réduit à une équation du premier degré par rapport à son inconnue.
2-
Les valeurs du paramètre pour
lesquelles l’équation se réduit à une équation du premier degré
par rapport à l’inconnue écartées, on exprime en fonction du paramètre, le
discriminant de
l’équation et on étudie son signe.
On aura ainsi répondu à la première partie de la question, à savoir l’existence des racines.
3-
Dans l’ensemble des valeurs du
paramètre où les racines existent, on exprime les
quantités suivantes,
en fonction du paramètre, et on étudie leurs signes :
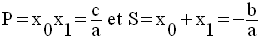
4-
On rassemble tous les résultats dans un tableau.
Application de cette méthode à notre exercice
Pour m nul, l’équation se réduit à l’équation du premier degré en x :
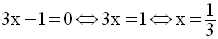
On suppose pour la suite que m est différent de 0.
On exprime, en fonction de m, le discriminant de l’équation :
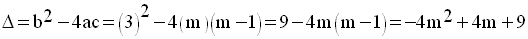
On étudie le signe de ce discriminant en fonction de m.
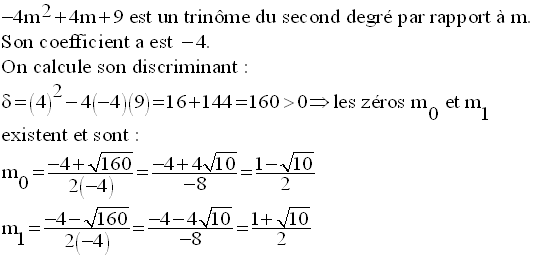
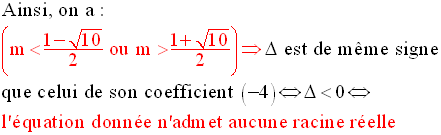
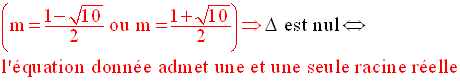

Dans l’ensemble des valeurs de m :
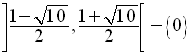
on étudie les signes respectifs des quantités S et P, S étant la somme des racines et P, leur produit.

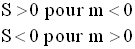

On rassemble ensuite toutes ces données et leurs conclusions dans un tableau.
A titre d’exercice, je te laisse renseigner ce tableau en tirant les conclusions.
Pour cela, il faut savoir que :
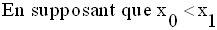
Dans tout intervalle portant sur
m où P est strictement positif, les deux racines sont de même
signe ; si de plus, S est strictement positive, alors :
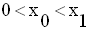
Dans tout intervalle portant sur
m où P est strictement positif, les deux racines sont de même
signe ; si de plus, S est strictement négative, alors :
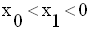
Dans tout intervalle portant sur
m où P est strictement négatif, les deux racines sont de
signes contraires ; si de plus, S est strictement positive, alors :
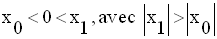
Dans tout intervalle portant sur
m où P est strictement négatif, les deux racines sont de
signes contraires ; si de plus, S est strictement négative, alors :
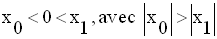
Dans tout intervalle portant sur m où P est nul, une des racines est nulle et l’autre sera égale à :
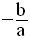
Dans tout intervalle portant sur
m où P est strictement négatif, les deux racines sont de
signes contraires ; si de plus, S est nulle, alors les deux racines sont
opposées :
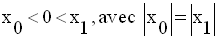
Application 9
Résous dans R les inéquations suivantes :
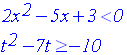
Solution
Le but de cet exercice est de te
montrer que l’on a plus, comme on faisait en troisième ou
en seconde, à factoriser et à établir un tableau pour trouver les solutions
d’une inéquation
du second degré par rapport à sa variable.
On devra
utiliser les résultats de l’étude du signe du trinôme du second degré par
rapport à sa variable.

On veut que ce trinôme soit
strictement négatif, c’est-à-dire de signe contraire à celui de
son coefficient a.
Donc, on a :
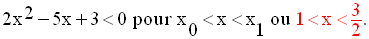
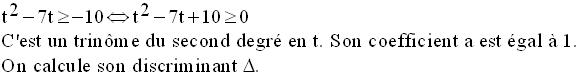
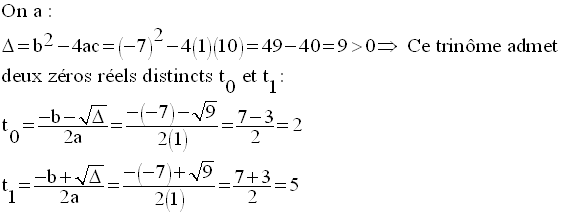
On veut que ce trinôme soit
largement positif, c’est-à-dire de même signe que celui de son
coefficient a ou nul.
Donc, on a :
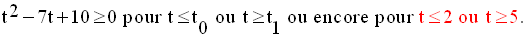
Application 10
Deux réels ont leur somme égale à 17 et leur produit égal à 60.
Calcule ces deux réels.
Solution
Soient a et b ces deux réels.
Par hypothèse, on a :
a + b = S = 17 et ab = P = 60
Ces deux réels sont donc les racines de l’équation :

Pour trouver a et b, il suffit donc de résoudre cette équation.
Son discriminant est :
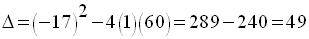
On obtient finalement :
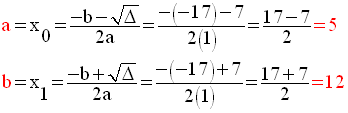
Application 11
On donne l’équation :
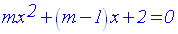
Pour quelles valeurs du paramètre réel m ses racines existent-elles ?

Solution
On calcule le discriminant de cette équation :
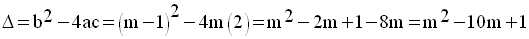
On étudie ensuite le signe de ce discriminant en fonction du paramètre m.

D’où le résultat :

Dans toute la suite, on suppose que les racines existent.
Donc :
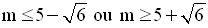
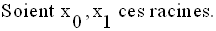
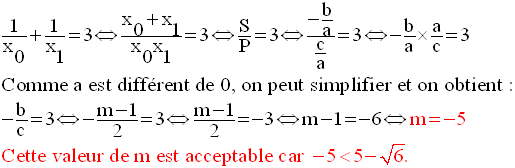
Application 12
Première partie
On donne sur un axe orienté quatre points A, B, C et D d’abscisses respectives a, b, c et d.
On dira que A, B, C et D forment une division harmonique si et seulement si :
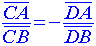
On dira que A et B sont harmoniques par rapport à C et D.
Quelle est dans ce cas la relation que doivent vérifier les abscisses de ces quatre points ?
Deuxième partie


Solution
Première partie

Deuxième partie
1-
L’équation de l’axe des abscisses (x’x) est y = 0.
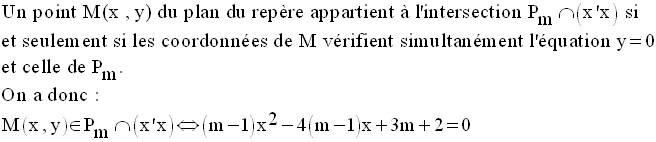
Etudier le nombre d’intersection
de la parabole donnée avec l’axe des abscisses revient
donc à étudier l’existence des racines de l’équation aux abscisses :
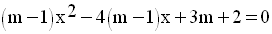
On calcule donc le discriminant de cette équation.
On a :
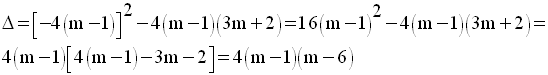
D’où les résultats :
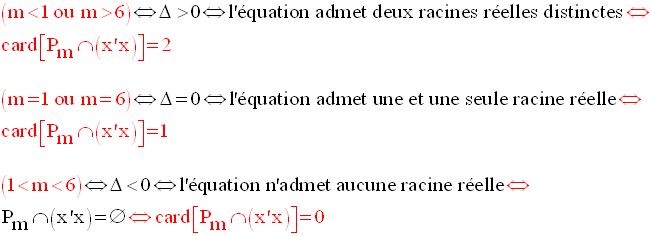
2-
On a :
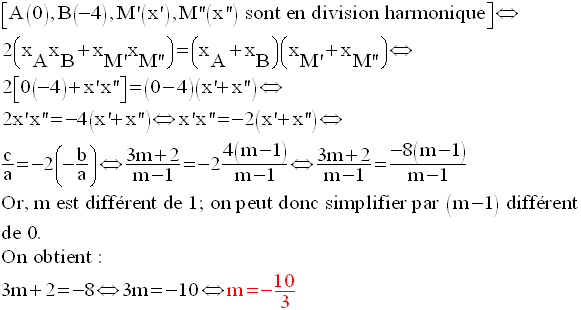
intégrale et limite d'une suite
(groupe ciblé : terminale S)
Soit f une fonction réelle d'une variable réelle intégrable sur [a , b] .
Tu vas admettre l'égalité importante suivante :
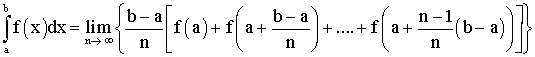
Trouve la limite , lorsque n tend vers l'infini (n étant un entier naturel quelconque différent de 0) , de la suite définie par :
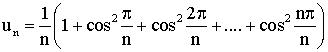
Trouve la limite , lorsque n tend vers l'infini
(n étant un entier naturel quelconque différent de 0) , de la suite définie par :
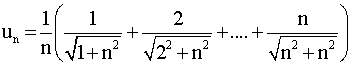
D'abord je te rappelle qu'une suite réelle est
une application d'une partie I de N dans R (généralement I est
égale à N ou N*) .
Ainsi , si tu notes A cette application , pour
tout n élément de I , l'image de n par A , notée A(n) , peut être également
notée : un ,
avec un réel .
L'expression A(n) définissant la suite peut être donnée en fonction
de n ou
en fonction de termes précédents A(n-1) ; A(n-2) ; etc.
La suite correspondante sera notée :
![]()
Ensuite essaie d'interpréter géométriquement
l'égalité importante donnée au début des travaux précités .
Tu
t'apercevras qu'elle n'est pas aussi difficile que tu le croyais .
Pour trouver les limites demandées des suites
données ci - dessus , évidemment il faudra que tu appliques cette égalité fondamentale
.
Pour cela , il te faudra trouver
d'abord qu'elle est la fonction intégrable sur un certain intervalle à
déterminer également ; ceci bien sûr à partir de l'expression donnée de
chacune de ces suites .
Pour t'aider la fonction intégrable est f(x) = cos2 x , pour la première suite ; celle tirée de la seconde suite est :

A toi de jouer maintenant .
un théorème
(groupes ciblés : terminales toutes séries scientifiques
confondues)
Rappel
Dans un plan, soit un cercle (C) de centre O et
de rayon r .
Soit un point M quelconque .
On appelle puissance de M par rapport au cercle (C) et on la note P(C)
(M), l'expression :
d2 - r2 .
Dans un plan, on appelle axe radical de
deux cercles quelconques (C); (C'), l'ensemble des points M ayant même
puissance par rapport à ces deux cercles; c'est-à-dire :
P(C) (M) = P(C')
(M) .
Tu peux facilement montrer que cet ensemble est bien une droite perpendiculaire
à la ligne des centres de (C) et (C') .
Tu vas maintenant démontrer le théorème
suivant :
L'intersection des diagonales d'un trapèze appartient à l'axe radical des
deux cercles construits sur les côtés non parallèles .
C'est le théorème de Richa .
Soit le trapèze (ABCD) dont les côtés
parallèles sont [AB] et [CD] .
On pose AB = a ; CD = b .
O et O' sont respectivement les milieux de [AD] et [BC] ; on pose 2r = AD
et 2r' = BC ; on suppose r' strictement supérieure à r .
Soient I l'intersection des diagonales, M le milieu de la base
moyenne [OO'] .
On définit l'axe (OO') de la manière suivante :
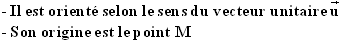
Trouve l'abscisse xi de la projection orthogonale i de I sur (OO') .
xi nulle,
est-elle une condition nécessaire et suffisante pour que le trapèze (ABCD) soit
un trapèze isocèle ?
Sachant que
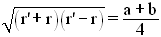
quelle est alors la position de i sur (OO') ?
congruences (modulo n) dans Z
(groupe ciblé : terminale S)
Construis les tables d'addition et de multiplication sur Z/5 .
Résous dans Z/5 les équations suivantes :
![]()
a et b désignant des éléments de
Z/5 ,
discuter dans Z/5 les deux équations :
![]()
Dans cet exercice tu utiliseras les propriétés du groupe additif (Z ; +) et du groupe multiplicatif (Z* ; .) .
Rappel : dans un ensemble A muni d'une loi de
composition
interne o , on dira que A possède la structure de groupe pour
cette
loi si et seulement si :
- pour tous x , y , z éléments de A , (xoy)oz =
xo(yoz) ;
on dira que la loi o est associative dans A ;
- il existe un élément e de A tel que pour tout x de A
xoe = eox = x ; on appellera
e élément neutre pour la loi o ;
- pour tout élément x de A , il existe un élément x' de A tel que
xox' = x'ox
= e ; on appellera x' élément symétrique de x
pour la loi o .
Si de plus , la loi de composition interne o est
commutative ; c'est-à-dire si pour tous x ; y de A , xoy = yox , on dira que
le
groupe est commutatif ou abélien .
le groupe A muni de la loi de composition interne o sera noté (A ; o) .
encadrement d'une racine d'une équation -
logarithme
(groupe ciblé : terminale L)
On donne la fonction réelle d'une variable
réelle x définie
par :
![]()
1- Quel est le domaine de définition D de f ?
2- Étudie f sur son domaine et trace sa courbe représentative
![]()
3- Au regard de ce qui a été dit aux questions 1 et 2 , montre que l'équation
:
x + Log x = 0 admet dans D une racine et une seule x0 telle que :
0,5 < x0 < 0,75 .
Tu utiliseras la continuité de f , sa monotonie , ainsi que son changement
de signe dans l'intervalle
[0,5 ; 0,75] .
4- Trouve l'équation de la tangente T à C au point de cette dernière
d'abscisse x = e .
5- calcule l'aire de la surface A comprise entre les courbes
x = 0 ; y = 0 ; C
et T .
analyse combinatoire
(groupes ciblés : terminales toutes séries
confondues)
Rappel
Prends un ensemble E de n éléments , n étant
un entier naturel différent de 0 .
On appelle arrangement de ces n éléments p à p (p étant un entier
naturel différent de 0 et largement inférieur à n) , tout assemblage de p de
ces éléments dans un ordre de succession déterminé, noté :
![]()
Il y a n.(n -1).(n - 2).(n - 3).....[(n - (p-1)] arrangements; et cette quantité est notée :
![]()
Ainsi on obtient :
![]()
Exemple : combien peux-tu former de nombres de deux chiffres distincts ?
L'ensemble des chiffres est A = {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}. Je te laisse continuer .
Attention : au nombre d'arrangements trouvé, il faudra soustraire celui des arrangements de la forme 0X , avec X appartenant à A*.
Si p est égal à n, alors les arrangements tels que :
![]()
sont appelés permutations des n éléments
et on désigne leur quantité par Pn .
Ainsi
![]()
Pn se note aussi n! qui se lit
"factorielle n".
Par convention on notera 0! = 1 et ainsi l'expression x! est définie sur N .
Exemple : combien de nombres de dix chiffres distincts peux-tu former avec les dix premiers entiers naturels . Là également, il te faudra soustraire de ce nombre, celui des éléments tels que 0ABCDEFGHI .
Reprends l'expression :
![]()
Multiplie le numérateur et le dénominateur (
égal à 1) de cette expression par :
(n - p).(n - p - 1).(n - p - 2).....3.2.1 et en déduis que :
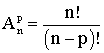
On appelle "combinaison" de p
éléments pris dans un ensemble de n éléments ( n largement supérieur
à p), tout ensemble que l'on peut former en choisissant p de ces
éléments, l'ordre étant cette fois-ci indifférent .
On la note :
![]()
Deux combinaisons ne diffèrent que si l'un au
moins des éléments figurant dans l'une d'elles n'est pas contenu dans l'autre
.
Il y a donc moins de combinaisons que d'arrangements .
Le nombre des combinaisons, noté :
![]()
est égal à :
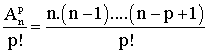
Prends l'expression située au numérateur de la fraction
ci-dessus :
n.(n - 1)....(n - p + 1) .
En multipliant les termes de la fraction :
n.(n - 1)....(n - p + 1) / 1 par (n - p)...1, tu obtiendras l'expression :
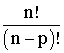
En revenant à l'égalité :
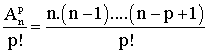
et en remplaçant n.(n - 1)....(n - p + 1) par son égale
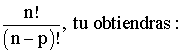
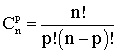
Exemple :
Combien de segments peux-tu former avec 9 points d'un plan , deux à deux
distincts ?
Démontre les deux formules utiles suivantes:
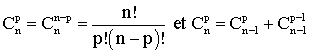
Tu vas , dans la suite , établir le binôme de Newton :
Soit à effectuer le produit suivant :
P = (x + a)n = (x + a).(x + a).(x + a)......(x + a) , n fois .
Un terme s'obtient en choisissant x dans p facteurs (p étant largement inférieur à n) et a dans les (n - p) autres facteurs . Un tel terme est an - p xp .
Il y a autant de tels termes que de choix possibles de p facteurs parmi les n facteurs , sans tenir compte de l'ordre ; quel est alors le nombre de termes de la forme : an - p xp ?
Ainsi , tu obtiens :
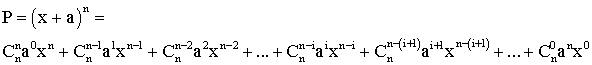
Calcule
![]()
Tu trouveras que ces deux quantités sont égales à 1
D'où
![]()
Comme
![]()
tu obtiens :
![]()
C'est finalement le binôme de Newton .
Il peut s'écrire :
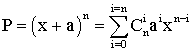
Les quantités telles que :
![]()
sont appelées coefficients du binôme de Newton .
Tu peux facilement démontrer le théorème
suivant :
les coefficients du binôme de Newton équidistants des termes extrêmes sont égaux .
A partir des conclusions ci-dessus , tu peux
facilement construire
ce qu'on appelle " triangle de Pascal " ; à toi de jouer .
(groupes ciblés : terminales scientifiques)
La démonstration du binôme de Newton a supposé que les éléments x et a appartiennent à tout anneau devant vérifier un condition importante ; laquelle ?
En particulier , la formule correspondante s'applique également pour x et a appartenant à l'ensemble C des nombres complexes .
Quelques exercices
(groupes ciblés : terminales toutes séries confondues)
1) On considère un jeu de 32 cartes . On veut former des paquets de 5 cartes comprenant 4 cartes de même nom (4 as ou 4 rois , etc.) ; combien peut-on former de tels paquets ?
2) Combien y a-t-il de diagonales dans un polygone de n côtés ?
3) p est un entier naturel donné ; x et y des
entiers naturels inconnus .
Combien l'équation x + y = p admet-elle de
solutions ?
4) Une assemblée contient 20 personnes . On veut
constituer un bureau comportant un président , un secrétaire et un trésorier
.
Combien y a-t-il de façons de constituer le bureau ?
5) Dans l'alphabet il y a 26 lettres dont 6
voyelles .
Combien peut-on former de mots de 3 lettres avec deux consonnes différentes
et une voyelle , la voyelle occupant le second rang ?
6) La classe d'une institutrice est composée de 18 élèves . Combien peut-elle former des groupes de 4 élèves ?
7) On donne n points de l'espace deux à deux
distincts .
Combien peut-on tracer de droites joignant ces n points ?
Combien peut-on construire de vecteurs ayant toutes leurs extrémités choisies
parmi ces n points ?
8) Écris le développement de (x + a)n
.
En faisant x = a = 1 , calcule :
![]()
En faisant x = -a = 1, calcule :
![]()
En déduire la somme des coefficients de rang pair , ainsi que celle des coefficients de rang impair .
9) On considère les nombres de 5 chiffres
formés avec les 5 chiffres distincts :
1 , 2 3 , 4 , 5 .
Combien y a-t-il de nombres formés avec les 5 chiffres distincts précédents ?
Quelle est la somme de ces nombres ?
10) Écris le développement de (x + a)n .
En dérivant par rapport à x l'égalité
précédente , montre
que :
![]()
En intégrant , en déduire les valeurs respectives des quantités suivantes :
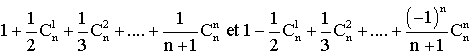
(groupe ciblé : terminale S)
1) En développant (1 + z)n par la formule du binôme de Newton puis en remplaçant z par les racines cubiques imaginaires de l'unité , calcule les sommes :
![]()
2) tu poseras :
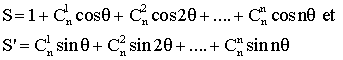
Forme S + iS' et en déduis S et S' .
dérivation et extremums d'une fonction
numérique
(groupes ciblés : terminales toutes séries
confondues)
1- Démontre que si le polynôme f(x) est
divisible par
(x - a)2 , sa dérivée f'(x) est divisible par (x - a)
et que, réciproquement, si un polynôme f(x) divisible par (x - a), a une
dérivée, elle-même divisible par (x -a), f(x) est divisible par (x - a)2
.
2- En déduire que, pour que l'équation f(x) =
0, dans laquelle f(x) est un polynôme, ait une racine double (c'est-à-dire
deux racines égales), il faut et il suffit que les deux équations :
f(x) = 0 et f'(x) = 0 aient une racine commune .
Dans tout ce qui suit, tu prendras un repère orthonormé .
3- Détermine a de façon que la courbe y = x3 - ax2 + 1 soit tangente à la droite y = 5 et construis la courbe correspondante .
4- La droite y = 5 rencontre la courbe précédente en un point A et la rencontre à nouveau au point B dont tu calculeras l'abscisse .
5- Chaque courbe y = x3 - ax2
+ 1 a un maximum et un minimum ; peux- tu le démontrer ?
On te demande de déterminer ensuite les ensembles décrits par ce maximum et ce
minimum quand le réel a varie .
une partie de billard
(groupe ciblé : terminales scientifique et
technologique)
Un billard rectangulaire (ABCD) a pour dimensions
AB = DC = a,
AD = BC = b > a . Une bille part de A et frappe successivement
les bandes [BC], [CD], [DA], en des points M, N, P .
Elle s'arrête après avoir bouclé un quadrilatère (MNPQ) .
L'angle
de réflexion est égal, chaque fois, à l'angle d'incidence .
1- Entre quelles limites doit être compris BM =
x pour que les
bandes soient frappées dans cet ordre ?
Quelle est alors la
forme du quadrilatère (MNPQ) ?
Montre que les droites supportant les côtés,
ou la diagonale
[MP], passent chacune par un point fixe .
2- Calcule en fonction de x l'aire de ce
quadrilatère .
Dans un repère orthonormé, construis le graphe de la fonction
:
![]()
Deux des circonstances suivantes peuvent-elles se
produire simultanément :
(MNPQ) rectangle, (MNPQ) losange, (MNPQ) d'aire
maximum ?
3- Calcule en fonction de l'angle BAM = t la
longueur z de la ligne brisée [AMNPQ] parcourue par la bille depuis son départ
A jusqu'à son point d'arrêt Q .

Quels sont, dans cet intervalle, les extremums de z ?
étude d'une fonction numérique et
dérivation
(groupe ciblé : terminale L)
Étudie les variations de la fonction numérique f définie par :
![]()
Représente sa courbe (C) dans un repère orthonormé et calcule l'aire comprise
entre (C) et les deux droites d'équation x = -2 et x = -1 .
homothétie et somme
(groupe ciblé : terminale S)
1- Étudie le variations de la fonction :
f(x) = 4x3 - 3x + 1
Construis le graphe (C) de f dans un repère orthonormé et montre que (C) possède un centre de symétrie .
2- Calcule l'aire comprise entre l'axe des abscisses, celui des ordonnées et l'arc de (C) sur lequel x varie de 0 à 0,5 .
3- Montre que le graphe de la fonction :
![]()
où l
est un réel
constant, se déduit de (C) par homothétie .
Quel est, lorsque l varie,
l'ensemble des points de cette courbe qui correspondent à un maximum de g(x) et
quel est l'ensemble des
points qui correspondent à un minimum ?
4- Étudie les variations de la fonction :
![]()
Construis sa courbe représentative et indique quelles sont les tangentes à cette courbe aux points qui ont pour abscisses -1 et 0,5 .
5- Calcule cos 3f en
fonction de cos f.
Tu utiliseras la relation obtenue
et le changement x = cos f
pour trouver les racines de l'équation :
![]()
exponentielle
(groupes ciblés : terminales toutes séries
confondues)
Calcule la dérivée de la fonction numérique : y = (n - x) ex , où n est une constante réelle .
Étudie, quand x est un réel largement positif,
les variations de la fonction : y = (2 - x) ex
et en construis la courbe représentative
pour
ces valeurs de x dans un repère orthonormé .
Calcule l'aire du domaine compris entre cette
courbe et les
demi-axes [Ox et [Oy .
un peu de cinématique
(groupes ciblés : terminales S
et techno.)
1- calcule la dérivée de e-x .
![]()
les coordonnées d'un point M sont données
en fonction
de l'instant t par les formules :
x = et , y = e-t , où t prend toute valeur réelle .
Construis la trajectoire, (C), du point M .
3- Donne les coordonnées du vecteur-vitesse et
du
vecteur-accélération du point M à l'instant t .
![]()
vecteur-vitesse de M à l'instant t; construis la courbe (H) décrite
par m;
compare (H) et (C) .
5- On considère sur (C) le point M à un instant
quelconque t;
![]()
que M' est sur (Ox) .
![]()
un peu de la métrique dans
un triangle
(groupes ciblés : première et terminale S)
On te donne dans un plan fixe deux points
distincts et fixes E et F. On pose |EF| = a, a réel strictement positif.
Dans ce plan, un point M mobile se déplace tel que
ME2 + MF2
= k2 , avec k réel constant dont la valeur absolue est différent de
0.
Trouve le lieu géométrique de M (c'est-à-dire la trajectoire que décrit M ou encore
l'ensemble des points M), en te servant de la notion de produit scalaire.
Pour t'aider dans ton raisonnement, ouvre la page animation 2.
tu as dis ellipse ?
(groupe ciblé : terminale S)
Première partie : la notion fondamentale de l'ellipse.
On te donne dans un plan fixe deux points
distincts et fixes A et B.
Un point M mobile de ce plan se déplace tel que |MA| + |MB| = k, k étant une
constante réelle strictement positive.
Trouve le lieu géométrique du point M.
Pour t'aider dans ton raisonnement, ouvre la page animation 3.
Deuxième partie : une autre définition de l'ellipse.
On te donne dans un plan fixe une droite (d') fixe et un point A fixe n'appartenant pas à (d').
Un point M de ce plan se déplace tel que le rapport de |MA| à |MH|, H étant la projection orthogonale de M sur (d'), soit égal à une constante réelle k tel que 0 < k < 1.
Trouve le lieu géométrique du point M.
Pour t'aider dans ton raisonnement, ouvre la page:
Troisième partie : transformé d'un cercle par affinité orthogonale.
On te donne dans un plan fixe un cercle quelconque de diamètre fixe [AB].
Trouve le transformé de ce cercle par l'affinité orthogonale d'axe (AB), la droite support de [AB], et de rapport constant le réel k, |k| étant différente de 0 et de 1.
Pour t'aider dans ta recherche, ouvre la page animation 5.
une petite révision à nos L
(groupe ciblé : terminale L)
Première partie
Un sac contient 12 boules blanches et 8 boules rouges. Tu tires 4 boules de ce sac.
1) Quel est le nombre de cas possibles ?
2) Quel est le nombres de cas favorables à l'obtention de 3 boules blanches et une boule rouge ? En déduire la probabilité correspondante.
Deuxième partie
Soit l'équation dont l'inconnue est x et où m est un paramètre réel, définie par :
![]()
On te
demande de résoudre graphiquement cette équation, en fonction des valeurs
que peut prendre m.
Représente graphiquement la fonction numérique g définie par :
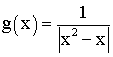
Dans cette partie le repère sera orthonormé.
Troisième partie
Quelle est la nature de la suite des fractions :
![]()
Vers quelle limite tend la somme des termes de cette suite infinie de fractions ?
Quatrième partie
Résous dans R2 le système suivant :
x + y = 65
log x + log y = 3
Je te rappelle que le symbole log (avec un "l" minuscule) est celui des logarithmes décimaux.