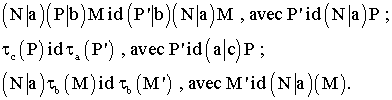La notion de théorie sera au fur et à mesure explicitée le long de la présente .
Pour fixer les idées , soit une théorie mathématique quelconque que
NON NOVA , SED NOVE ...........(page
1)
(cette page est exclusivement dédiée à toutes celles
et tous ceux qui souhaitent approfondir leurs connaissances en mathématique ;
son contenu n'est inscrit dans aucun des programmes du collège et du
lycée)
1-Mathématique formelle
1-1-Notions de termes et de relations
1-1-1-Signes et
assemblages d'une théorie mathématique
La notion de théorie sera au fur et à mesure explicitée le long de la présente
.
Pour fixer les idées , soit une théorie mathématique quelconque que
![]()
-
les
lettres d'un alphabet ; pour fixer les idées on prendra les lettres
de
l'alphabet latin minuscules ou majuscules , affectés ou non
d'accents ; par
exemple A , B , A' , B" , x , y' , z" , etc.
![]()
Un assemblage de la théorie de T est
une suite de signes de T et
dans laquelle certains des signes différents des lettres peuvent être joints
deux à deux par des liens .
A titre d'exemple , la suite suivante :
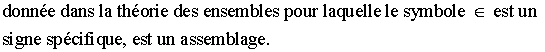

Le respect de ce
formalisme aboutit très vite à des écritures d'assemblages trop longues et
compliquées . Ainsi , on utilisera des
![]()
Par exemple , les symboles
suivants représentent des assemblages trop longs s'il fallait les écrire
formellement :
![]()
![]()
![]()
On donne un assemblage A et une lettre y .

![]()
Soient A , B deux
assemblages et x une lettre .
L'assemblage obtenu en remplaçant x en chacune de ses occurrences dans A , par
l'assemblage B , sera écrit de la façon suivante :
![]()
qui se lira " B remplace x dans A " .
![]()
![]()
Dans tout ce qui suit , et par convention , nous écrirons "A id B" pour dire que l'assemblage A est identique à l'assemblage B .
1-1-2-Critères de substitution
Premier critère
Soient M , N deux assemblages , a et a' des lettres .
![]()
![]()
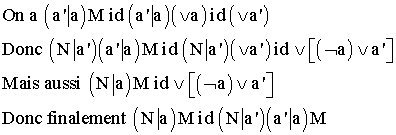
Deuxième critère
Soient M , N , P trois assemblages , a et b des lettres distinctes.
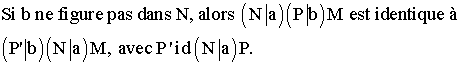
![]()
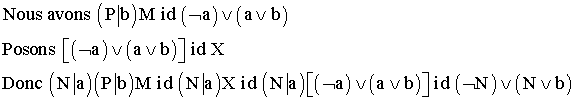
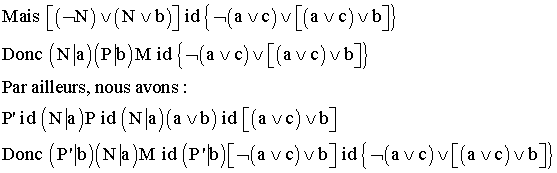
![]()
Troisième critère
On donne M un assemblage ; a , a' deux lettres .
![]()
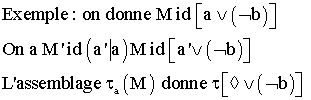
----
![]()
----
![]()
Quatrième critère
On donne deux assemblages M , N ; a , b deux lettres distinctes .
![]()

---------
![]()
--------
---------
---------
![]()
-------
![]()
Cinquième critère
Soient M , N , P des assemblages , a une lettre .
Les assemblages suivants :

sont identiques respectivement aux assemblages :
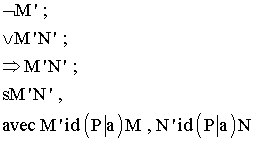
Exemple : on donne les assemblages M , N , P suivants :
![]()
A titre d'exercice , et avec cet exemple, vérifie ce dernier critère.
Deux autres exercices
1- On donne les
assemblages suivants :
![]()
![]()
![]()
2- En reprenant les assemblages M , N , P pris en exemples pour vérifier le cinquième critère ci - dessus , montre que l'on a :