Il sera dit de deuxième espèce dans les autres cas .
NON NOVA , SED NOVE ...........(page
2)
(cette page est exclusivement dédiée à toutes celles
et tous ceux qui souhaitent approfondir leurs connaissances en mathématique ;
son contenu n'est inscrit dans aucun des programmes du collège et du
lycée)
1-1-3 Constructions formatives
On associe à chaque signe spécifique un nombre
entier naturel, appelé son poids .
Ce nombre est pratiquement toujours égal à 2 .
Un assemblage sera dit de première espèce s'il
commence par
![]()
Il sera dit de deuxième espèce dans les autres cas .
Une
construction formative d'une théorie T est une suite d'assemblage
possédant la propriété suivante :
pour chaque assemblage A de la suite, l'une des conditions suivantes est
vérifiée :
a- A est une lettre,
b- Il y a, dans la suite, un assemblage de deuxième espèce B
![]()
c-
Il y a, dans la suite, deux assemblages de deuxième espèce B
![]()
d- Il y a, dans la suite, un assemblage de
deuxième espèce B
![]()
e- Il y a un signe spécifique s de poids n de T , et n assemblages de première espèce A1 , A2 , ... , An précédant A dans la suite, tels que A soit sA1A2...An
On appelle termes de T les assemblages de première
espèce figurant dans les constructions formatives de T .
On appelle relations de T les assemblages de deuxième espèce
figurant dans les constructions formatives de T .
Exemples :
Dans la théorie des ensembles que tu noteras E,
où le signe :
![]()
Que peut être le poids de ce signe ?
On te donne la suite d'assemblages S1 suivante définie dans E :
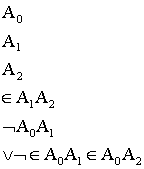
Est-elle une construction formative ? Justifie ta réponse .
On te donne dans E la suite S2 suivante :

Est-elle une construction formative dans E ? Justifie ta réponse .
Donne dans E deux exemples de construction formative .
Quelques remarques :
1) Quelques auteurs réservent aux mots " terme " et " relation " respectivement les mots " objet " et " assertion " ; ainsi une relation est une assertion que l'on peut faire sur des objets .
2) La condition b de la propriété que doit
vérifier une construction

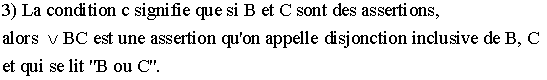
4) L'assertion suivante :
![]()
est appelée implication logique et se lit
" A implique logiquement B " ou encore " A entraîne B " .
![]()
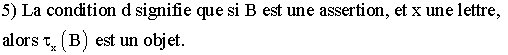
Supposons que l'assertion B
exprime une propriété de l'objet x .

6) La condition e signifie que si A1 , A2 , A3 , ... , An sont des objets, et s un signe spécifique de poids n, alors s A1 A2 A3 ... An est une assertion relative aux objets A1 , A2 , A3 , ... , An .
Exercice
Parmi les énoncés qui suivent lesquels sont vrais ? Justifie tes réponses

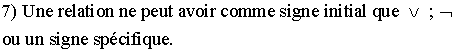
![]()
1-1-4 Critères formatifs
Les quatre critères qui suivent peuvent être facilement établis
Premier critère formatif :
![]()
Deuxième critère formatif :
![]()
Troisième critère formatif :

Quatrième critère formatif :
si A1 , A2 , A3 , ... , An sont des termes d'une théorie T et si s est un signe spécifique de poids n de T, alors sA1A2A3...An est une relation de T .
A partir des quatre critères ci-dessus, tu pourras établir facilement les six qui suivent :
Cinquième critère formatif :
![]()
Sixième critère formatif :
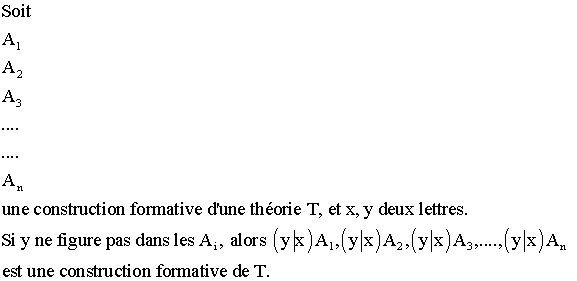
Septième critère formatif :

Huitième critère formatif :
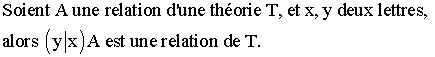
Neuvième critère formatif :
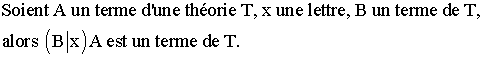
Dixième critère formatif :
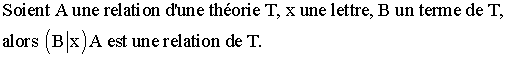
1.2 Axiomes et théorèmes d'une théorie
1-2-1 Axiomes d'une théorie
Les signes spécifiques d'une théorie T nous ont
permis d'y définir des termes et des relations .
Pour achever la construction de T, nous allons procéder de la manière suivante
:
1) On énonce d'abord un certain nombre de relations de T . On dira que ces
relations sont des axiomes explicites de T ; les lettres qui figurent
dans ces axiomes sont les constantes de T .
2) On se munie d'une ou de plusieurs règles, qu'on appelle les schémas
de T .
Ces schémas doivent présenter les particularités suivantes :
- l'application d'une règle R fournit une relation de T ;

Toute relation formée par application d'un
schéma ou d'une règle de T est appelée " axiome implicite de T "
.
1-2-2 Démonstrations dans une théorie
Une démonstration (on dit encore " texte démonstratif ") d'une théorie T se compose :
- d'une construction formative auxiliaire de
termes et de relations
de T ;
- d'une suite de relations de T figurant dans la
construction formative auxiliaire, telles que, pour chaque relation A de la
suite, l'une au moins des conditions suivantes soit vérifiée :
* A est un axiome explicite de T
* A résulte de l'application d'un schéma de T à des termes ou
relations figurant dans la construction formative auxiliaire
* il y a dans la suite deux relations B, C précédant A, telles
que
![]()
Toute relation figurant dans une démonstration de T est appelée théorème de T .
Parfois un théorème de T peut également s'appeler relation vraie de T, ou proposition de T, ou lemme de T, ou encore corollaire de T .
Soit A une relation de T, x une lettre, B un terme de T.
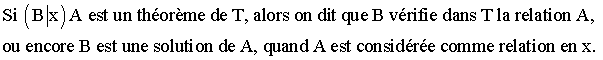
Une relation est dite fausse dans T
si sa négation est un théorème de T .
On dit qu'une théorie T est contradictoire quand on y énonce une relation simultanément vraie et fausse .
Dans ce qui suit, tu aborderas l'ensemble des critères dits " critères de substitution " permettant d'abréger les démonstrations . Ils sont précédés de symboles tels que CSi .
Exercice
On te donne A et B deux relations d'une théorie T.
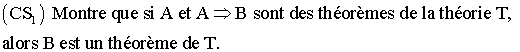
Ce critère que tu viens de démontrer permet d'abréger les démonstrations ; il s'appelle " syllogisme ".
1-2-3 Substitutions dans une théorie
Soient T une théorie, A1 , A2 , A3 , ... , An ses axiomes explicites, x une lettre, B un terme de T .
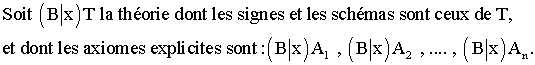

(CS3 )
Soient A un théorème de T, x une lettre qui
n'est pas une constante de T .
![]()
Ce critère découle du premier ci-dessus .
1-2-4 Comparaison des théories
Une théorie T' est dite plus forte qu'une théorie T si tous les signes et schémas de T sont des signes et schémas de T' et si tous les axiomes explicites de T sont des théorèmes de T' .
(CS4 )
Si une théorie T' est plus forte qu'une théorie T, alors tous les théorèmes
de T sont des théorèmes de T' .
(CS5 )
Soient T une théorie, A1 , A2 , A3
, ... , An ses axiomes explicites,
c1 , c2 , c3
, ... , ck ses constantes, B1 , B2 , B3
, ... , Bk des termes de T .
![]()
soient des théorèmes d'une théorie T', que les
signes et schémas de T
soient les signes et schémas de T' .
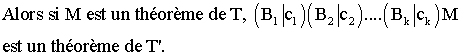
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la terminale L (page 4)
L'exercice pour la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)