L'EXERCICE
POUR
LA TERMINALE S
(page 7)
les thèmes abordés dans cette page
étude d'une fonction numérique, complexes et rotation, calcul d'intégrales
![]()
Partie A

Partie B
![]()
A tout point M du plan d'affixe z, la rotation r
associe le point M' d'affixe z'.
1-
1-a
Donner z' en fonction de z.
On note z = x + iy et z' = x' + iy' (x, x', y, y' étant des réels); exprimer
x' et y' en fonction de x et y, puis exprimer x et y en fonction de x' et
y'.
1-b
Déterminer les coordonnées des points A', B', et P' images respectives des
points A, B et P par r.
2-

Partie C
Rappel : l'image d'un domaine plan par une rotation est un domaine plan de même aire.

solution
Partie A
1-
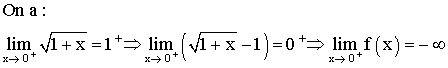
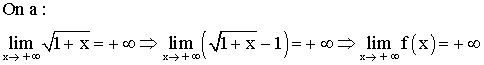
2-
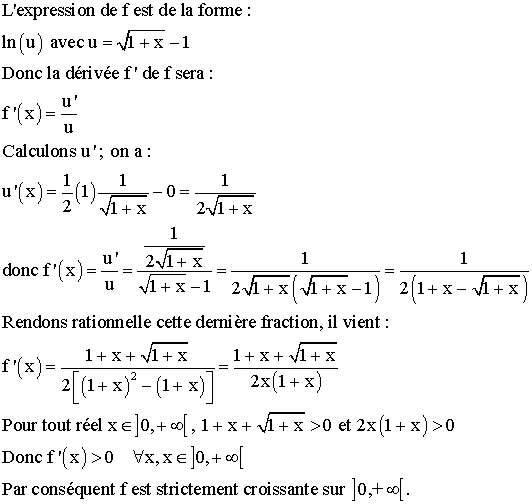
3-
Construisons (C).
Le tableau de variation de f est :
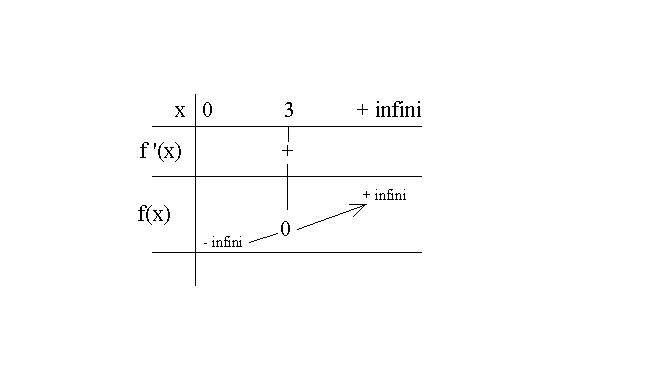
3-

La courbe représentative (C) de f est :
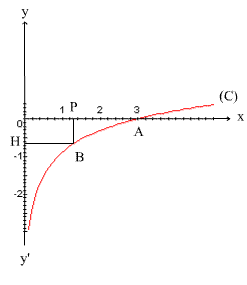
Partie B
1-
a- Soit M un point quelconque du plan et z son affixe.


b- D'après la première partie, on a :
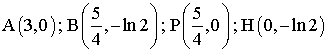
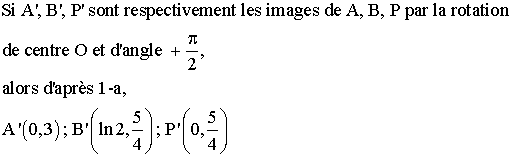
2-
a-
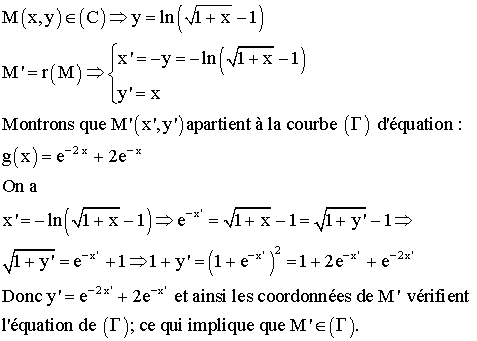
b- Les résultats obtenus au 2-a nous permettent de tracer la courbe
représentative de g et de placer les points A', B'.
On obtient le graphique suivant :
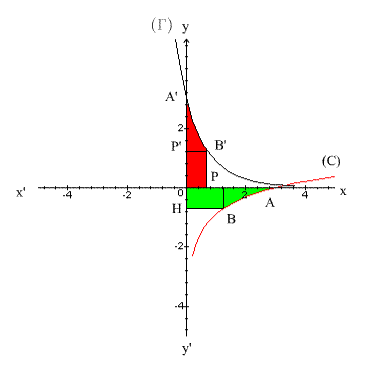
Partie C
1-
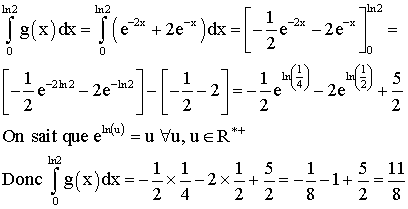
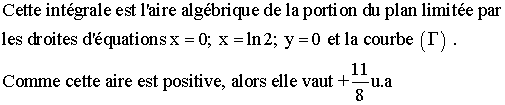
2-

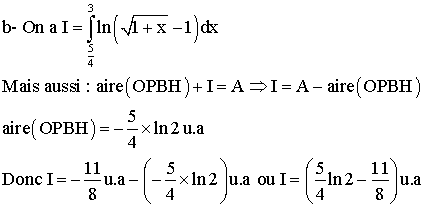
page 1 page 2 page 3 page 4 page 5
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)