"SOS MATH" est dédié à toutes celles et tous ceux qui préparent des concours ou examens ; quelques passages dépassent les programmes du Collège ou du Lycée . Il est également dédié à toute personne intéressée par l'application des mathématiques à divers domaines des sciences physiques ou de la matière .
les thèmes abordés dans cette page
équation de la chute d'un corps
éprouvant dans sa chute une résistance de l'air
équation de la chute d'un corps
éprouvant dans sa chute une résistance de l'air
On laisse tomber un corps de
masse m d'une certaine hauteur .
On te demande d'établir la loi de variation de la vitesse de chute v sachant
que ce corps éprouve pendant sa chute une résistance de la part de l'air proportionnelle à la vitesse .
Le coefficient de proportionnalité de la résistance de l'air par rapport à la
vitesse v est le réel strictement positif k .
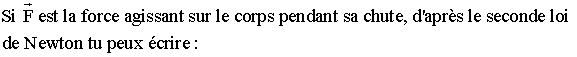
![]()

L'équation devient :
![]()
Ainsi, en y isolant les termes portant sur v, tu
obtiens :
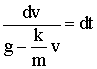
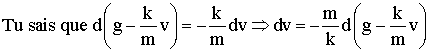
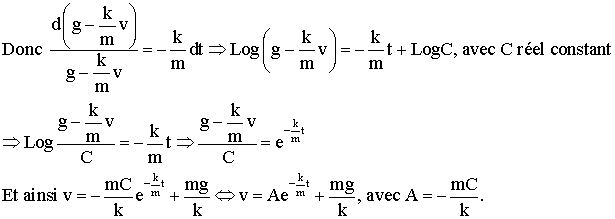
Tu
obtiens ainsi la solution générale de l'équation différentielle posée au
départ .
Il existe donc une infinité de solutions , et à chaque valeur
du paramètre réel A correspond une solution au problème posé .
On suppose qu'à l'instant t = 0 , le corps solide est lâché à la vitesse initiale v0 . Trouve la solution particulière sachant que la résistance de l'air est négigeable.
Si k = 0 (résistance de l'air nulle)
, alors l'équation différentielle
devient :
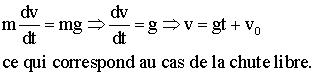
La vitesse de désintégration du
radium est directement proportionnelle à sa masse à l'instant considéré .
Déterminons la loi de variation de sa masse en fonction du temps , sachant
qu'à l'instant t = 0 la masse était m0 .
La vitesse de désintégration se détermine comme suit :

Nous avons ainsi :
![]()
Cette limite s'appelle vitesse d'intégration du radium .
D'après les données du problème , nous avons :
![]()
k est le coefficient de proportionnalité .
Nous avons pris -k car la masse décroît
lorsque le temps t croît et par
![]()
Séparons les variables dans notre équation :
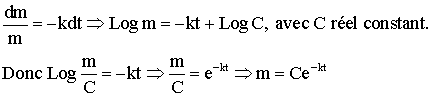
La condition initiale étant pour t = 0 , m = m0 , nous obtenons finalement :
![]()
1- Déduis k sachant que la
fraction de la masse initiale désintégrée dans le temps t0 est de a % .
2- On a établi par cette méthode que pour le radium ,
k vaut 0,000436 ,
l'unité de temps étant l'année .
Trouve la période de désintégration du radium , c'est-à-dire le laps de
temps pendant lequel la moitié de sa masse initiale sera désintégrée .
Tu devras trouver T = 1590 ans .
On te donne dans un plan fixe une droite fixe (d) et un point F fixe n'appartenant pas à (d).
Dans ce plan un point M mobile se déplace tel que si H est sa projection orthogonale sur (d), le rapport de |MF| à |MH| reste constant et égal à k, k étant un réel strictement supérieure à 1.
Trouve la trajectoire que décrit M (lieu géométrique de M) par la méthode de la géométrie analytique, en choisissant adéquatement le repère orthonormé.
Pour t'aider dans ton raisonnement, ouvre la page animation 9.
Reprends l'exercice pour chacun des cas suivants : k = 1 ; 0 < k < 1
page 2 page 3 page 4 page 5 page 6