
"SOS MATH" est dédié à toutes celles et tous ceux qui préparent des concours ou examens ; quelques passages dépassent les programmes du Collège ou du Lycée . Il est également dédié à toute personne intéressée par l'application des mathématiques à divers domaines des sciences physiques ou de la matière .
le thème abordé dans cette page
câbles ou fils électriques
câbles ou fils électriques
Un câble électrique supposé
flexible et homogène est suspendu à ses deux extrémités .
Trouvons à l'équilibre l'équation de la courbe décrite par ce câble .
On nous donne g le poids spécifique du câble .
Soit S le point le plus bas
du câble .
Définissons comme repère orthonormé plan celui dont l'origine
w est la
projection orthogonale de S sur le plan horizontale du lieu de cote 0 .
L'axe
des ordonnées sera celui des cotes : [wS , dont le sens ascendant est le
sens positif ; l'axe des abscisses sera [wx , contenue dans le plan du câble et
perpendiculaire à [wS .
Posons z0 l'ordonnée de S ; ainsi S (0 ; z0 ) .
Soit M un point arbitraire différent de S sur ce
câble . Considérons la portion (SM) de ce câble . Cette dernière est en
équilibre sous l'action de trois forces :

![]()
la composante horizontale égale à T.cosf ;
la composante verticale égale à T.sinf .
Ainsi à l'équilibre , nous devons avoir :
T.cosf = H et T.sinf = gs
.
d'où
![]()
Si y = f(x) est l'équation de la courbe recherchée , alors nous devons avoir :
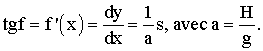
Dérivons les deux membres de cette égalité par rapport à x , nous obtenons :
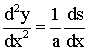
Mais nous savons que :
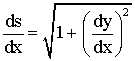
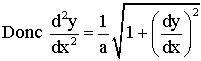
Arrêtons-nous sur cette équation
différentielle qui est de la forme :
y'' = f (x ; y') .
Nous allons établir la méthode générale de sa
résolution , ceci avant de retourner au cas particulier de notre problème .
![]()
Ainsi nous avons :
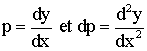
L'équation y'' = f (x ; y') s'écrit alors :
![]()
Cette dernière équation est du premier ordre
et p est une
fonction de x .
Nous obtenons par intégration sa solution générale p = p (x ; C1)
, et ainsi :
![]()
Appliquons cette méthode à notre problème en
posant y' = p .
L'équation devient alors :
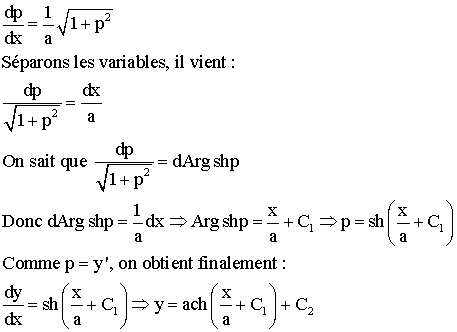
La dernière égalité ci-dessus est la solution générale de notre équation différentielle . Les paramètres réels C1 et C2 étant fixés, sa courbe représentative dans notre repère orthonormé s'appelle chaînette .
Sachant que la condition initiale
du problème est : x = 0 entraîne
[y = b et y' = 0 (point le plus bas du
câble)] , trouve la solution particulière .
page 1 page 2 page 3 page 4 page 6