"SOS MATH" est dédié à toutes celles et tous ceux qui préparent des concours ou examens ; quelques passages dépassent les programmes du Collège ou du Lycée . Il est également dédié à toute personne intéressée par l'application des mathématiques à divers domaines des sciences physiques ou de la matière .
le thème abordé dans cette page
volume d'un tronc de cylindre
volume d'un tronc de cylindre
Soit dans l'espace un repère
orthonormé (O ; i ; j ; k) .
L'unité prise sur les axes est le centimètre .
On te donne un tronc de cylindre dont la base circulaire a pour rayon 1 cm et
pour équation dans ce repère , x2
+ y2 = 1 . La face supérieur appartient à un plan
d'équation
x + 2y + z - 8 = 0 .
Détermine le volume de ce tronc .
La base circulaire définit dans le plan z = 0 un
domaine régulier que nous appellerons D .
Soit V le volume recherché .
Nous avons :
![]()
Ce qui donne :
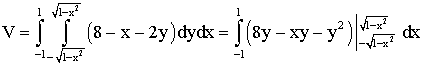
Calculons l'expression sous la somme ; nous obtenons :
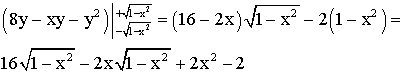
D'où V est la somme de trois intégrales que nous allons calculées séparément :
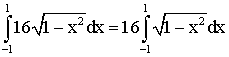
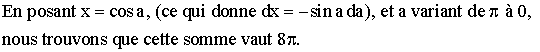
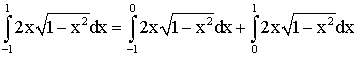
En posant 1 - x2 = u (ce qui donne -2xdx = du) et u variant de 0 à 1 pour x allant de -1 à 0 , puis de 1 à 0 pour x variant de 0 à 1, nous trouvons que cette somme est nulle .
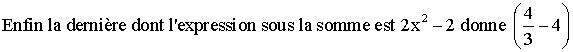
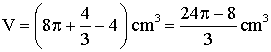
page 1 page 3 page 4 page 5 page 6