"SOS MATH" est dédié à toutes celles et tous ceux qui préparent des concours ou examens ; quelques passages dépassent les programmes du Collège ou du Lycée . Il est également dédié à toute personne intéressée par l'application des mathématiques à divers domaines des sciences physiques ou de la matière .
le thème abordé dans cette page
volume d'un corps solide compris entre une
sphère
et une surface cylindrique
volume d'un corps solide compris entre une
sphère
et une surface cylindrique
Trouvons le volume V du corps
compris entre la sphère d'équation : x2 + y2 + z2
= 4a2
et la surface cylindrique d'équation : x2 + y2 - 2ay = 0
.
Le repère (O ; i ; j ; k) pris dans l'espace est
orthonormé et l'unité de mesure des longueurs est le mètre .
Nous prendrons comme domaine d'intégration D l'intersection de la surface cylindrique et du plan du repère d'équation z = 0 , c'est-à-dire le cercle d'équation x2 + y2 - 2ay = 0 .
Cette dernière peut également s'écrire : x2 + (y-a)2 = a2 .
Calculons le quart du volume V recherché en prenant pour domaine d'intégration D' le demi-cercle défini par les équations :
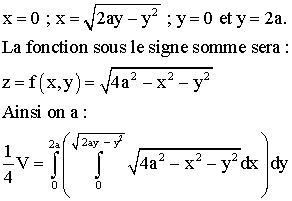
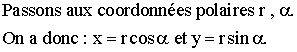

La frontière du domaine en coordonnées polaires est telle que :
![]()
La fonction à intégrer devient :
![]()
Nous obtenons finalement :
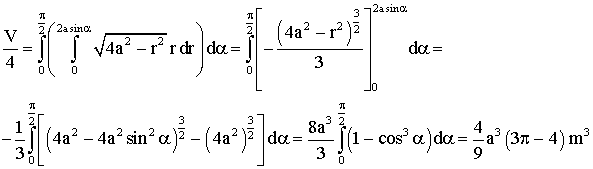
![]()
page 1 page 2 page 4 page 5 page 6