L'EXERCICE POUR LA TERMINALE S
(page 4)
les thèmes abordés dans cette page
existence et signe des racines d'une équation
f est une fonction numérique définie sur R – {-1} par :
![]()
![]()
Soit le point A(-1;2).

1)
En utilisant l’égalité vectorielle :
![]()
trouver les formules de changement de variable.
2)
![]()
3)
En déduire que Cf a un centre de symétrie dont on précisera les coordonnées.
Solution
Pour déterminer les
propriétés d’une courbe souvent le changement de repère est commode.
Ainsi pour montrer qu’une courbe C possède un axe de symétrie ou un centre de symétrie, généralement on fait subir au repère dans lequel C a été construite une translation vectorielle.
Si f est la fonction numérique
représentée par C dans l’ancien repère, alors dans le nouveau repère, C
représentera une nouvelle fonction numérique g que l’on doit déterminer.
Ainsi, c’est à l’aide de g que l’on pourra déterminer les propriétés de C.
Par souci de simplification appelons R0 l’ancien repère et R1 le nouveau.
![]()
1)
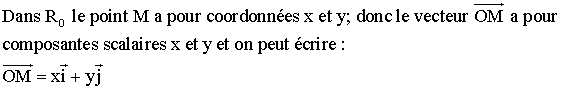

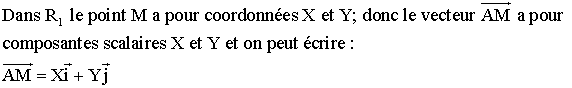
Ainsi on obtient l’équivalence logique suivante :
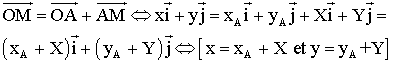
Les formules de changement de variables, ceci en passant de R0 à R1 sont données par le système :
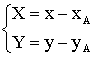
Avec
xA = -1 et yA = 2, on obtient donc :
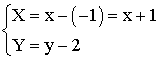
2)
L’équation de Cf dans le repère R1 s’obtient en remplaçant dans
l’expression :
![]()
y et x par leurs valeurs respectives en fonction
de X et Y.
Ainsi :
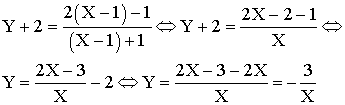
Dans le repère R1 , la courbe Cf représente donc la fonction numérique g définie par :
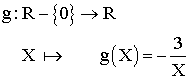
![]()
3)
Dans le repère R1 on a :
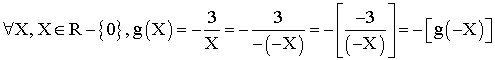
Donc dans ce repère d’origine A, g est une
fonction impaire et la courbe Cf admet
A pour centre de symétrie ; de plus on sait que les coordonnées de A
dans l’ancien repère R0 sont xA
= -1 et yA = 2.
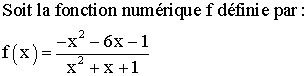
1)
Montrer que f est définie sur R.
2)
a-
Simplifier l'expression f(x)-4
b-
Montrer
que 4 est le maximum de f(x).En quelle valeur de x est-il
atteint ?
3)
a-
Montrer que f(x) + 3 > 0
b-
Que peut-on en déduire ?
Solution
1)
Le dénominateur est un trinôme du second degré en x.

2)
a-
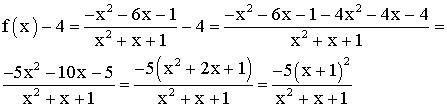
b-
Dans f(x) – 4 , le dénominateur, ayant un discriminant strictement négatif, est du même signe que son a = 1 pour tout réel x; donc il est
strictement positif pour tout réel x.
![]()
Ainsi :
![]()
Ce qui implique que f admet dans R un
maximum qui est égal à 4.
Ce maximum est atteint pour la valeur de x telle
que f(x) = 4 ou
f(x) – 4 = 0
Ainsi :
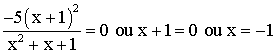
f atteint son maximum 4 pour la valeur de x égale à –1
3)
a-
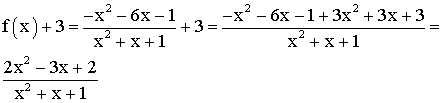
On sait déjà que le dénominateur est
strictement positif pour tout réel x.
Le numérateur est un trinôme du second degré en x.
![]()
Il est donc du signe de son a = 2 pour tout réel
x ; c’est-à-dire il est strictement positif pour tout réel x.
Conclusion :
![]()
b-
Ainsi on a :
![]()
Donc f est bornée sur R.
De plus f est continue sur R.
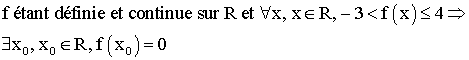
existence et signe des racines d'une équation
Discuter suivant les valeurs du paramètre réel m l’existence et le signe des racines réelles de l’équation :
![]()
Solution
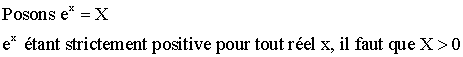
L’équation devient :
![]()
Posons d le discriminant de cette équation.
Soient, lorsque les racines existent, s et p respectivement la somme et le produit de ces racines.
L’existence de racines réelles dépend du signe de d. Calculons d et étudions son signe en fonction du paramètre m.

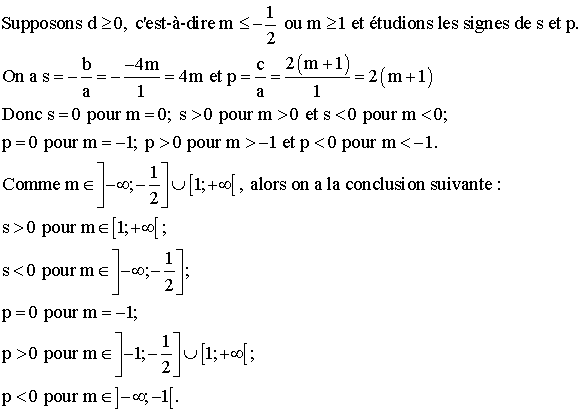
Comme X doit être strictement positive, donc :
![]()
alors on a la conclusion générale établie par le
tableau suivant :

L’équation
proposée admet :

On considère le polynôme
![]()
1)
Calculer sa valeur pour z = z1 = 2 + 3i
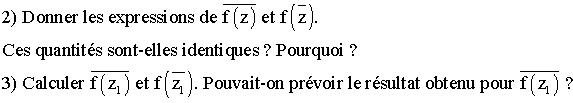
solution
1)
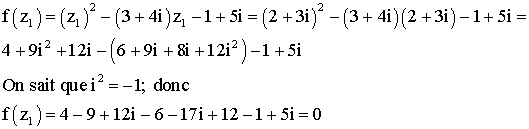
2)
Rappel du cours

![]()
Cela
résulte du fait que les coefficients du polynôme f(z) sont des nombres
complexes et non des réels.
![]()
que
si f est un polynôme ou une fraction rationnelle à
coefficients réels.
3)
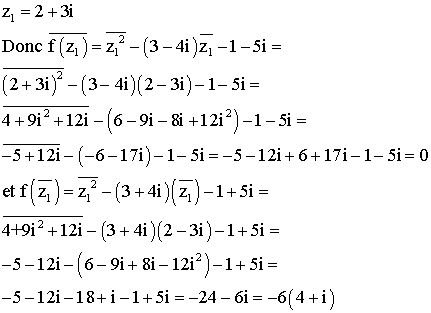
![]()
page 1 page 2 page 3 page 5 page 6 page 7