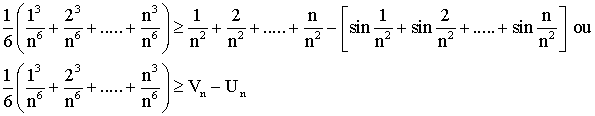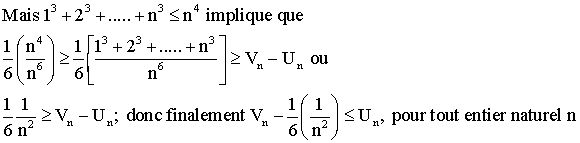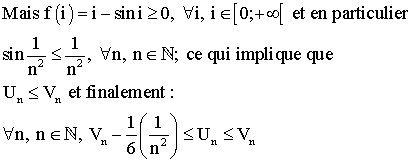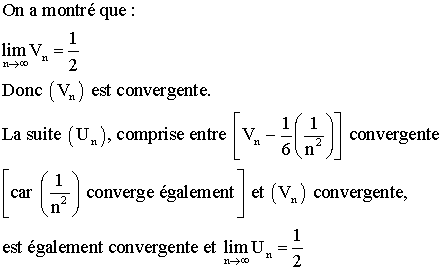les nombres complexes et le plan complexe
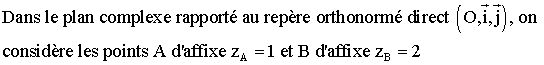
(unité
graphique 4 cm)
![]()
L'
EXERCICE POUR LA TERMINALE S
(page 2)
les thèmes abordés dans cette page
les nombres complexes et le plan complexe
suites
numériques et convergence ; trigonométrie
les nombres complexes et le plan complexe
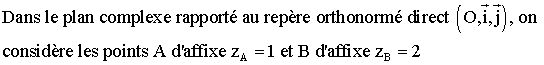
(unité
graphique 4 cm)
![]()
![]()
1)
Montre que le point M appartient au cercle C de centre A et de rayon 1.
2)
![]()
En déduis-en l'ensemble E des points M quand q décrit ]0,π[
![]()
z' l'affixe de M'.
![]()
Puis montre que M' appartient à C.
4)
![]()
![]()
Soit A' l'image de A par r.
a-
Définis l'image C' du cercle C par r.
Place sur une figure A, B, C, M, C' puis le point M' image de M par r.
b-
Montre que le triangle (AMO) est équilatéral.
c-
Montre C et C' se coupent en O et en M'.
d-
Soit le point P symétrique de M par rapport à A.
Montre que M' est le milieu de [A’P].
Solution
1)
On a
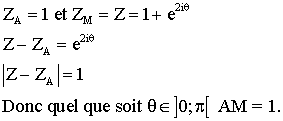
Donc M est sur le cercle de centre A et de rayon 1.
2)
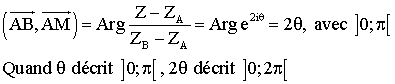

3)
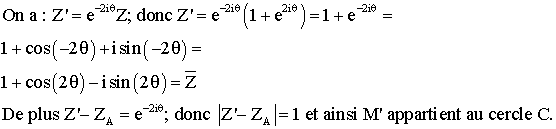
4)
a-
On sait que dans une rotation, l'image d'un cercle est un cercle de même
rayon.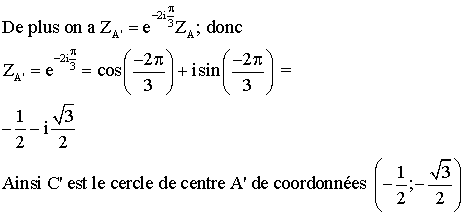
et de rayon 1.
D’où la figure suivante :
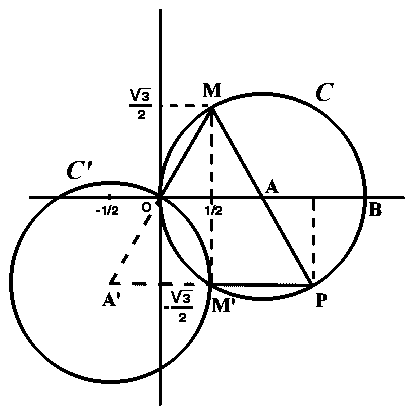
b-

c-

d-

suites numériques et convergence ; trigonométrie
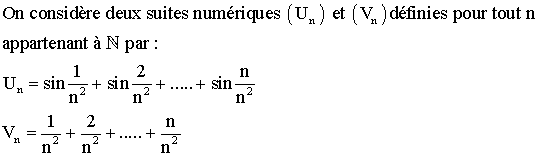
![]()
b)
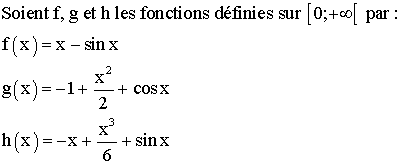
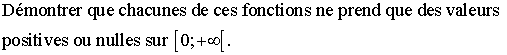
Justifier que :
![]()
Démontrer que :

Solution
a)

b)
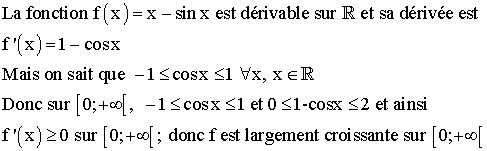
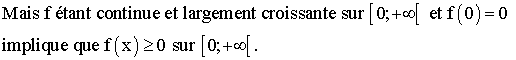
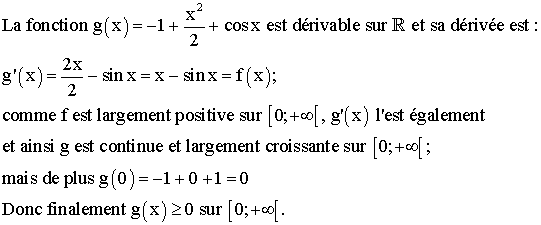
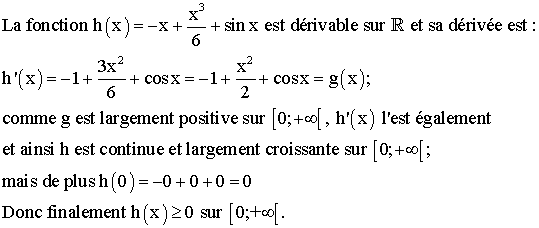
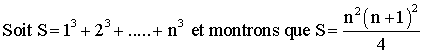
La relation est vraie pour
les rangs n=1, n=2, n=3 ; supposons-la vraie pour
(n-1) et démontrons qu’elle reste vraie pour n.
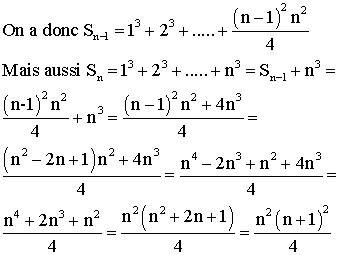
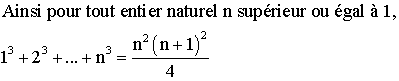
![]()
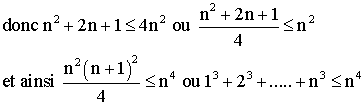
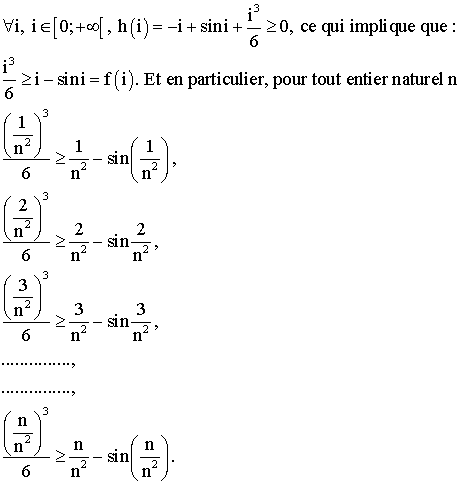
Additionnons membre à membre,
il vient: