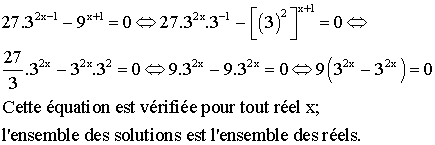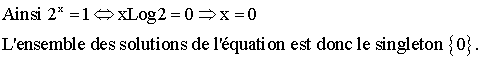L'EXERCICE POUR LA TERMINALE S
(page 5)

les thèmes abordés dans cette page

calcul d'une aire algébrique 

fonction a^x 

résolution d'équations contenant des termes de la forme a^x 

calcul d'une aire algébrique 

Calculer l’aire algébrique :

solution

retour au début de la page

fonction a^x 

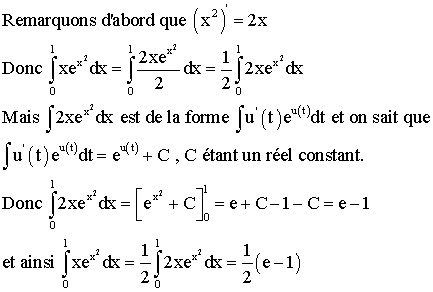
On donne la fonction numérique f définie par :

1- Étudier les variations de f.

2- Représenter graphiquement f dans un repère orthogonal (unités : 1 cm sur l’axe des abscisses et 0,5 cm sur l’axe des ordonnées). Soit C la courbe représentative de f.

Écrire l’équation de la tangente à C au point où cette dernière rencontre l’axe des ordonnées.

3- Calculer l’aire de la portion du plan limitée par C, l’axe des abscisses et les deux droites d’équations x = 0 et x = 1.

Calculer l’aire géométrique de la portion du plan limitée par C, l’axe des abscisses et les deux droites d’équations x = 0 et x = -1.

4- Calculer la quantité :

retour au début de la page

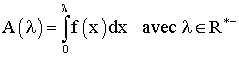
solution

1-

Le domaine de définition de f est R .

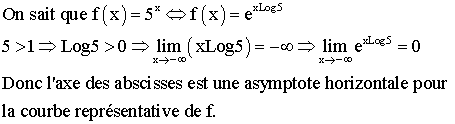
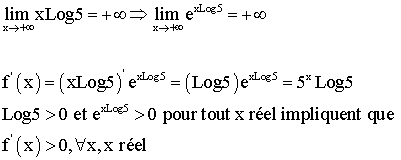
D’où le tableau de variation de f :

2- 

Construction de la courbe C représentative de f :

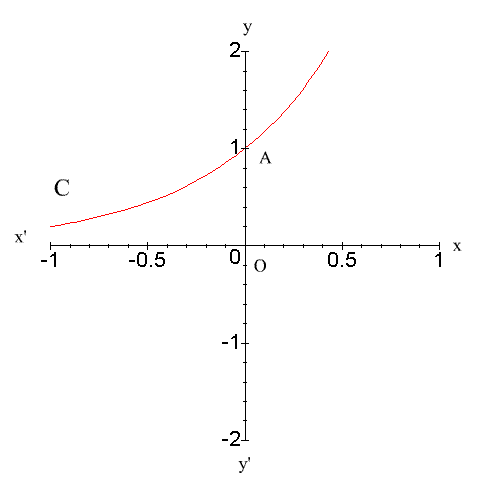
Soit A le point d’intersection de C et de l’axe des ordonnées.

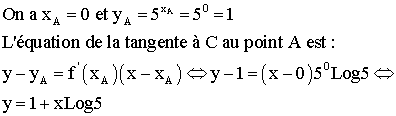
3- 

Soit u.a l’unité d’aire correspondante aux unités prises sur les axes des coordonnées.

Posons s l’aire de la portion du plan comprise entre la courbe C, l’axe des abscisses et les deux droites d’équation x = 0 et x = 1.

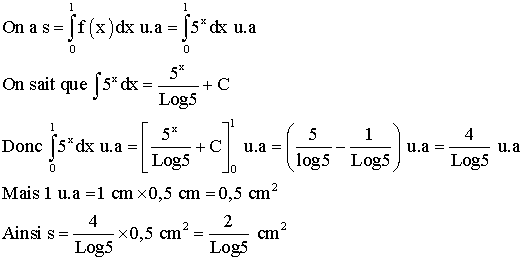
Posons S l’aire de la portion du plan comprise entre la courbe C, l’axe des abscisses et les deux droites d’équation x = 0 et x = -1.

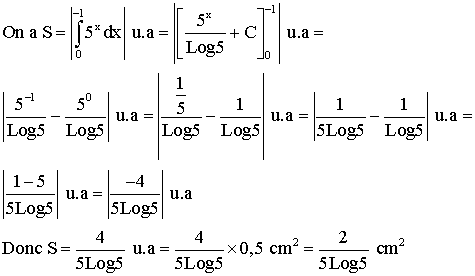
4-

retour au début de la page

résolution d'équations contenant des termes de la forme a^x 

1)

Résoudre dans R² le système suivant :

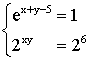
solution

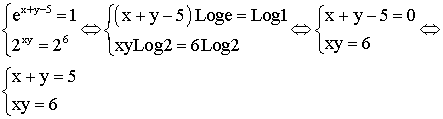
x et y sont les racines d’une équation du second degré dont la somme et le produit des racines sont respectivement S = 5 et P = 6.
Cette équation est :

retour au début de la page

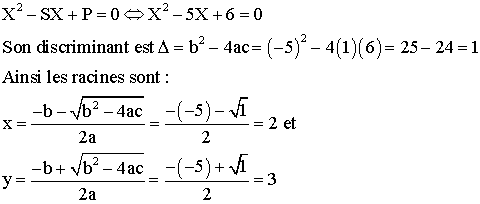
2)

Résoudre dans R les équations :

solutions

retour au début de la page

page 1          page 2          page 3          page 4         page 6       

page 7