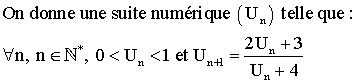
Démontrer que cette suite est croissante et convergente.
L'EXERCICE POUR LA TERMINALE S
(page 3)
les
thèmes abordés
monotonie
d’une suite numérique ; convergence
barycentre
d’un système de points de l’espace
condition
d’alignement de trois points et nombres
complexes
équation du type y’ = ay ( a réel différent de 0)
monotonie
d’une suite numérique ; convergence
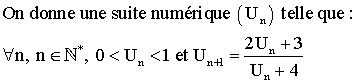
Démontrer que cette suite est croissante et convergente.
Donc
Un est différent de 0 et on peut diviser les deux membres de l’égalité
définissant la suite par Un . On obtient :
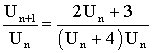
Dans le second membre mettons Un en facteur, au numérateur ; et,
puisque Un est différent de 0, simplifions par Un , on obtient:
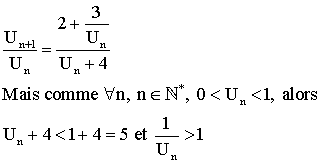
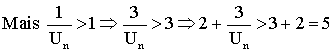
Ainsi :
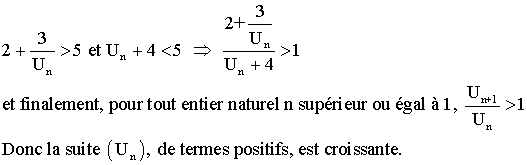
Par
ailleurs on connaît le théorème très important :
Toute suite numérique croissante (resp. décroissante) et majorée (resp. et minorée) est convergente.
Appliquons ce théorème à notre cas particulier.
On
a :

barycentre
d’un système de points de l’espace
Soient trois points de
l'espace A, B, C non alignés et soit k un réel de
l'intervalle [-1;1].
{(A , k²+1) , (B , k) , (C , -k)}
a-
![]()
b-
![]()
2)
Déterminer l'ensemble E des points M
de l'espace tels que :
![]()
Solution
1)
a-
Pour tout réel k de
l'intervalle [-1;1], on a :
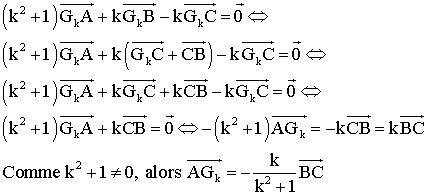
b-
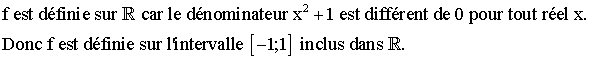
Par ailleurs, f est dérivable
sur [-1 ;1] et sa dérivée est égale à :
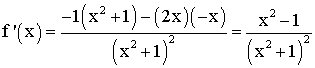
f ’(x) est du signe de son
numérateur ; donc f ’(x) est largement négative
![]()
On a montré que f définie
sur [-1;1] est décroissante dans cet intervalle ;
![]()
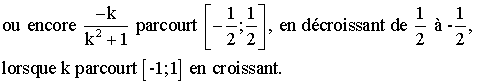
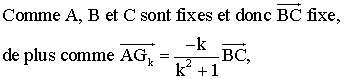
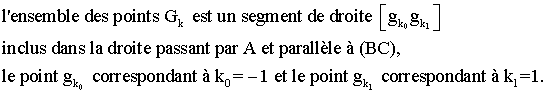
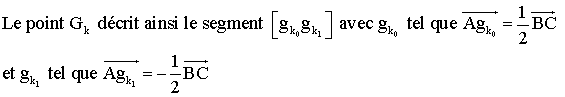
2)
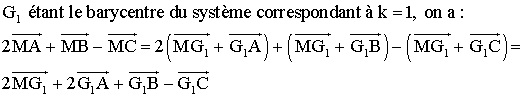
![]()
et
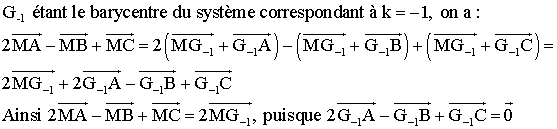
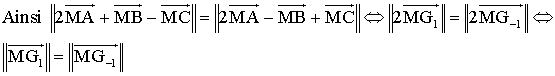
Ainsi, comme les points G1
et G-1 sont fixes, l'ensemble E des points M de l'espace est le plan
médiateur du segment fixe [G1 G-1]
NB: dans le plan, l'ensemble E
des points M sera la médiatrice du segment [G1 G-1].
condition d’alignement de trois points et nombres complexes
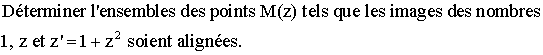
solution
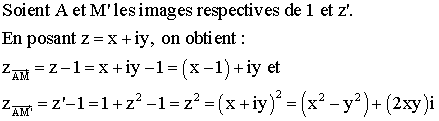
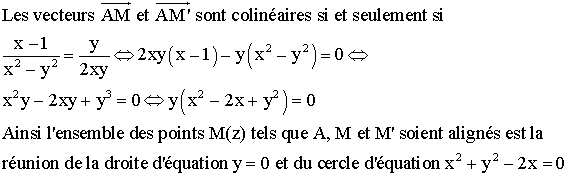
Explicitons le cercle.
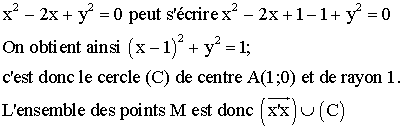
équation du type y’ = ay ( a réel différent de 0)
Partie 1
On considère l’équation différentielle
suivante :
![]()
1)
Donner la solution générale de cette équation.
2)
Déterminer
celle des solutions qui prend la valeur 1 pour x = 0. Montrer que cette solution
peut se mettre sous la forme :
![]()
Partie 2
On considère l’équation différentielle
suivante :
![]()

Rappel du cours
Pour résoudre de telles équations on procède par séparation
des variables.

solution
Partie 1
1)
L’équation (1) peut se mettre sous la forme :
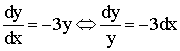
Ainsi,
en intégrant les deux membres :
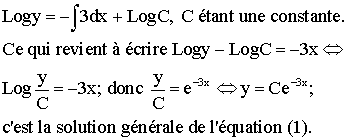
Pour x = 0, y = 1 ; donc
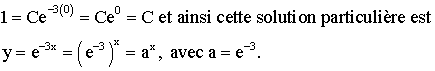
Partie 2
1)


ou
![]()
2)
