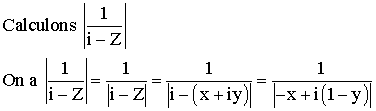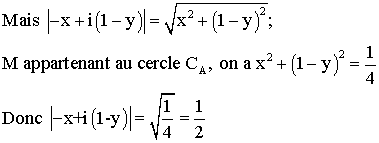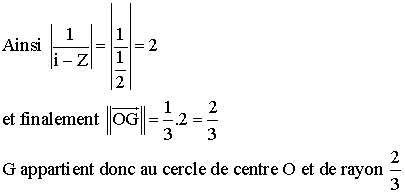
L'EXERCICE POUR LA TERMINALE S
(page 1)
le
transformations dans le plan complexe et géométrie vectorielle
transformations dans le plan complexe et géométrie vectorielle
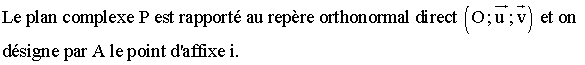
A tout point M du plan, distinct de A, d'affixe Z, on associe le point M' d'affixe Z' défini par:
![]()
1)
Déterminer
les points M confondus avec leur image M'
2)
Étant donné un complexe Z distinct de i, on pose Z = x + iy et
Z' = x' + iy'
avec x, y, x', y' réels.
3)
Trouver
une relation simple liant les longueurs OM, AM et OM' ; en déduire
l'ensemble F des points M du plan tels que M et M' soient situés sur un même
cercle de centre O.
4)
Dans
cette question, on considère un point M d'affixe Z, situé sur le cercle de
centre A et de rayon 1/2. M' est le point d'affixe Z' correspondant, et G l'isobarycentre
des points A, M et M'.
Calculer
l'affixe ZG de G en fonction de Z.
Montrer
que G est situé sur un cercle de centre O dont on précisera le rayon.
1)
D’abord
l’équation :
![]()
n’a
de sens que si i – Z est différent de 0 ; donc il faut que Z soit différent
de i, c’est-à-dire il faut que les points M soient différents de A.
Cette
condition étant remplie, posons :
![]()
équation
que doivent vérifier les points M confondus avec leurs images (M’ = M ou Z’
= Z).
Cette
équation devient, puisque i – Z est différent de 0 :
![]()
En
mettant Z en facteur, on obtient :
![]()
Ainsi
les solutions de cette équation sont :
![]()
donc les points M se confondant avec leurs images sont

2)
Avec
Z = x + iy et Z’ = x’ +iy’, l’équation s’écrit :
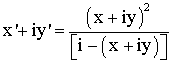
Donc
on aura :
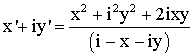
Mais
on sait que i2 = -1 ; d’où
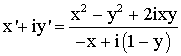
Multiplions
le numérateur et le dénominateur du second membre par le
conjugué
du dénominateur [-x + i(1-y)] qui est égal à [-x – i(1-y)] ; on
obtient :
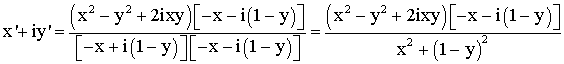
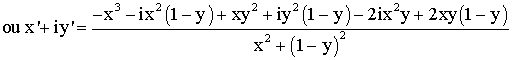
Ainsi
on obtient :
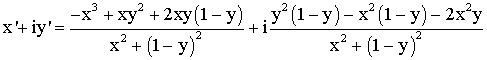
En
identifiant les parties réelles, on obtient :
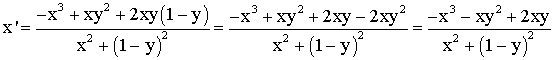
et
en mettant x en facteur dans le numérateur :
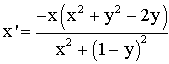
Un
point appartient à l’axes des imaginaires purs si et seulement si la partie réelle
de son affixe est nulle.
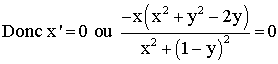
Comme
Z est différent de ZA = i, le dénominateur est différent de 0 et
ainsi :
![]()
![]()
L'ensemble
des points M tels que leurs abscisses soient nulles est l'axe des imaginaires
purs privé de A. Appelons (d) cet ensemble.
Trouvons
l’ensemble des points M tels que x2 + y2 – 2y = 0
On
sait que (y - 1)2 = y2 – 2y + 1 ; donc y2 –
2y = (y - 1)2 – 1 et ainsi
![]()
L’ensemble
des points M tels que x2 + y2 – 2y = 0 est donc le
cercle de centre
A et de rayon 1. Appelons (C) cet ensemble.
Conclusion :
L’ensemble
des points M dont l’image M’ appartient à l’axe des imaginaires purs est :
![]()
3)
![]()

De
plus on sait que :
![]()
La
relation donnée par hypothèse est :
![]()
Ainsi on a :
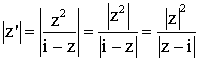
Les
points M de P tels que M et M’ appartiennent à un cercle centré sur O doivent
satisfaire la relation :
![]()
D’où
l’équation :
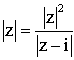
Comme
z est différent de i, il vient :
![]()
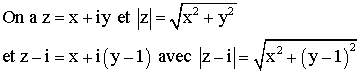
L’équation
s’écrit donc :
![]()
ou
encore
![]()
en
élevant au carré, il vient :
![]()
On
peut simplifier par x2 + y2 puisque les points M sont
différents
de O, centre du cercle, et donc x2 + y2 est différent de
0.
On obtient donc :
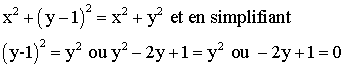
L’ensemble
F des points M tels M et M’ appartiennent à un cercle centré sur O est donc
la droite d’équation –2y + 1 = 0
4)
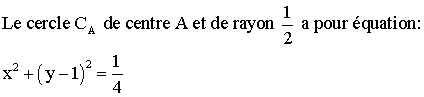
Les
cordonnées de M doivent donc vérifier cette équation.
G
étant l'isobarycentre des points A, M et M', on a :
![]()