Quelle est la nature de cette transformation composée ?
L'
EXERCICE POUR LA SECONDE ET LA PREMIERE S
(page 4)
les thèmes abordés dans cette page
composition
de transformations géométriques
(2de)
droites et plans perpendiculaires
(2de)
division d'un polynôme P(x) par (x -
a)
(1ère S)
projection sur un plan et lieux géométriques
(1ère S)
composition
de transformations géométriques
(groupe
ciblé : seconde)
Partie 1
On
donne dans un plan (P) deux points distincts O et O’.
![]()
![]()
Quelle est la nature de cette transformation composée ?
La composition des symétries centrales est-elle commutative ?
Partie
2
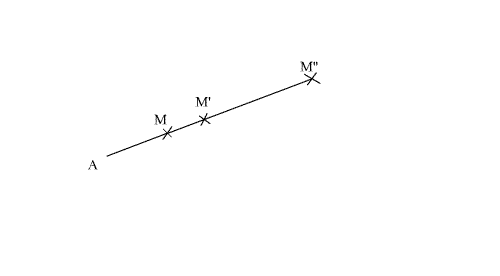
On
donne dans (P) un point A quelconque différent de O et O’.
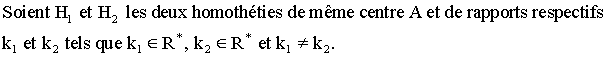
![]()
La
composition des homothéties est-elle commutative ?
On
donne un trapèze quelconque (ABCD).
Les diagonales [AC] et [BD]
se coupent en O et les deux côtés non parallèles [AD]
et [BC],
en I.
Soient M et N les milieux respectifs des deux côtés [AB]
et [DC].
En choisissant deux homothéties adéquates, montre que les points I, M, O et N
sont alignés.
Solution
Partie
1
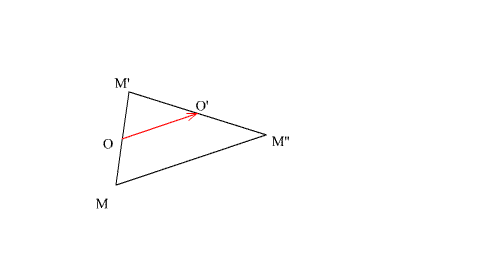
Soit
un point M quelconque de (P), différents de O et O’.
![]()
![]()
On
a :
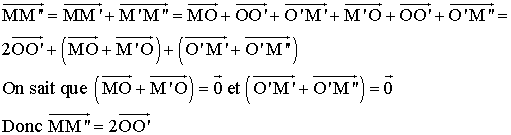
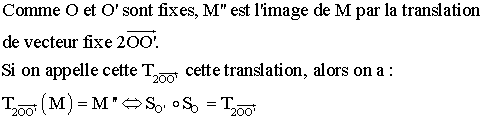
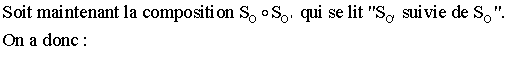
![]()
![]()
On
a :
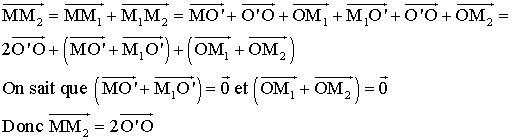

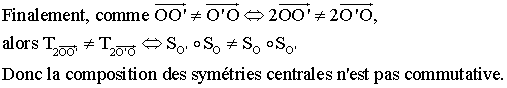
Partie
2
![]()
On
a :

![]()
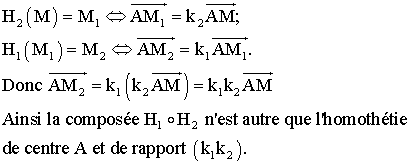

On
donne maintenant un trapèze quelconque (ABCD).


droites et plans perpendiculaires
(groupe ciblé : seconde)
Partie
1
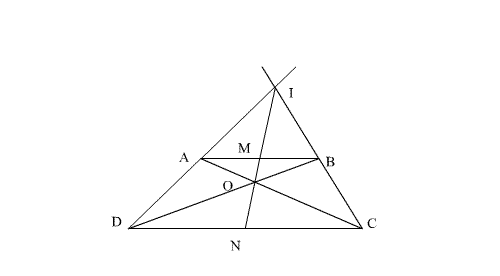
On
donne une droite (d) et un point O de l’espace n’appartenant pas à (d).
Soient (Q) un plan variable contenant (d) et H le pied de la perpendiculaire menée
de O au plan (Q).
Quel
est, lorsque (Q) varie, l’ensemble des droites (OH) ?
Quel est l’ensemble des points H ?
Partie
2
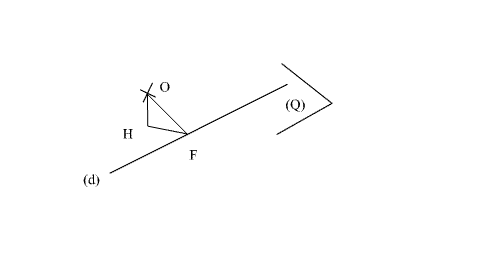
On considère,
dans un plan P, un cercle (C) de diamètre [AB]. Soient M un point variable de
ce cercle et S un point fixe de la droite (D) perpendiculaire en A à P.
On
mène de A les perpendiculaires [Ax
et [Ay
respectivement à [SB]
et [SM].
[Ax
rencontre [SB]
au point E et [Ay
rencontre [SM]
au point F.
1)
Montre que (BM) est perpendiculaire à (SM).
2)
Montre que (AF) et (SE) sont respectivement perpendiculaires aux plans (SEF) et
(AEF).
3)
Quel est l’ensemble des points F lorsque M décrit (C) ?
4)
Quel est l’ensemble des points F lorsque, M restant fixe, le point S décrit
(D) ?
Solution
Partie
1
Abaissons
de O la perpendiculaire à (d) qui coupe cette dernière en F.
O et (d) étant fixes, alors F l’est également.
(OH)
étant orthogonale à (Q), est orthogonale à toute droite de (Q) et en
particulier à (d).
(OH)
étant perpendiculaire à (d) et (OF) étant perpendiculaire à (d), alors (d)
est perpendiculaire à deux droites concourantes du plan (OHF) et ainsi (d) est
orthogonale au plan (OHF).
Le
plan (OHF) passe par le point fixe O et est orthogonal à la droite fixe (d) ;
donc (OHF) est fixe.
L’ensemble des droites (OH) est donc le plan (OHF).
(OH)
étant orthogonale à (Q) est orthogonale à toute droite de (Q) et en
particulier à (HF).
Dans
le plan fixe (OHF), O et F sont fixes. De plus, (OH) est perpendiculaire à
(HF).
Donc, l’ensemble des points H est le cercle inclus dans le plan fixe (OHF) et
de diamètre fixe [OF].
Partie 2
1)
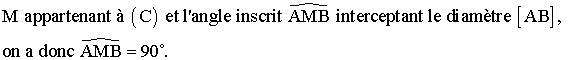
Par
ailleurs, (D) ou (AS) est orthogonale au plan (P) ; donc (AS) est
orthogonale à toute droite incluse dans (P) et en particulier à (BM).
Ainsi,
(BM) étant perpendiculaire à (AM) et à (AS), donc perpendiculaire à deux
droites concourantes du plan (AMS), est perpendiculaire au plan (AMS).
(BM) étant perpendiculaire au plan (AMS), est perpendiculaire à toute droite
incluse dans ce plan et en particulier à (SM).
2)
(BM)
étant perpendiculaire à deux droites concourantes (SM) et (AM) du plan (SAM),
est perpendiculaire à ce plan ; donc(BM) est perpendiculaire à toute
droite de ce plan et en particulier à (AF).
(AF)
étant perpendiculaire à deux droites concourantes (BM) et (SM) ou (SF) du plan
(SMB) ou (SEF), est perpendiculaire à ce plan.
(AF)
étant orthogonale au plan (SEF), est perpendiculaire à toute droite de ce plan
et en particulier à (SE).
(SE)
étant perpendiculaire aux deux droites concourantes (AE) et (AF) du plan (AEF),
est orthogonale à ce plan.
3)
(SB)
et A étant fixes, le plan (SAB) est fixe. Dans ce plan, la droite (Ax) passant
par le point A fixe et perpendiculaire à (SB) fixe, est fixe ; donc son
intersection E, avec (SB) fixe, est fixe.
Le plan (AEF) passant par E fixe et perpendiculaire à (SE) fixe est fixe.
(AF) étant orthogonale au plan (SEF), est orthogonale à toute droite de ce
plan et en particulier à (EF).
Donc, dans le plan fixe (AEF), A et E étant fixes et (AF) étant
perpendiculaire à (EF), l’ensemble des points F est le cercle inclus dans le
plan fixe (AEF) et de diamètre fixe [AE].
4)
(AF)
étant orthogonale au plan (SEF), est orthogonale à toute droite de ce plan et
en particulier à (SF) ou (FM)
division d'un polynôme P(x) par (x -
a)
(groupe
ciblé : première S)
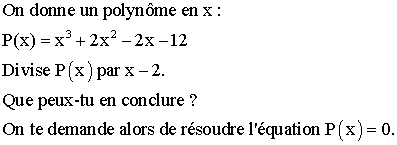
Solution

Le
dividende n’est autre que P(x) développé selon les puissances décroissantes
de x.
On
divise le monôme de P(x) ayant la plus grande puissance par rapport à x,
ici x3 , par x. On obtient x2 comme premier terme du
quotient.
Ensuite, on effectue le produit x2 (x – 2), puis on procède à
ajouter au dividende, ici P(x), l’opposé de ce produit qui est –x3
+ 2 x2 .
Le résultat de cette addition, après simplification, est :
4x2 – 2x – 12.
On
divise le monôme de plus grande puissance de ce résultat par rapport à x, ici
+4x2 , par x.
On obtient +4x comme second terme du quotient.
Ensuite, on effectue le produit 4x(x – 2), puis on procède à ajouter à
4x2 – 2x –12, l’opposé de ce produit qui est – 4x2
+ 8x .
Le résultat de cette addition, après simplification, est :
6x – 12.
On
divise le monôme de plus grande puissance de ce résultat par rapport à x, ici
+6x , par x.
On obtient +6 comme troisième terme du quotient.
Ensuite, on effectue le produit 6(x – 2), puis on procède à ajouter à 6x
–12, l’opposé de ce produit qui est –6x + 12.
Le résultat de cette addition, après simplification, est : 0x + 0 ;
c’est finalement le reste de cette division.
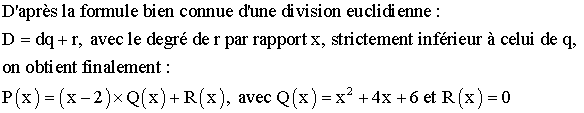
Ce
qui montre donc que P(x) est divisible par x – 2 .
L’équation
P(x) = 0 peut donc s’écrire :
![]()
On
vérifie si le second facteur x2 + 4x + 6 peut être factorisé. Ce
n’est pas le cas ici car l’équation x2 + 4x + 6 = 0, ayant un
discriminant 16 – 24 strictement négatif, n’admet pas de racines réelles,
et donc x2 + 4x + 6 ne peut se mettre sous la forme : a(x – x1
)(x – x2 ), avec x1 et x2
ces racines.
Finalement
on a :
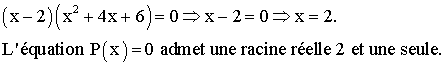
projection sur un plan et lieux géométriques
(groupe
ciblé : première S)
On considère
dans l’espace deux plans parallèles P et P’ et un point fixe O appartenant
à P.

1
- Trouve l’ensemble des points N lorsque M est fixe.
2
- Trouve l’ensemble des points M lorsque N est fixe.
3
- Trouve l’ensemble des points M et celui des points N lorsque la droite (MN)
varie en passant constamment par un point fixe S de l’espace n’appartenant
ni à P, ni à P’.
Solution
1 -
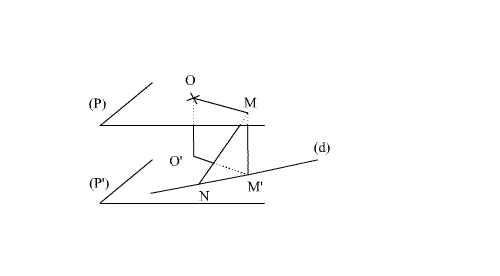
Soit
M’ le projeté orthogonal de M sur le plan (P’). M étant fixe, alors M’
l’est également.

Dans
(P’), O’ et M’ étant fixes et (NM’) étant perpendiculaire à (O’M’),
l’ensemble des points N est donc la droite (d) passant par M’ fixe et
perpendiculaire à la droite fixe (O’M’).
2 -

Soit
N’ le projeté orthogonal de N sur le plan (P). N étant fixe, alors N’
l’est également.
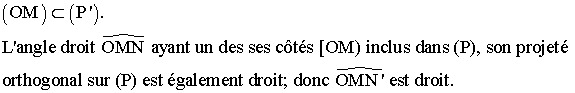
Dans (P), O et N’ étant fixes et (OM) étant perpendiculaire à (MN’), l’ensemble des points M est le cercle de diamètre fixe [ON’].
3 -
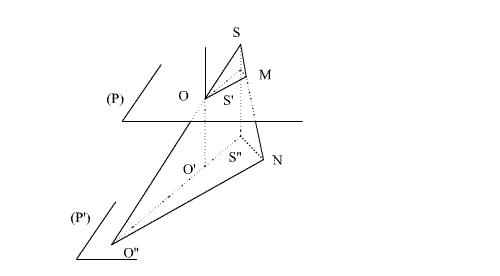
De S
menons la perpendiculaire commune à (P) et (P’) qui les coupe respectivement
en S’ et S’’.
(P),
(P’) et S étant fixes, cette perpendiculaire l’est également, ainsi que
S’ et S’’.
Soit
la perpendiculaire commune à (P) et (P’) passant par O. Elle rencontre (P’)
au point O’. (P), (P’) et O étant fixes, cette perpendiculaire l’est également,
ainsi que O’.
Les
plans (SOM) et (SOS’) ont la droite (SO) comme intersection et cette droite
coupe (P’) en O’’. Comme (P’), S et O sont fixes, alors O’’ l’est
également.
Le plan (SOM)
rencontre les plans parallèles (P) et (P’) en deux droites parallèles (OM)
et (O’’N).
Le plan (SOS’) rencontre les plans parallèles (P) et (P’) en deux droites
parallèles (OS’) et (O’’S’’).
Le
plan (SS’M) rencontre les plans parallèles (P) et (P’) en deux droites
parallèles (S’M) et (S’’N).

Trouvons
donc l’ensemble des points M.
(OM) est perpendiculaire à (MN) ou (SM).

page 1 page 2 page 3 page 5 page 6