
L'EXERCICE
POUR LA SECONDE ET LA PREMIERE S
(page 3)
les thèmes abordés dans cette page
fonction trigonométrique,
résolution d'inéquations trigonométrique et symétrie axiale
(1ère S)
fonction
numérique et détermination du maximum d'une quantité
(1ère S)
fonction trigonométrique,
résolution d'inéquations trigonométrique et symétrie axiale
(groupe ciblé : première S)
On
considère la fonction f définie sur R par f(x) = 2 sin x + cos 2 x
Soit Cf sa courbe représentative dans un repère
orthogonal.

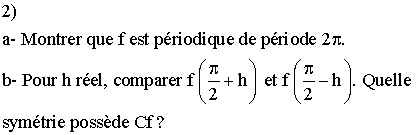
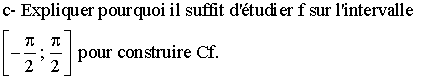
3)
a- Calculer la dérivée f ' (x) et la factoriser à
l'aide la formule
trigonométrique.
b- Étudier
le signe de f '(x) et en déduire les variations de f sur
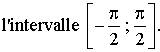
![]()
4)
En déduire que la fonction f est bornée sur R.
Rappel de cours
Fonction périodique
Soit f une fonction numérique de domaine de définition Dom(f).
f est dite périodique de période T appartenant à R si et
seulement si :
![]()
Symétrie axiale
Soit
f une fonction numérique de domaine de définition Dom(f).
Soit
dans un repère orthogonal (non nécessairement normé), Cf la courbe représentative
de f.
On dira que Cf admet pour axe de symétrie la droite (d) d’équation
x = a, avec a appartenant à Dom(f) si et seulement si :
![]()
Dérivées
des expressions f(x) = sin (ax + b) et g(x) = cos (ax + b)
f ’(x) = a cos (ax + b) et g ’(x) = -a sin (ax + b).
1)
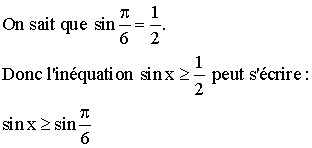
Soit
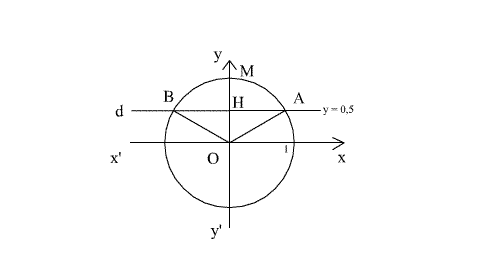
un cercle trigonométrique (C) de centre O et de rayon 1 ; l’axe (x’Ox)
est celui des cosinus et l’axe (y’Oy) qui est perpendiculaire à
(x’Ox) est celui des sinus ; de plus le repère (x’x , y’y)
est considéré orthonormé d’unité 1.
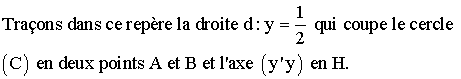
On
a donc :
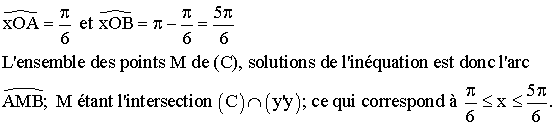
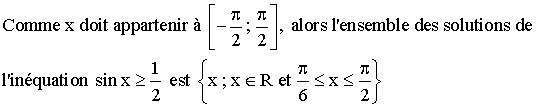
2)
a-
On a pour tout réel x :
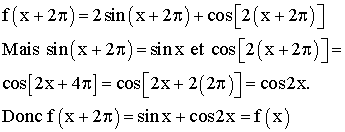
![]()
b-
Soit
h réel quelconque. On a :
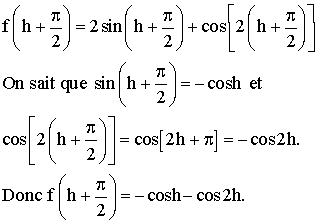
Par ailleurs,
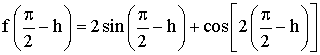
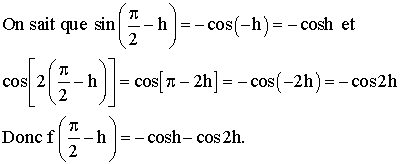
Conclusion :
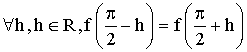
Soit
M point de Cf d’abscisse :
![]()
Considérons le point M’ de Cf d’abscisse :
![]()
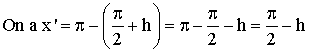
D’après
la conclusion ci-dessus, f(x) = f(x’) ou encore :
![]()
Cf
admet donc pour axe de symétrie la droite (D) d’équation :
![]()
c-
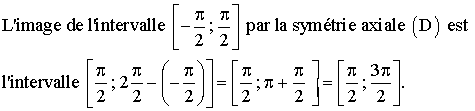
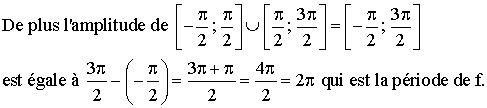
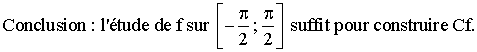
3)
a-
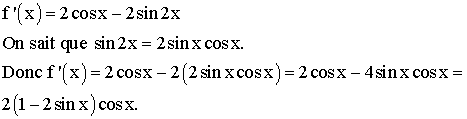
b-
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un au moins de
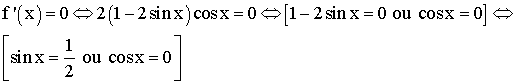
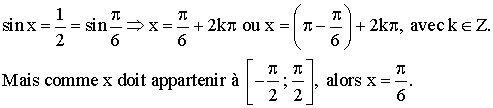
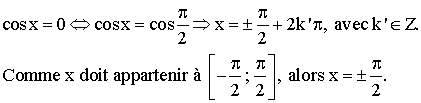
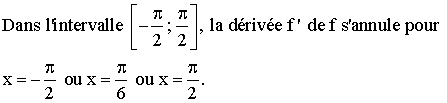
D’après
la question 1) on a :
![]()
Mais aussi et sur le
cercle trigonométrique précédent, on a :
![]()
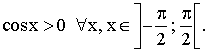
Conclusion :
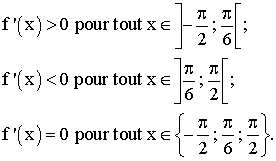
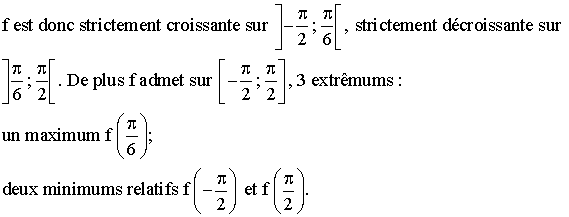
c-
Construction de Cf.
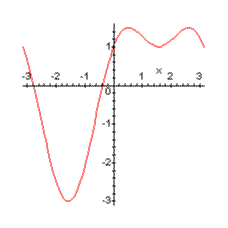
4)
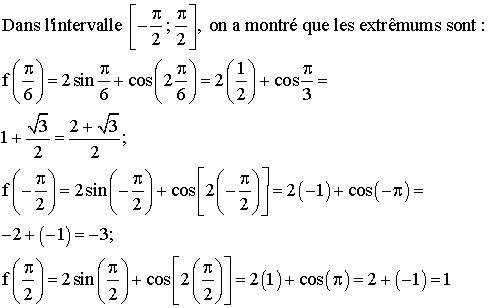
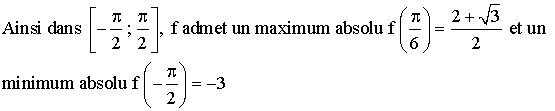
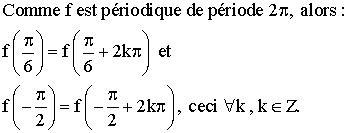
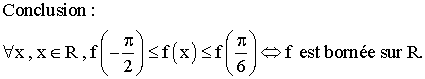
fonction
numérique et détermination du maximum d'une quantité
(groupe ciblé : première S)
Tu
es à la direction de la propreté d’une collectivité territoriale et tu
envisages d’implanter sur les trottoirs des sphères qui contiendront des
poubelles cylindriques.
La
direction de la voirie t’impose dans ce cas un maximum de 6 dm pour le rayon
de la sphère, ceci pour ne pas perturber la continuité du cheminement piéton.
On suppose qu'une poubelle a pour hauteur h et rayon r (en dm).
Tu
dois déterminer la hauteur du cylindre pour obtenir une poubelle de volume
maximal.
Exprime
r en fonction de h.
a-
Démontre que le volume V du cylindre en dm3 peut s'écrire sous la
forme :
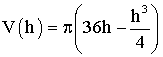
b-
Étudie les variations de la fonction V.
a-
Détermine la hauteur du cylindre pour laquelle le volume de la
poubelle est maximal.
b-
Détermine la valeur exacte de ce volume en dm3 , puis en donner
l'arrondi à l'unité.
La poubelle cylindrique, posée dans la sphère, s’appuie sur les
parois de cette dernière, le long de ses deux bases circulaires de diamètres
respectifs [AB] et [DC], AB = DC = 2r.
De plus, la poubelle cylindrique possède la même symétrie
centrale de centre O que la sphère de centre O et de rayon 6 dm.
La figure ci-dessous montre, en exemple, deux positions possibles de la poubelle dans la sphère : (ABCD) et (A’B’C’D’).
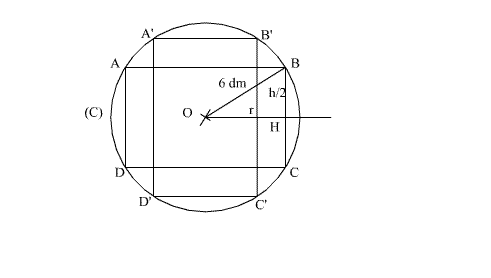
Considérons la position quelconque (ABCD) de la poubelle.
Soit [OH] la perpendiculaire menée de O à [BC] qui rencontre ce
dernier au point H.
Le triangle (OHB) étant un triangle rectangle en H, le théorème
de Pythagore donne :
![]()
On sait que :

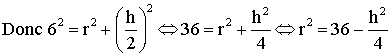
et finalement on a :
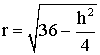
2)
a-
le volume V(h) de la poubelle est :
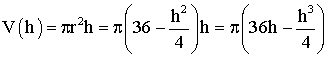
b-
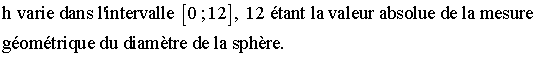
Calculons la dérivée de V(h) par rapport à la variable h ;
on a :
![]()
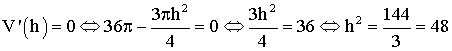
![]()
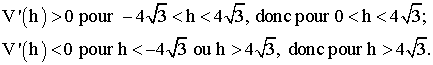
Conclusion :
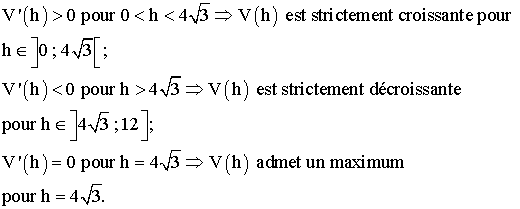
3)
a-
D’après la conclusion de la question 2) b-, on a :
![]()
b-
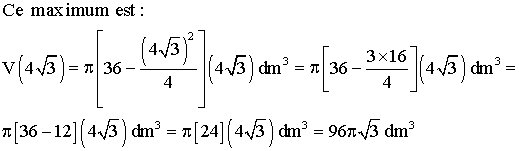
On a :
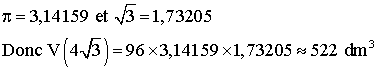
page 1 page 2 page 4 page 5 page 6