L'EXERCICE
POUR LA SECONDE ET LA PREMIERE S
(page 6)
les thèmes abordés dans cette page
existence des racines
d'une équation
(2de)
étude d'une fonction
dont l'expression comporte
la valeur absolue d'un terme
(1ère S)
projections sur un plan
et lieux géométriques
(1ère S)
existence des racines
d'une équation
(groupe ciblé : seconde)
On
donne la fonction g définie par :
![]()
En étudiant la continuité, la monotonie et les variations de g respectivement dans les intervalles suivants :
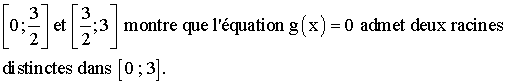
Rappel
d’une propriété fondamentale : si une fonction
f est définie et continue sur un intervalle [a ; b], strictement
croissante (ou strictement décroissante) sur l’intervalle ]a ; b[ et si
f(a).f(b) est strictement négatif, alors il existe un réel x0 et
un seul appartenant à [a ; b], tel que f(x0) est nulle ;
autrement dit l’équation f(x) = 0 admet une racine et une seule.
Géométriquement, si dans un repère, C est la courbe représentative
de f définie et continue sur l’intervalle [a ; b] et si de plus f vérifie
la propriété précitée, alors C coupe l’axe des abscisses en un point et
un seul appartenant à [a ; b].
Solution
![]()
![]()
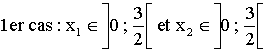
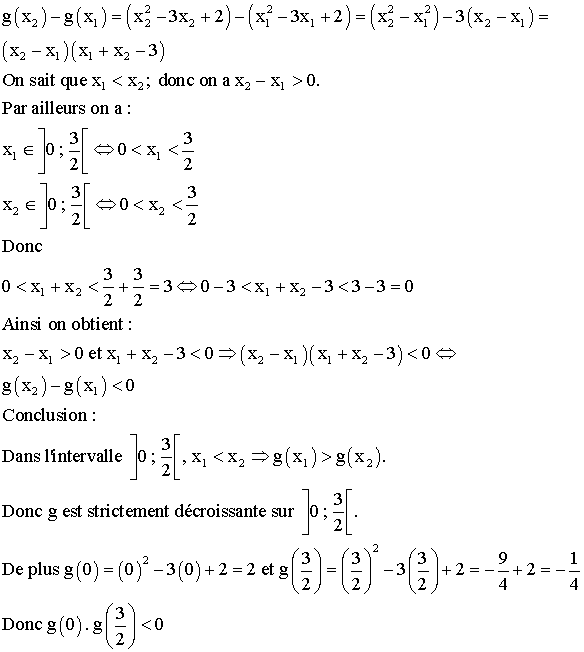
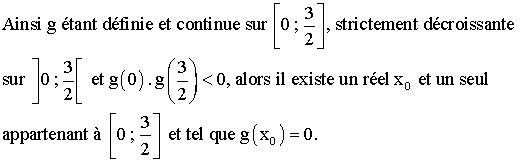
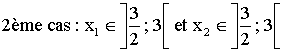

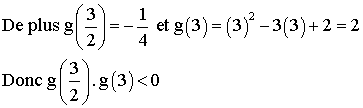
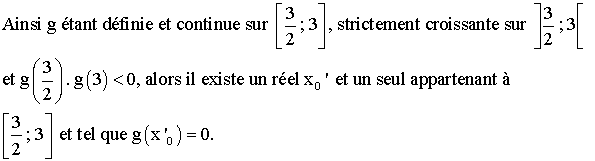
Conclusion
générale :

étude d'une fonction
dont l'expression comporte
la valeur absolue d'un terme
(groupe ciblé : première S)
On
donne la fonction f définie par :
![]()
Quel
est le domaine de définition de f ?
Étudie la continuité et les variations de f. Construis sa courbe représentative (D).

(On
prendra un repère orthonormal)
Solution
f est
définie sur R ; donc dom(f) = R.
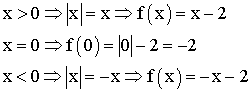

Conclusion :
![]()
Calculons
la dérivée de f. On a :
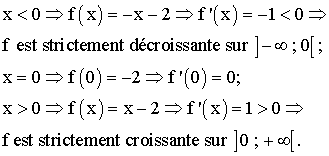
![]()
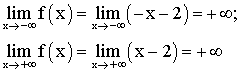
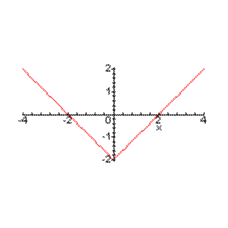
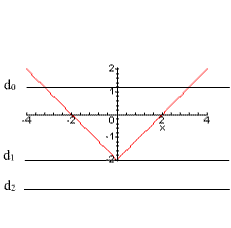
D’où
le tableau des variations de f suivi de sa représentation graphique (D)
dans un repère orthonormal :

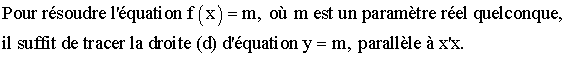

projections sur un plan
et lieux géométriques
(groupe ciblé : première S)
On considère deux axes orthogonaux X’X et Y’Y, leur perpendiculaire commune [AB], A appartenant à X’X et B appartenant à Y’Y.
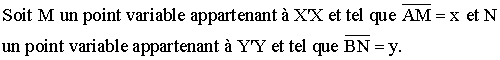
Soit
I le milieu de [MN]. On désigne par I’ et N’ les projetés orthogonaux
respectifs de I et de N sur le plan P déterminé par X’X et u’u, la parallèle
à Y’Y menée de A.
a-
Calcule MN en fonction de a, x et y.
![]()
c- Trouve l’ensemble des points I’ et déduire celui de I dans chacun des
cas suivants :
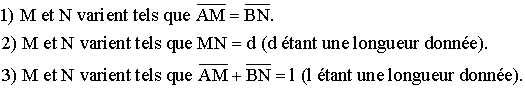
Solution
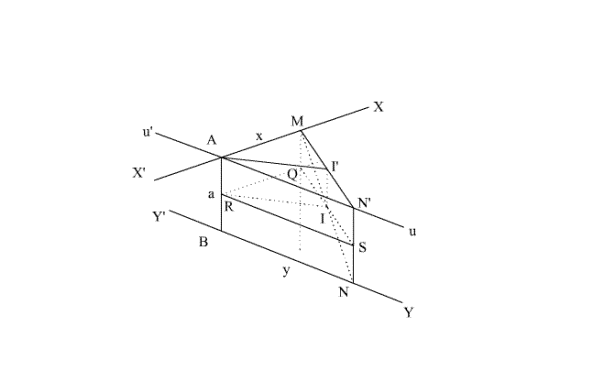
a-
(AB)
étant la perpendiculaire commune à X’X et Y’Y, est donc orthogonale au
plan P.
(AB)
et (NN’) étant orthogonales au plan P, sont parallèles.
Par construction, u’u est parallèle à Y’Y ; donc (AN’) est parallèle
à (BN).
Ainsi le quadrilatère (ABNN’) ayant ses côtés deux à deux parallèles est
un parallélogramme et on a AB = NN’ = a et N’A = BN = y
Remplaçons
dans l’égalité (1) MN’2 et NN’2 par leurs égales
x2 + y2 et a2 ; on obtient donc :
![]()
b-
I’
étant le projeté orthogonal de I sur P, alors (I’I) est orthogonale à P,
donc à toute droite de P et en particulier à (MN’).
Ainsi dans le triangle rectangle (MNN’), (I’I) et (NN’) sont parallèles ;
de plus, comme I est milieu de [MN], alors I’ est milieu de [MN’].
Donc dans ce triangle, [I’I] joignant les milieux des deux côtés [MN] et [MN’]
a pour mesure géométrique la moitié de celle du troisième côté [NN’].

c-
![]()
P’
est donc parallèle à P.
![]()
(AB)
étant orthogonale à P, alors elle est orthogonale à P’. Ainsi le plan P’
orthogonal à (AB) fixe et passant par son milieu R, est fixe. P’ est donc le
plan médiateur du segment fixe [AB].
Soient S et Q ses intersections respectives avec (N’N) et la droite
orthogonale à P menée de M.
1)
![]()
Ainsi
le triangle rectangle (AMN’) est également isocèle.
La médiane (AI’) est également bissectrice de l’angle au sommet fixe A et
de côtés fixes [Au et [AX.
Donc l’ensemble des points I’ inclus dans le plan fixe P est la droite (AI’)
support de cette bissectrice fixe.
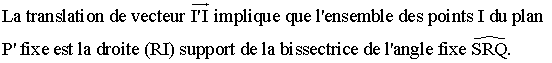
2)
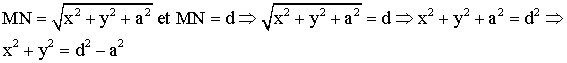
Notons
que d doit être supérieure à a.
Dans le triangle rectangle (AMN’), la mesure géométrique de la médiane relative à l’hypoténuse [MN’] est égale à la moitié de celle de cette dernière.
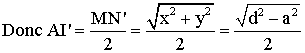
Ainsi
dans le plan fixe P,

3)
Dans la plan fixe P, on a :

Considérons le repère (X’X ; u’u) qu’on oriente.
Dans ce repère projetons orthogonalement I’ sur X’X et sur u’u ;
comme I’ est milieu de [MN’], on a :
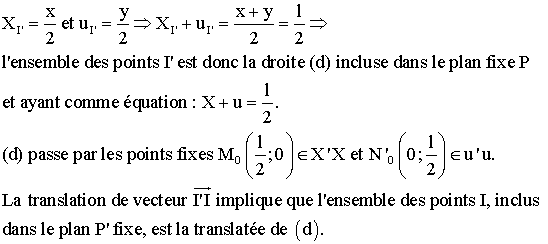
page 1 page 2 page 3 page 4 page 5
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)