L'EXRCICE
POUR
LE COLLEGE
(page 4)
les
thèmes abordés dans cette page
symétrie axiale et centre du cercle
inscrit
dans un triangle
(4ème)
propriétés des puissances de nombres
(4ème)
angle
inscrit et lieu géométrique
(3ème)
résolution
algébrique de problèmes
(3ème)
symétries
axiales et centre du cercle inscrit
dans un triangle
(groupe
ciblé : quatrième)
Soit (ABC) le triangle dont les mesures géométriques
des côtés sont : AB = AC = 5 cm et BC = 3,5 cm.
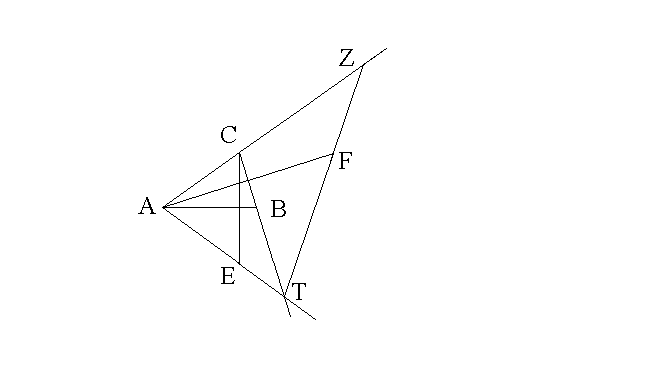
Soit E le symétrique de C par rapport à la droite (AB). L’intersection des
droites (AE) et (BC) est T.
![]()
2) Soit F le symétrique de A par rapport à la droite (BC). Quelle est la nature du triangle (ATF) ?
![]()
3) Les droites (AC) et (TF) se coupent en Z.
![]()
Solution
Rappel du cours de sixième :
la symétrie axiale conserve les mesures géométriques des
segments ainsi que les angles.
L’image de (AB) par S est (AB) ; celle de (AC) est (AE).

ceci car la symétrie
axiale conserve les angles.
2)
Posons s la symétrie axiale d’axe (BC).
s(A) = F ; T appartient à (BC), donc s(T) =
T.
s(A) = F et s(T) = T implique que s([AT]) = [FT] ; et ainsi AT = FT et le triangle (ATF) est isocèle ;
ceci car la symétrie axiale conserve les mesures géométriques des segments.
L’image de (TC) par s est (TC) ; celle de (TA) est (TF).

ceci car la symétrie axiale conserve les angles.
3) Dans le triangle (AZT), on a :
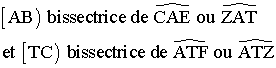
Donc
B est centre du cercle inscrit dans le triangle (AZT) ou encore l’intersection des deux
bissectrices [AB) et [TC).

Pythagore
(groupe ciblé : quatrième)
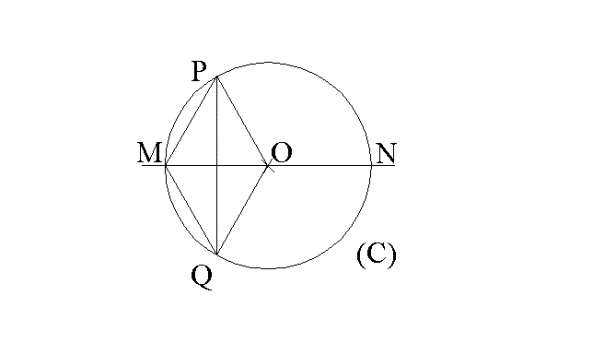
On te donne un cercle C de diamètre [MN] et
de centre O tel que
MN = 8 cm. La médiatrice du segment [MO] coupe C en P et Q.
1) Démontre que MP = 4 cm et que le triangle (MPQ) est équilatéral.
2) Démontre que le quadrilatère (MPOQ) est un losange.
3) Calcule PN2 . Donne une valeur
approximative de PN à 0,1 cm
près par excès.
Solution
1)
(PQ) étant la médiatrice de [MO], PM = OP = 4 cm ; mais aussi PM = OP = OM et
donc
(MPO) est un triangle équilatéral.
2)
On sait qu’un quadrilatère qui a ses quatre côtés de mesures géométriques
égales est un losange.
Comme PM = OP = QM = QO = 4 cm, alors (MPOQ) est un losange.
3)
Dans le triangle (MPN), l’angle intérieur au sommet P est inscrit dans le cercle C et
intercepte le diamètre [AB] ; donc la mesure de cet angle vaut 90° et ainsi (MPN) est un triangle
rectangle en P.
Dans ce triangle et d’après le théorème de
Pythagore on a :
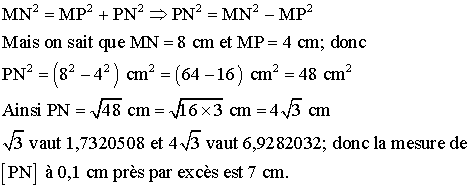
volume d'une
pyramide
(groupe ciblé
: quatrième)
(S , ABCD) est une pyramide dont la base est
un carré (ABCD) de 6 cm de côté.
I est le milieu du segment [AB]. SA = 5 cm et [SI] est la hauteur de la pyramide.
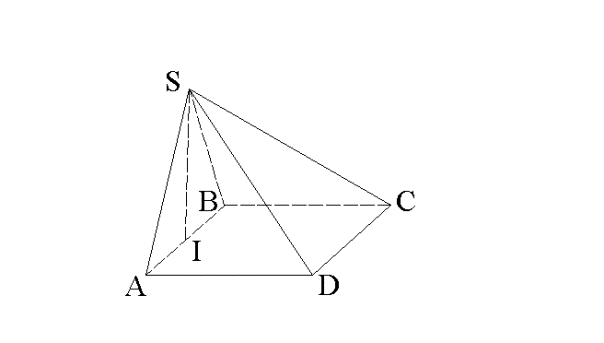
Calcule le volume de cette pyramide.
Solution
I étant le milieu du segment [AB], IA = 3 cm.
Dans le triangle rectangle (SAI), rectangle
en I, le théorème de Pythagore donne :
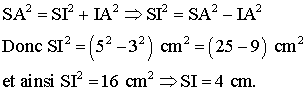
Le volume de cette pyramide est :
![]()
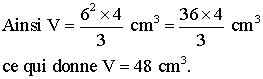
propriétés
des puissances de nombres
(groupe ciblé
: quatrième)
1) Écris sous la forme d’une seule puissance :
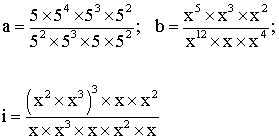
2) Calcule de deux manières différentes :

Rappel du cours :

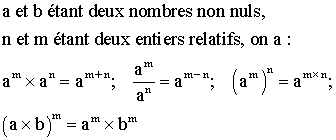
Solution
1)

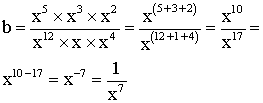

2)

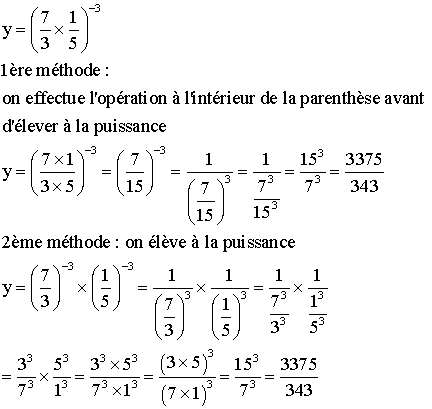
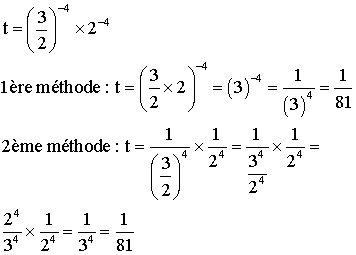
angle
inscrit et lieu géométrique
(groupe ciblé : troisième)

Solution
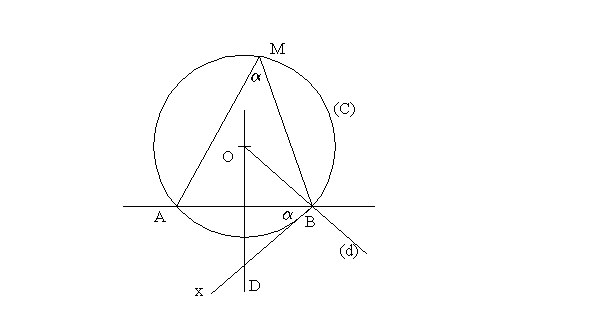
Soit (C) le cercle circonscrit au triangle (AMB).
Soit O son centre.
O appartient à la médiatrice fixe (D) du segment fixe [AB].
Soit [Bx la tangente à ce cercle menée du point B.

![]()
Le rayon [OB] étant perpendiculaire en son
extrémité B à la tangente [Bx, la droite (d), support de [OB]
est ainsi
perpendiculaire à [Bx fixe au point fixe B ; donc (d) est fixe.
Ainsi :

O étant fixe et [OB] étant également
fixe, la mesure du rayon [OB] du cercle (C) est constante.
Donc (C) est fixe.
![]()
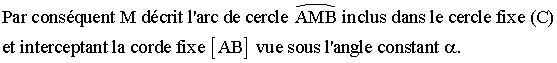
Pour visualiser ce lieu, aller à la page intitulée animation 11.
résolution
algébrique de problèmes
(groupe
ciblé : troisième)
Partie 1
1)
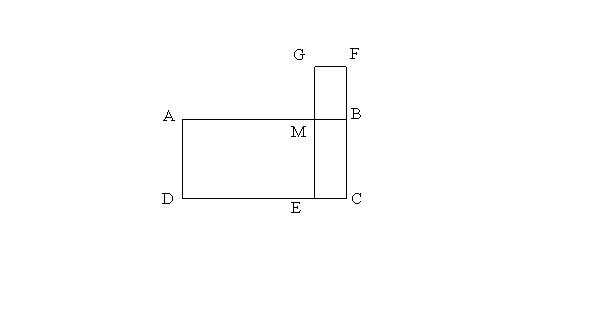
Construire un rectangle (ABCD) tel que :
AB = 6 cm et BC = 3 cm.
Placer un point M sur le coté [AB] distinct de A et de B tel que AM = x cm.
Construire le rectangle (AMED) puis le rectangle (MBFG) extérieur à (ABCD) et
tel que BF = 2 cm.
2)
Exprimer en fonction de x le périmètre p1 du rectangle (AMED) et le
périmètre p2
du rectangle (MBFG).
Pour quelle valeur de x a-t-on p1 = p2 ?
3)
Exprimer en fonction de x l'aire A1 du rectangle (AMED) et l'aire A2
du rectangle (MBFG).
Pour quelle valeur de x a-t-on A1 = A2
?
Solution
1)
La construction des rectangle (ABCD), (AMED) et (MBFG) est
facile ; je te laisse le soin de le faire.
2)
On a AM = x.
![]()
Les dimensions du rectangle (AMED) sont AM = x et
EM = AD = 3 cm.

Les dimensions du rectangle (MBFG) sont MB =
AB – AM =
6 – x
et BF
= 2 cm.
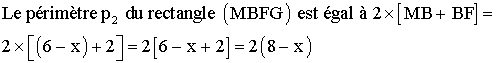

3)
![]()
![]()

Partie 2
Un bassin
est alimenté par deux fontaines dont le débit horaire est constant.
Si on laisse couler la première fontaine pendant 4 heures et la seconde pendant
3 heures,
la quantité d'eau recueillie au total est de 55 litres.
Si on
laisse couler la première fontaine pendant 3 heures et la seconde pendant 4
heures,
la quantité
d'eau recueillie au total est de 57 litres.
1)
Calculer le débit horaire de chacune des deux fontaines.
Sachant que ce bassin peut contenir 320 litres, combien faudra-t-il de temps
pour le remplir,
si les deux fontaines coulent ensemble pendant le même temps ?
Solution
1)
![]()
Si
on laisse couler la première fontaine pendant 4 heures, le volume d’eau
obtenu est de V1 donné par la relation :
![]()
Si on laisse couler la seconde pendant 3 heures, le volume d’eau obtenu est de
V2 donné par la relation :
![]()
On sait que V1 + V2 = 55 l
![]()
Si
on laisse couler la première fontaine pendant 3 heures, le volume d’eau
obtenu est de V’1 donné
par la relation :
![]()
Si on laisse couler la seconde pendant 4 heures, le volume d’eau obtenu est de
V’2 donné par la relation :
![]()
On sait que V’1 + V’2 = 57 l
![]()

A
l’aide de la première équation, calculons Q2 en fonction de Q1 ;
il vient :
![]()
Remplaçons,
dans la seconde équation, Q2 par son égale trouvée ; il vient :

Remplaçons dans une des équations
du système, Q1 par 7 l / h ; il vient :
![]()
2)
Les deux fontaines coulant en même temps,
supposons T en heures, la durée du remplissage
de ce bassin ; on a donc :
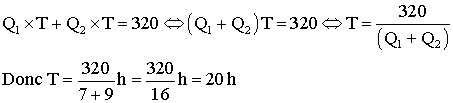
Partie 3
1)
Construire un triangle
isocèle (ABC) de sommet A et tel que :
![]()
2)
![]()
a- Démontrer que les triangles (CBD) et (BDA) sont isocèles.
b- Démontrer que les triangles (BAC) et (CBD) sont semblables.
![]()
3)
![]()
![]()
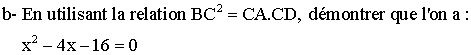

Solution
1)
La construction est facile ; je te laisse le soin de la faire.
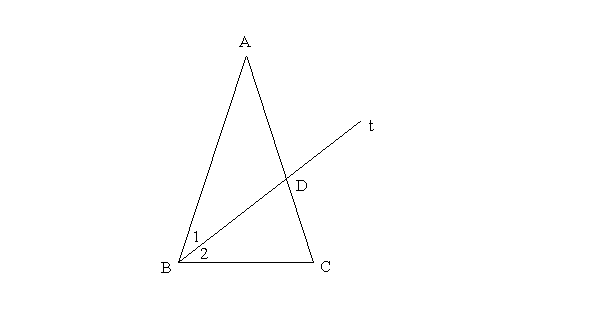
2)
a-
Soit [Bt la bissectrice de l’angle intérieur au sommet B.
Elle coupe [AC] en D.
![]()
On sait que dans un triangle, la somme
des angles intérieurs est égale 180°.
Donc
dans le triangle (CBD) on a :



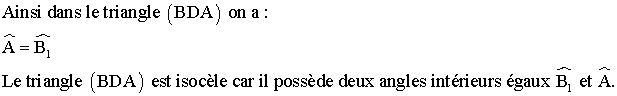
b-

On sait que si deux triangles ont deux angles intérieurs respectivement
égaux, alors ces deux triangles
sont semblables.
Donc (BAC) et (CBD) sont semblables.
Ainsi, on a :
![]()
Ce qui donne :
![]()
3)
a-

b-
On a montré la relation :
![]()
![]()
c-
Notons d’abord que x étant un mesure géométrique
d’un côté d’un triangle, doit être positive.
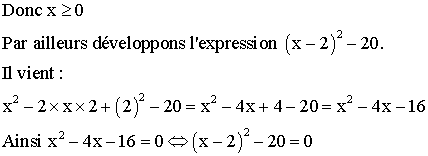
Cette dernière égalité est de la forme :