
L'EXERCICE
POUR
LE COLLEGE
(page 5)
les thèmes abordés dans cette page
application de la notion de cosinus de la mesure d'un
angle aigu
(4ème)
équation
d'une droite et calculs trigonométriques
(3ème)
fonction numérique et résolution d’équations
(3ème)
développement
et factorisation
(3ème)
application de la notion de cosinus de la mesure
d'un angle aigu
(groupe ciblé : quatrième)
1- Rappel
Un triangle dont un de ses angles intérieurs est droit est appelé triangle rectangle.
Le côté opposé à son angle droit est appelé hypoténuse.
L’hypoténuse est le côté qui a la plus grande longueur.

La figure ci-dessus représente un triangle (ABC) rectangle en A.
Son hypoténuse est [BC].
On remarque que la longueur de
l’hypoténuse est plus grande que chacune des
longueurs
des deux autres côtés : [AC] et [AB].
En effet, la longueur d’une oblique est plus grande que celle de la hauteur.
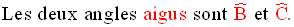

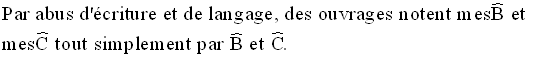


Dans un triangle
rectangle, les cosinus de la mesure d’un angle aigu est le rapport de
la longueur
du côté
de l’angle droit qui lui est adjacent à la longueur de l’hypoténuse.
Plus haut, on avait dit que la longueur de l’hypoténuse est plus grande que chacune des longueurs des deux autres côtés.
Donc,
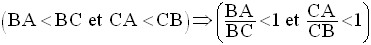
Dans un triangle rectangle, les cosinus de la mesure d’un angle aigu est strictement inférieur à 1.
Cette propriété est importante :
dans un calcul, si l’on rencontre une valeur pour le cosinus supérieure à
1,
alors cela signifie que l’on a fait une erreur quelque part.
2- Formules
On considère la figure du paragraphe 1.

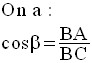
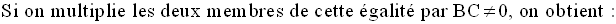
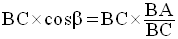

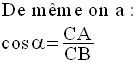

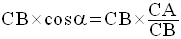

Conclusion
Dans un triangle
rectangle, la longueur de chacun des côtés de l’angle droit est égale
au produit
de la longueur
de l’hypoténuse par le cosinus de la mesure de l’angle aigu qui lui est
adjacent.
3- Applications
Application 1
On donne le triangle rectangle (ABC) suivant :

On donne AC = 3cm, BC = 5cm et AB = 4cm.
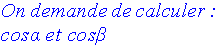
Solution
On a par définition :
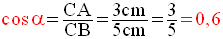
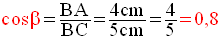
On remarque bien que ces deux valeurs trouvées sont strictement inférieures à 1.
Application 2
On donne le triangle rectangle isocèle (ABC) suivant :

En utilisant le
théorème de Pythagore et la définition du cosinus de la mesure d’un angle aigu
dans un triangle rectangle, on te demande de calculer :
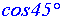
Solution
D’après la figure, on a :
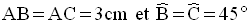
Par définition, on a également :
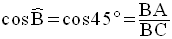
BA est donnée et vaut 3cm.
Il faut donc calculer BC, la longueur de l’hypoténuse. Pour cela on doit appliquer le théorème de Pythagore.
Rappel :
dans un triangle rectangle, le
carré de la longueur de l’hypoténuse est égal à la somme
des carrés
des longueurs des deux autres côtés.
Ainsi, on a :
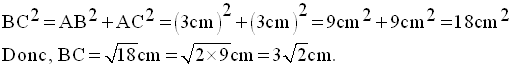
Finalement, on obtient :
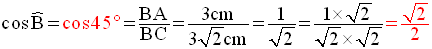

Remarque :
on aurait pu utiliser la définition du cosinus de la mesure de l’angle aigu en
C ;
le résultat est le même.
Application 3
On donne le triangle demi équilatéral (ABC) suivant :

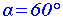
En utilisant le
théorème de Pythagore, une propriété du triangle demi équilatéral et la
définition
du cosinus
de la mesure d’un angle aigu dans un triangle rectangle, on te demande de
calculer :
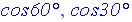
Solution
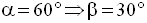
Par définition, on a :
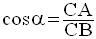
CB peut être calculée en fonction
de CA. Pour trouver cette valeur de CB, on doit appliquer une propriété
du triangle demi équilatéral : la longueur du côté opposé à l’angle aigu
dont la mesure est 30° est égale
à la
moitié de la longueur de l’hypoténuse.
Ainsi,
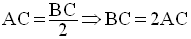
Finalement, on obtient :
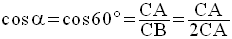
En simplifiant par CA différente de zéro, on obtient :
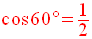

Par définition, on a :
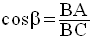
On a démontré que :
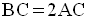
BA peut également être calculée
en fonction de CA.
Pour trouver cette valeur de BA, on doit appliquer le théorème de Pythagore.
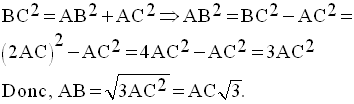
Finalement, on obtient :
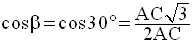
En simplifiant par AC différente de zéro, on obtient :
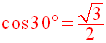

Application 4
Une échelle s’appuie sur un mur vertical.
Le pied de cette échelle se trouve à 0,75mètre de celui du mur.
Dans cette position, l’échelle fait avec le sol supposé horizontal un angle de 80°.
On donne :
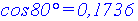
On te demande de calculer la longueur de cette échelle.
Solution
On a la figure suivante :

BC est la longueur de l’échelle à calculer.
On sait que
dans un triangle rectangle, la
longueur de chacun des côtés de l’angle droit est égale au
produit de la longueur de l’hypoténuse par le cosinus de la mesure de l’angle
aigu qui lui est adjacent.
L’angle aigu adjacent à [AC] est l’angle au sommet C. Il mesure 80°.
On a donc :
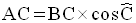
De cette formule, on déduit que :
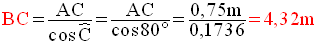
Application 5
Un géomètre,
situé à une distance horizontale de 15m d’un arbre quasiment vertical, vise son
sommet
avec un instrument optique qui lui permet de trouver l’angle que fait la ligne
de visée avec un plan
horizontal (H) passant par son oeil.
Il trouve 65°.
On suppose le sol horizontal.
(H) rencontre l’arbre à 1,25m du sol.
On te demande de calculer la hauteur de cet arbre.
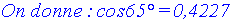
Solution
On a la figure suivante :
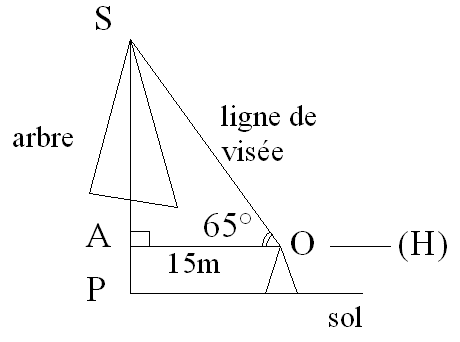
L’œil de l’opérateur est O.
AP = 1,25m
On calcule d’abord SO.
Connaissant AO et SO, et sachant
que l’arbre est vertical, donc l’angle en A formé avec (AS) et (AO) droit,
le théorème de Pythagore appliqué au triangle rectangle (ASO) permet de calculer
AS.
La hauteur de l’arbre sera donc AS + AP.
Calcul de SO
On sait que
dans un triangle rectangle, la
longueur de chacun des côtés de l’angle droit est égale au produit
de la longueur de l’hypoténuse par le cosinus de la mesure de l’angle aigu qui
lui est adjacent.
L’angle aigu adjacent à [AO] est l’angle au sommet O. Il mesure 65°.
On a donc :
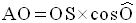
De cette formule, on déduit que :

Le théorème de Pythagore appliqué au triangle (ASO) rectangle en A donne :
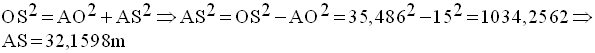
La hauteur de l’arbre sera donc :
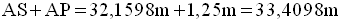
Cette hauteur, arrondie, est donc égale à 33,41m.
équation
d'une droite et calculs trigonométriques
(groupe
ciblé : troisième)
Partie 1
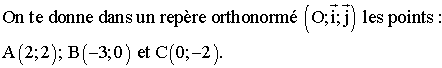
L’unité de longueur prise sur les axes est le
centimètre.
1-
Trouve l’équation de la hauteur du triangle (ABC) abaissée de
A.
Soit H le pieds de cette hauteur.
Trouve les cordonnées de H et calcule AH.
2-
Calcule l’aire du triangle (ABC)
3-
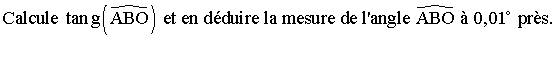
4-
![]()
5-
En t’inspirant des questions 3 et 4, calcule les mesures de l’angle au
sommet C du triangle (ABC) et
en déduire celle de l’angle au sommet A.
Solution
1-
L’équation de la hauteur du triangle (ABC) abaissée de A est de la forme :
y = ax + b
Elle passe par le point A ; donc les coordonnées de A doivent la vérifier et on a donc :
yA = axA + b ou encore 2 = 2a + b
Trouvons l’équation de (BC).
Elle est de la forme y = mx + n et passe par B et C ; donc les coordonnées
de B et de C devront vérifier cette équation et on a donc :
yB = mxB + n et yC = mxC + n ou
encore 0 = -3m + n et –2 = 0m + n
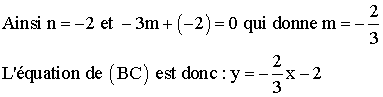
Par ailleurs la hauteur abaissée de A devant être
perpendiculaire à (BC), le produit des coefficients
directeurs des équations
de ces deux droites devra être égal à –1 ; donc on a :
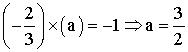

H appartient à la fois à (BC) et à cette
hauteur ; ses coordonnées devront vérifier simultanément
les deux équations
et on a :
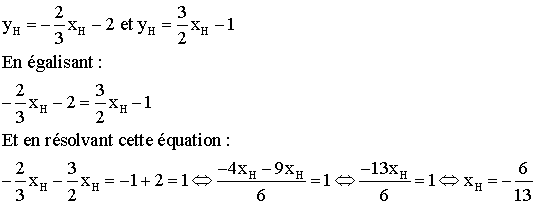
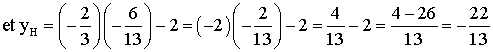
Le théorème de Pythagore donne :
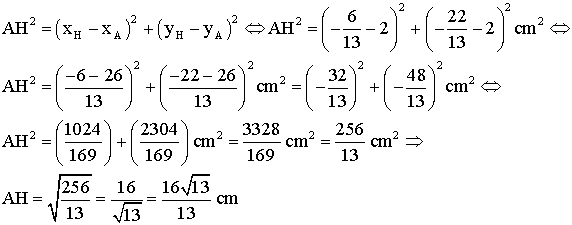
2-
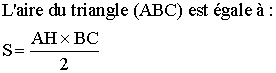
On a calculé AH ; il nous reste à calculer BC.
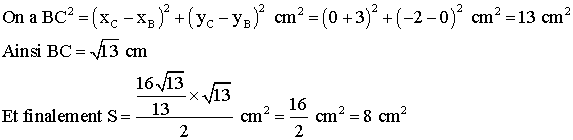
3-
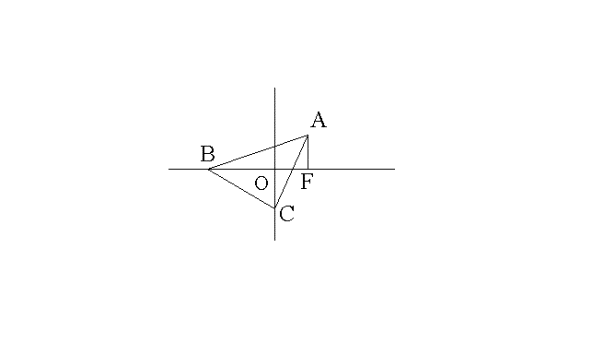
Soit F la projection orthogonale de A sur l’axe des abscisses.
Dans le triangle (ABF) rectangle en F, on a :
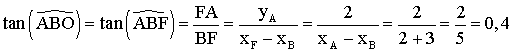
![]()
4-
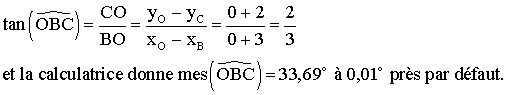
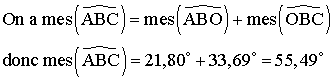
5-
Soit K la projection orthogonale de A sur
l’axe des ordonnées.
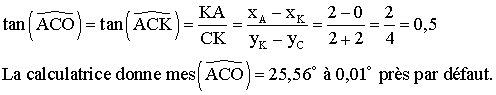
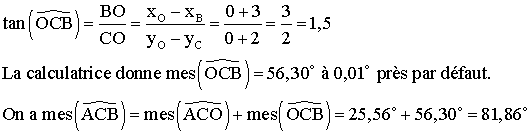
On sait que dans un triangle, la somme des
mesures des trois angles intérieurs est égale à 180° .
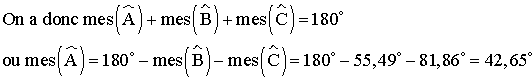
Partie 2
On donne la mesure a d’un angle aigu dont le
sinus vaut 0,355.
Calcule cos(a) et tan(a).
solution
Rappel de cours


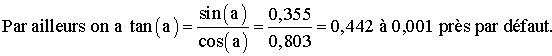
fonction numérique et résolution d’équations
(groupe
ciblé : troisième)
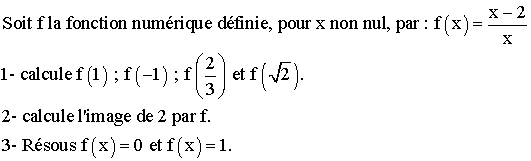
solution
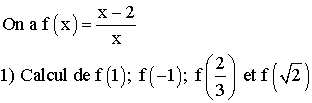
Pour calculer f (x0 ) il suffit de
remplacer dans l’expression de f (x), x par x0 .
Ainsi on a :
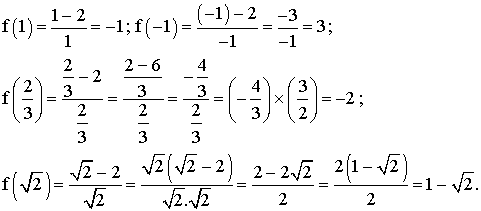
2) Calcul de f (2)
![]()
3) Résolution des équations f (x) = 0 et f (x) =1
Notons d'abord que ces équations n'ont de sens
que pour x appartenant au domaine de définition
de la fonction f,
c'est-à-dire pour les valeurs du dénominateur x différentes de 0.

développement
et factorisation
(groupe
ciblé : troisième)
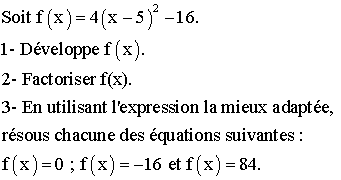
solution
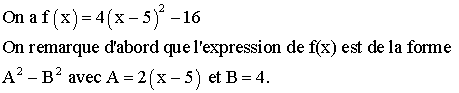
1) Développement de f(x)
![]()
2) Factorisation de l’expression de f(x)
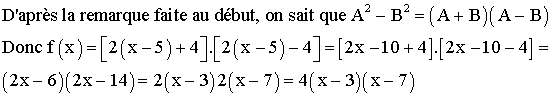
3) Résolution d’équations
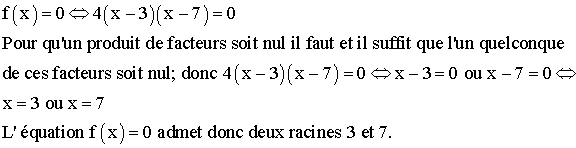
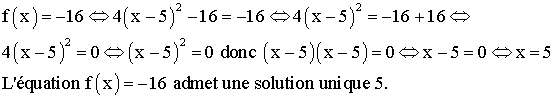
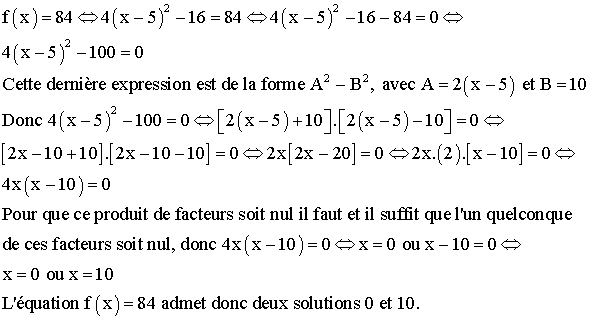
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)