L'EXERCICE POUR LA TERMINALE L
(page 1)

le thème abordé dans cette page

probabilités et suites numériques

probabilités et suites numériques
(groupe ciblé : terminale L)

Première partie

Dans une classe de terminale, la probabilité pour qu'un élève, choisi au hasard, aime la philosophie est 0,5; la probabilité pour qu'il aime l'histoire est 0,7; la probabilité pour qu'il aime simultanément la philosophie et l'histoire est 0,3.

Calcule les probabilités pour qu'un élève choisi au hasard :
1) aime la philosophie et n'aime pas l'histoire;
2) aime la philosophie ou l'histoire;
3) n'aime ni la philosophie ni l'histoire. 

Deuxième partie

e est la base des logarithmes népériens [ln (e) = 1].

Soit la suite (u_n ) à termes strictement positifs de terme initial u₀ = 1 et telle que pour tout entier naturel n,   

a- Calcule u₁ ,  u₂ ,  u₃ .

b- Pour tout entier naturel n, on pose w_n = ln (u_n ). Exprime  w_{n + 1} en fonction de w_n .

c- Soit la suite (v_n ) de terme général, v_n = w_n - 4; donne sa nature ainsi que les élémentsqui la caractérisent.
Exprime (v_n ) en fonction de n et donne sa limite lorsque n tend vers l'infini.

d- En déduis la limite de (w_n ) lorsque n tend vers l'infini puis, après avoir exprimé u_n en fonction w_n , calcule la limite de u_n lorsque n tend vers l'infini.

retour au début de la page

Solutions

Première partie

Identifions les 4 évènements élémentaires :
E₁ : " l'élève aime la philosophie et l'histoire";
E₂ : " l'élève aime la philosophie et n'aime pas l'histoire";
E₃ : " l'élève n'aime pas la philosophie et aime l'histoire";
E₄ : " l'élève n'aime ni la philosophie ni l'histoire".

Nous avons donc : 

E₁ et E₂ étant incompatibles, nous avons :

Il en est de même pour E₁ et E₃ et on a :  

D'où le système :  

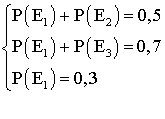
En le résolvant, on trouve :

retour au début de la page

1) La probabilité correspondante est  celle de E₂ , c'est-à-dire 0,2.

2) L'évènement correspondant est   

Mais ces évènements sont deux à deux incompatibles, donc :  

La probabilité cherchée est donc 0,9.

3) La probabilité correspondante est celle de E₄

Nous avons :  

Donc  

et ainsi, la probabilité demandée est 0,1.  

retour au début de la page

Deuxième partie

a- Calculons u₁ ,  u₂ ,  u₃ .

Nous devons trouver 

b- Pour tout entier naturel n, on pose w_n = ln (u_n ).
Exprimons  w_{n + 1} en fonction de w_n .

Nous avons, pour tout entier naturel n :  

c- Soit la suite (v_n ) de terme général, v_n = w_n - 4; donnons sa nature ainsi que les éléments qui la caractérisent.

Nous avons, pour tout entier naturel n :

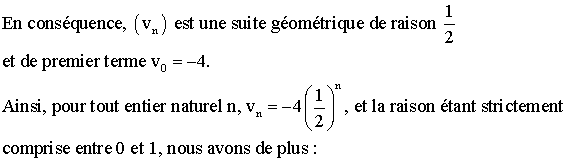
d- Nous savons que, pour tout entier naturel n, v_n = w_n - 4; donc pour n tendant vers l'infini, w_n tendra vers 4 puisque v_n tend vers 0.
Or pour tout entier n,

w_n = ln (u_n ) avec u_n strictement positif; donc nous avons :

D'où pour n tendant vers l'infini, u_n tend vers e⁴ .

retour au début de la page

          page 2          page 3          page 4