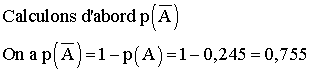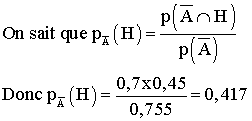L'EXERCICE
POUR
LA TERMINALE L
(page 2)
le thème abordé dans cette page
combinatoire
et probabilités
combinatoire
et probabilités
Une agence de voyages de Paris organise des circuits touristiques
comprenant les sites suivants :
le musée d'Orsay, le musée du Louvre, le musée Grévin, l'Arc de Triomphe, la
tour Eiffel, l'Assemblée nationale.
1. L'agence propose à ses clients un forfait pour la visite de
quatre sites parmi les six cités.
a) Quel est le nombre de choix possibles si on ne tient pas compte
de l'ordre des visites ?
b) Combien de ces choix comprennent à la fois la visite de la tour
Eiffel et celle du musée d'Orsay ?
2. Une étude statistique a permis d'observer que 55% des clients
de l'agence sont des femmes et 45% des hommes. De plus, parmi ces clients, 30%
des hommes et 20% des femmes visitent l'Assemblée nationale.
![]()
a) D'après les informations de l'énoncé, préciser les
probabilités p(F), p(H), pH(A) et pF(A).
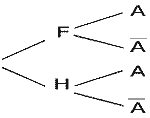
b) Reproduire et compléter l'arbre de probabilité ci-dessous.
En déduire la valeur de p(A).
c) Quelle est la probabilité que le client soit un homme sachant
qu'il ne visite pas l'Assemblée nationale ?
1.
a-
Le nombre de choix possibles, sachant que l’ordre n’intervient pas, est le
nombre des combinaisons de six éléments pris quatre par quatre.
Ainsi on a :
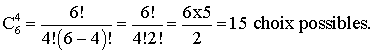
b-
Le nombre de choix, parmi ces 15, comprenant à la fois la visite de la tour
Eiffel et celle du musée d'Orsay est égal à :
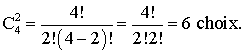
Donc 6 choix comprennent la tour Eiffel et le musée d'Orsay.
2.
a-
p(F) = 0,55; p(H) = 0,45; pH(A) = 0,3; pF(A) = 0,2
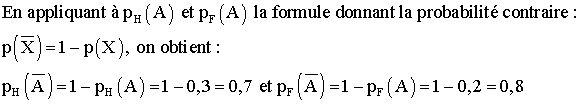
b-
Ainsi on peut, avec toutes ces données, compléter l’arbre qui suit :
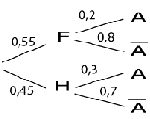
![]()
c-