L'EXERCICE
POUR
LA TERMINALE L
(page 4)
les thèmes abordés dans cette page
Dans un jeu de 52 cartes, quelle est la probabilité de tirer une carte rouge et représentant une figure ?
On suppose l’équiprobabilité. Une figure est un valet ou une dame ou un roi ou un as.
Solution
Soient les deux évènements R : « la carte est rouge » et I : « la carte est image ».
Dans un jeu de 52 cartes, il y a 26 cartes rouges et 16 cartes images.
![]()
![]()
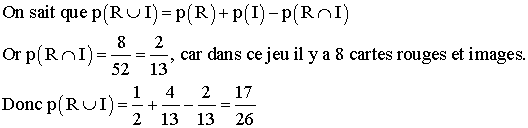
1-


a-
Etudier f et établir son tableau de
variation. Construire sa courbe représentative (C).
b-
Montrer que f(x) = 0 admet dans
l’intervalle de définition de f une unique solution que l’on notera a.
Donner un encadrement d’amplitude 10-3 de a.
2-

b-
Le tableau qui suit représente les variations d’une fonction particulière :
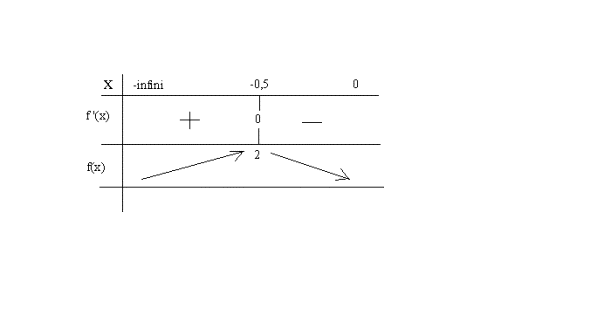
En utilisant les données de ce tableau déterminer les valeurs m et n qui caractérisent cette fonction.
![]()
Montrer que dans l'intervalle [-0,5;-0,01] l'équation f(x) = 0 admet une unique solution.
solution
1-
a-
![]()
De plus f est continue sur son domaine de définition.
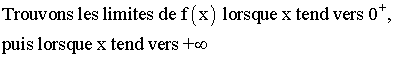
![]()
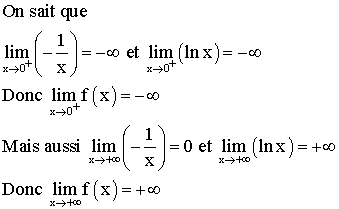


![]()
Par conséquent la fonction f est strictement croissante sur son domaine de définition.
Dressons le tableau de variation de f :
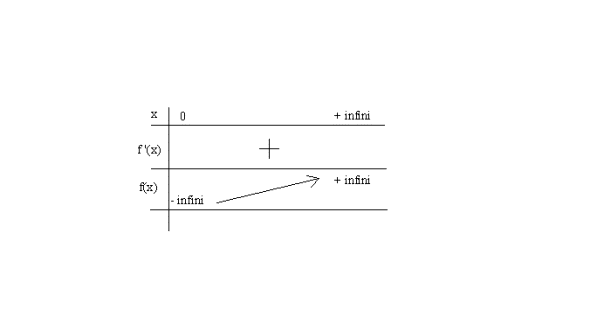
Représentons dans le repère la courbe (C) représentative de f, on obtient :
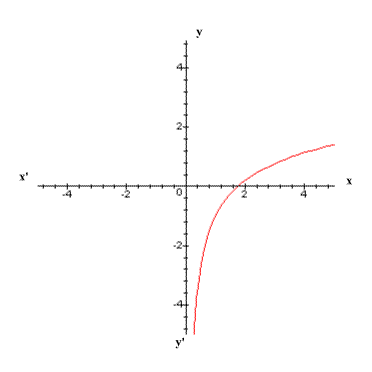
b-
f est continue et strictement croissante sur son domaine de définition ; donc elle l’est également sur l’intervalle [1 ;2].
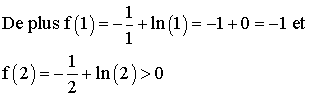
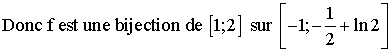
Comme f(1).f(2) < 0, alors il existe un réel a et un seul appartenant à [1 ;2] tel que f(a) = 0.
Donnons un encadrement d’amplitude 10-3 de a.
Nous allons utiliser ici la méthode par « dichotomie » connue également sous le nom de méthode de « Babylone ».
On sait déjà que f(1).f(2) < 0 ; donc 1 < a < 2
On affine l’encadrement de a jusqu’à l’amplitude 10-3
On choisit le milieu de l’intervalle [1 ;2] qui est 1,5 et on considère l’intervalle [1 ;1,5].
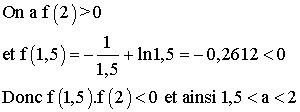
On choisit le milieu de l’intervalle [1,5 ;2] qui est 1,75 et on considère l’intervalle [1,75 ;2].
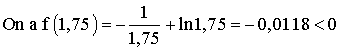
Donc f(1,75).f(2) < 0 et ainsi 1,75 < a < 2
On choisit le milieu de l’intervalle [1,75 ;2] qui est 1,875et on considère l’intervalle [1,875 ;2].
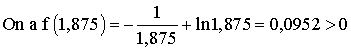
Comme f(1,75) < 0 et f(1,875) > 0, alors f(1,75).f(1,875) < 0
Et on a 1,75 < a < 1,875
Donc on choisit le milieu de l’intervalle [1,75 ;1,875] qui est 1,8125et on considère l’intervalle [1,75 ;1,8125].

Comme f(1,75) < 0 et f(1,8125) > 0, alors f(1,75).f(1,8125) < 0
Et on a 1,75 < a < 1,8125
On choisit le milieu de l’intervalle
[1,75 ;1,8125] qui est 1,78125 et on considère l’intervalle [1,75 ;1,78125].
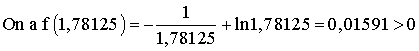
Comme f(1,75) < 0 et f(1,78125) > 0, alors f(1,75).f(1,78125) < 0
Et on a 1,75 < a < 1,78125
On choisit le milieu de l’intervalle
[1,75 ;1,78125] qui est 1,765625 et on considère l’intervalle
[1,75 ;1,765625].
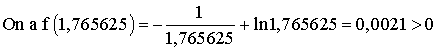
Comme f(1,75) < 0 et f(1,765625) > 0, alors f(1,75).f(1,765625) < 0
Et on a 1,75 < a < 1,765625
On choisit le milieu de l’intervalle [1,75 ;1,765625] qui est 1,7578125et on considère l’intervalle
[1,75 ;1,7578125].
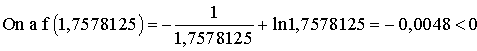
Cette fois-ci f(1,75).f(1,7578125) > 0
Donc il y a lieu de modifier l’extrémité 1,75 de [1,75 ;1,765625] en prenant 1,76 et en calculant f(1,76).
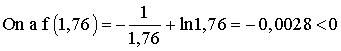
Alors f(1,76).f(1,765625) < 0 et on a 1,76 < a < 1,765625
A partir de là on utilisera la méthode de « balayage » en faisant varier la variable x à partir de 1,76 et par pas de 0 ,001.
Ainsi x balayera les valeurs 1,761 ;
1,762 ;1,763 ;…et ainsi de suite ; on arrêtera dès qu’on
obtient f(x) > 0.
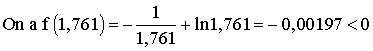
f(1,765625) > 0 et f(1,761) < 0 ; donc 1,761 < a < 1,765625
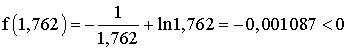
f(1,765625) > 0 et f(1,762) < 0 ;
donc 1,762 < a < 1,765625
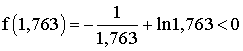
f(1,765625) > 0 et f(1,763) < 0 ; donc 1,763 < a < 1,765625
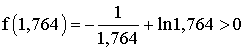
f(1,764) > 0 et f(1,763) < 0 ; donc 1,763 < a < 1,764
Finalement un encadrement d’amplitude 10-3 de a est :
1,763 < a < 1,764
2-

f’ est dérivable sur son domaine de définition et on a :
![]()
b-
D’après le tableau de variation de f, donné, f admet un maximum au point
(-0,5 ; 2). Donc on doit avoir f’(-0,5) = 0 et f(-0,5) = 2
Ceci donne :
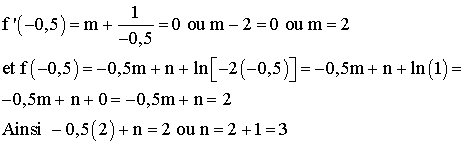
La fonction f est donc :
![]()
![]()
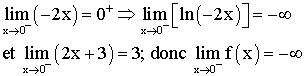
D’après le tableau de variation de f, f est continue
et strictement décroissante sur
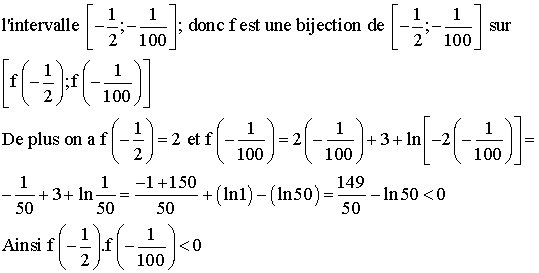
Donc finalement il existe dans l’intervalle [-0,5 ;-0,01] un réel x0 , unique tel que f(x0) = 0.
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)