la multiplication arabe
(groupe ciblé : Sixième)
Tu vas d'abord découvrir cette méthode sur un petit exemple.
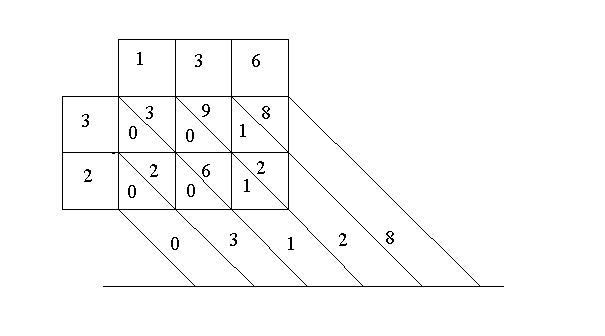
Prends donc la multiplication suivante à effectuer : 136 x 23 .

Trace un tableau à double entrée.
Dans les
cases de la ligne principale, tu disposes les chiffres de l'un des facteurs du
produit, par exemple 136, en allant de gauche à droite et en commençant par
le chiffre de la plus grande unité, ici 1.
Dans les cases de la colonne principale, tu disposes les chiffres de l'autre
facteur, ici 23, en allant du bas vers le haut et en commençant par le
chiffre de la plus grande unité, ici 2.
Tu subdivises les cases du tableau en traçant les diagonales telles que disposées sur la figure ci - dessus, et en les prolongeant. Ainsi, chaque case du tableau est partagée en deux parties dont chacune va recevoir le résultat d'une multiplication.
Chaque case du tableau est à l'intersection
d'une ligne et d'une colonne.
Au
niveau de chacune de ces cases, tu multiplies les chiffres contenus dans les
cases de la ligne et de la colonne principales, par exemple :
3 x 1 = 03 ; 3 x 3 = 09 ; 3 x 6 = 18
2 x 1 = 02 ; 2 x 3 = 06 ; 2 x 6 = 12
Lorsque le résultat de la multiplication est un chiffre, le
chiffre 0 des unités de dizaines y est indiqué :
3 x 1 = 03 ; 3 x 3 = 09 ;
2 x 1 = 02 ; etc.
Tu disposes ensuite les résultats partiels de
ces multiplications dans la case-intersection, de manière que
le chiffre des
dizaines occupe la demi-case inférieur.
Une fois toutes les demi-cases ainsi remplies, tu procèdes à l'addition de
leurs termes diagonaux, en allant
de droite à gauche.
Le résultat de cette addition est indiqué en bas du
tableau .
Cette addition pouvant s'effectuer avec des retenus, ces derniers
sont reportés comme dans
toute addition classique.
Tu obtiens ainsi :
8
9 + 1 + 2 = 12; le chiffre 2 des unités simples est le résultat partiel indiqué
en bas du tableau et le chiffre des dizaines 1 est reporté (retenu) dans la
diagonale qui suit immédiatement
1(retenu) + 3 + 0 + 6 + 1 = 11; le chiffre des unités 1 est le résultat partiel
indiqué en bas du tableau et le
chiffre des dizaines 1 est reporté (retenu) dans la diagonale qui suit
immédiatement
1(retenu) + 0 + 2 + 0 = 3; 3 est le résultat partiel indiqué en bas du
tableau (ici il n'y a pas eu de retenu)
La dernière diagonale comporte une demi-case contenant 0 qui est
indiqué en bas du tableau,
comme dernier résultat partiel de l'addition,
effectuée diagonalement
Le résultat de ta multiplication se lit en bas du tableau, ici 03128
As-tu compris la méthode ?
Invite maintenant trois de tes amis A,
B et C,
en vue de faire l'expérience suivante :
A sera muni d'un chronomètre; il indiquera l'écart de temps entre les deux annonces du
résultat de
la multiplication faites par ton ami B et toi-même
B effectuera la multiplication par la méthode classique d'aujourd'hui
C effectuera la multiplication en se servant d'une calculatrice ou d'un
ordinateur ; son rôle est de
témoigner de la fausseté ou de la justesse de chacun
des résultats qui seront annoncés
Quant à toi, tu effectueras l'opération en utilisant la méthode arabe.
Une fois les dispositions
de la multiplication par les deux méthodes seront effectuées et terminées
par B et toi-même : disposition classique et disposition tableau, le top chrono sera donné, et
surtout noté, au
démarrage du calcul
Le produit proposé est le suivant :
79846759 x 56789
Que constatez-vous à la fin de l'expérience ?
Refaites l'expérience avec le produit :
567894326 x 78965.
triangle et droites parallèles
(groupes ciblés : quatrième et troisième)
Une droite rencontrant deux côtés d'un triangle
et parallèle au troisième côté détermine sur les
deux premiers de segments
dont les longueurs sont dans une proportion.
La méthode qui suit permet
d'éviter des erreurs lors de l'écriture de cette proportion.
Prends par exemple le triangle (ABC) rencontré
par une droite d qui coupe ses côtés [AB] et [AC]
respectivement en M et N et
qui est parallèle au troisième côté [BC] .
En partant du sommet A , écris (ABC) .
Dans le triangle (ANM), à l'angle intérieur en N correspond son égal,
l'angle intérieur en C, dans (ABC).
En dessous de l'écriture (ABC) et en dessous de C, tu places N.
A l'angle intérieur en M correspond son égal,
l'angle intérieur en B.
En dessous de l'écriture (ABC) et en dessous de B, tu places M.
Enfin, comme A est
commun aux deux triangles (ABC) et (ANM), en dessous de A, tu places A.
Ainsi :
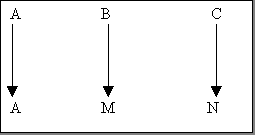
Cette disposition te permet d'écrire la proportion recherchée .
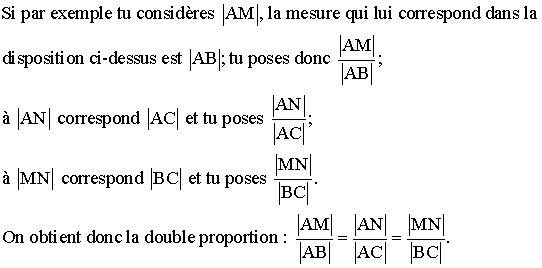
On te donne un triangle (PQR) et une droite (D)
parallèle à [QR] qui rencontre [PQ] et [PR]
respectivement en T et U.
La disposition suivante est-elle juste ?
P Q R
P U T
Si oui, écris la proportion; sinon corrige la et écris la proportion.
Remarque : cette méthode est valable lors de l'application du théorème de Thalès à un triangle.
triangles
homothétiques ou semblables
(groupes ciblés : Seconde et Première)
La méthode d'établissement de la proportion qui
découle de l'homothétie ou de la similitude de deux triangles
est encore
valable.
On te donne deux triangles homothétiques (ABC)
et (A'B'C'); établis la proportion qui lie les mesures de
leurs côtés
sachant que :
![]()
Les triangles (MNP) et (QRS) sont dans une
similitude, avec m = s et p = q.
m, p, s et q sont respectivement les mesures des angles intérieurs de
sommets M et P dans (MNP),
S et Q dans (QRS).
Établis la proportion qui lie les mesures de leurs côtés.
fonctions circulaires
des angles remarquables
(groupe ciblé : Seconde)
Exposons la méthode permettant de trouver les fonctions circulaires des angles remarquables :
0° ; 30° ; 45° ; 60° ; 90°
Remarquons que nous avons classé ces angles par ordre croissant.
On considère la suite
croissante (s0) :
0 ; 1 ; 2 ; 3 ; 4 et la suite croissante (s1) qui en découle :
![]()
En
divisant les éléments de cette dernière suite par 2, on obtient
successivement les sinus de
0° ; 30°
; 45° ; 60° ; 90° .
On obtient ainsi la suite (s2) :
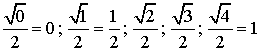
Formons la suite (s3)
qui découle de (s2), en prenant les éléments par ordre
décroissant :
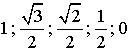
On
obtient ainsi et dans l'ordre les cosinus de 0° ; 30°
; 45° ; 60° ; 90° .
Les tangentes
s'obtiennent en formant la suite des rapports :
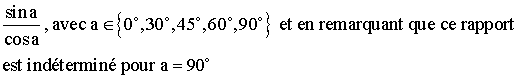
Les
cotangentes s'obtient en passant à l'inverse de la
tangente et en remarquant que, pour a = 0°,
la cotangente est
indéterminée.
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)