IL ETAIT UNE FOIS...LE PASSE DANS LE PRESENT

IL ÉTAIT UNE FOIS ...LE PASSÉ DANS LE PRÉSENT

les thèmes abordés dans cette page

PYTHAGORE et son théorème
(3ème et lycée)

la démonstration par le produit scalaire
(1ères et terminales)

Tabit Ibn Qurra et ses fameuses tranches
(terminales)

équations babyloniennes
(secone et premières)

PYTHAGORE et son théorème
(groupes ciblés : troisième et lycée)

Pythagore fut un mathématicien et un philosophe grec . Il est né en 570 avant Jésus Christ et décédé en 480 avant Jésus Christ .

Il a fondé une école qui , par la suite , porta son nom et donna naissance en Grèce à l'un des plus importants courants philosophiques et mystiques .

Son théorème qui porte son nom a , jusqu'à nos jours , de diverses applications :
topographie , mécanique classique , sciences de l'ingénieur , etc.

Ce théorème s'énonce comme suit : dans un triangle rectangle , le carré de l'hypoténuse est égal à la somme des carrés des deux côtés de l'angle droit .
Il a fait l'objet de plusieurs démonstration , dont une , établie par Léonard de Vinci , ne nécessite aucun calcul . Ce dernier avait énoncé ce théorème de la manière suivante : dans un triangle rectangle , le carré construit sur l'hypoténuse a sa surface égale à celle de la réunion des deux carrés construits sur les deux côtés de
l'angle droit .

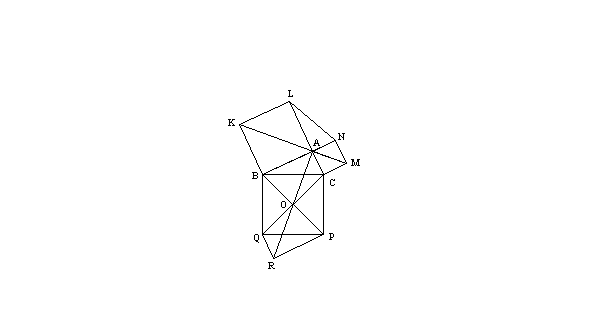
Pour cela , trace sur ta feuille de dessin un triangle rectangle quelconque (ABC) , rectangle en A .
Construis le carré (CBQP) sur l'hypoténuse [BC] , les carrés (ABKL) et (ACMN) respectivement sur les deux côtés [AB] et [AC] de l'angle droit .

retour au début de la page

Les quadrilatères (KLNM) , (KBCM) , (ABQR) , (PRAC) sont " identiques " .
La réunion des deux quadrilatères (KLNM) et (KBCM) a la même surface que la réunion
des deux autres (ABQR) et (PRAC) . La première réunion est composée de deux triangles et des deux carrés construits sur
les côtés [AB] et [AC] ; quant à la seconde , elle est composée
de deux triangles et du carré construit sur l'hypoténuse .

Extrayons un triangle de ces deux réunions ; la surface du polygone (KLANMCB) reste donc égal à celle du polygone (ABQPC) .
De ces deux derniers polygones , extrayons le triangle (ABC) qu'ils ont en commun ; nous en déduisons finalement que la réunion des
deux carrés construits sur les côtés [AB] et [AC] a même surface
que celle du carré construit sur l'hypoténuse .

Ce qui peut s'écrire : |BC|² = |AB|² + |AC|² .

retour au début de la page

la démonstration par le produit scalaire
(groupes ciblés : premières et terminales)

retour au début de la page

Tabit Ibn Qurra et ses fameuses tranches
(groupes ciblés : terminales toutes séries confondues)

A partir du neuvième siècle et jusqu'à 1500 environ , les mathématiques se son épanouies au sein de la civilisation arabe dont le berceau s'étendait de Samarkand à Grenade .

Ils élaborèrent l'algèbre et firent de grandes découvertes en arithmétique , trigonométrie , optique , ...

Ils connaissaient et manipulaient avec aisance les formules donnant la somme des entiers naturels , celle de leurs carrés et cubes .
Par exemple

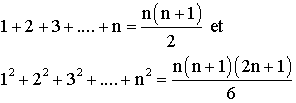
Tabit Ibn Qurra (908 - 946) eut l'idée de découper en tranches verticales la partie tracée entre la parabole (P) d'équation y = x² et la tangente x'Ox à son sommet O , ceci dans l'intervalle [0 ; 1] .

Il effectua la somme des aires des n petites tranches d'épaisseur
1/n et trouva exactement :

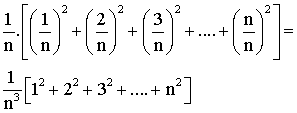
Il mit ensuite cette expression sous la forme
1/6 . (a + 1/n) . (b + 1/n² ) et fit tendre n vers l'infini .
Il déduisit ainsi l'aire exacte comprise entre (P) , l'axe x'Ox et
les deux droites d'équation x = 0 , x = 1 .

A toi de jouer maintenant .
Trouve cette limite et montre la propriété :"
L'aire comprise entre (P) , l'axe des abscisses , les droites
d'équations x = -1 , x = 1 vaut les deux-tiers de l'aire du rectangle
[ -1;1] × [ 0;1] "

retour au début de la page

équations babyloniennes
(groupes ciblés : seconde et premières toutes séries confondues)

En analysant leurs tablettes, nous découvrons que les babyloniens traitaient déjà de problèmes numériques .
Ils les exprimaient en mots et en phrases, sans aucune notation symbolique .

Ils utilisaient un langage géométrique . Par exemple l'inconnue x s'appelait côté; sa puissance deux, c'est-à-dire x² , le carré .

Quand ils faisaient intervenir deux inconnues, ils les nommaient longueur et largeur; leur produit était l'aire .

Ils n'hésitaient pas de soustraire un côté d'une aire défiant ainsi et remarquablement la loi d'homogénéité .
Des phrases telles que : " j'ai soustrait le côté d'un carré de l'aire et le résultat est 3,45 " leur étaient familières .

Dans leurs écrits mathématiques, on retrouve des équations linéaires à une inconnue; des systèmes d'équations à deux inconnues comprenant une équation linéaire et une équation quadratique,
comme :
x ± y = a et xy = b ou encore x ± y = a et x² + y² = b .

Mais également les babyloniens résolvaient des équations quadratiques telles que :
x² - ax = b et x² + ax = b .

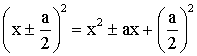
Peux-tu poursuivre pour trouver les solutions à ces équations ?

Les formules donnant ces solutions sont connues depuis Al-Khawarizmi, mathématicien
arabe .