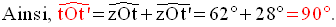
L'EXERCICE
POUR
LE COLLEGE
(page 2)
les thèmes abordés dans cette page
théorème
de Thalès ; maximum d’une fonction numérique
(3ème)
équations du premier degré et application
géométrique
(4ème)
propriétés des figures
géométriques remarquables; calcul d'aires
(5ème)
constructions géométriques : utilisation
de l'équerre, le rapporteur et le compas
(6ème)
théorème
de Thalès ; maximum d’une fonction numérique
(groupe ciblé :
troisième)

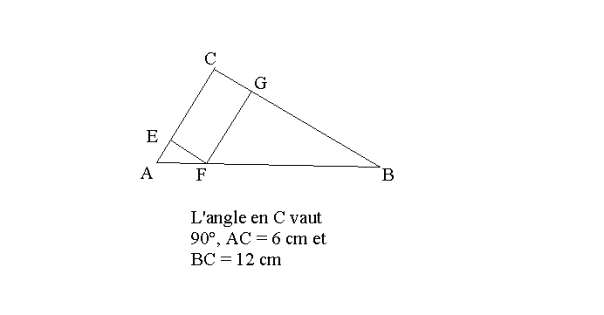
Soit ABC un triangle rectangle en C tel que
AC = 6 cm et
CB = 12 cm.
Soient E un point du segment [AC], F un
point du segment [AB],
G un point du segment [CB], tels que (EFGC) soit un rectangle.
On note AE = x
1-
Pourquoi a-t-on 0 < x < 6 ?
2-
Démontrer que (EF) // (CG).
3-
En utilisant le théorème de Thalès dans le triangle (ACB),
Démontrer que EF = 2x
4-
En déduire l’aire du rectangle (EFGC) en fonction de x.
On notera cette aire A(x).
5-
On suppose dans cette question 5 que EA = 2 cm.
Calculer alors l’aire de (EFGC).
6-
On suppose dans cette question 6 que EA = 0,2 cm.
Calculer alors l’aire de (EFGC).
7-
Quelle doit être la position du point E pour que l'aire du rectangle (EFGC) soit maximale ?
Solution
1-
E se déplace
tout en restant élément du segment [AC]. Il décrit ce segment en allant de A
(x = 0) à
C (x = 6) ; donc :
![]()
Si on écarte
le cas où le rectangle se réduit à un segment (E en A) et le cas où il se réduit
à un
point (E en C), alors 0 <
x < 6.
2-
On sait
que dans un rectangle les côtés opposés sont parallèles.
Or le
quadrilatère (EFGC) étant un rectangle, ses côtés opposés sont parallèles
et ont des mesures égales.
Donc (EF) // (GC) ou (EF) // (BC).
3-
On sait
que dans un triangle, une droite parallèle à un des côtés et rencontrant les
deux autres côtés,
partage ces derniers en des segments dont les mesures sont
respectivement proportionnelles
(théorème
de Thalès)
Or dans le triangle (ABC), on a (EF) // (BC) ; donc :
![]()
On sait que BC = 12 cm, AC = 6 cm et AE = x.
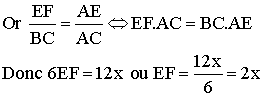
4-
On sait
que l’aire du rectangle (EFGC) est :
EF.EC = (2x).EC
Or EC = AC – AE = 6 – x
Donc A(x) = 2x(6 - x)
5-
A(2) = ?
Il suffit
de remplacer dans A(x) = 2x(6 - x), x par 2 et on obtient :
A(2) = 4(6 - 2) cm2 = 16 cm2
6-
A(0,2) = ?
Il suffit
de remplacer dans A(x) = 2x(6 - x), x par 0,2 et on obtient :
A(0,2) =
2.(0,2)(6 – 0,2) = 0,4(5,8) cm2 = 2,32 cm2
7-
On sait
que deux nombres variant tels que leur somme reste
constante, leur produit atteint
son maximum lorsqu’ils deviennent égaux.
Or :
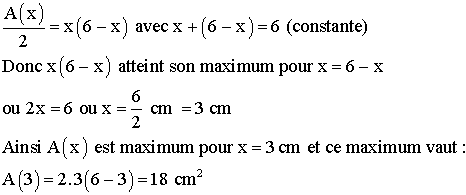
Conclusion :
L'aire de ce rectangle est maximum lorsque le point E se confond
avec le milieu du côté [AC].
équations du premier degré et application
géométrique
(groupe ciblé : quatrième)
Partie 1
On te donne la figure suivante : (ABCD) est un carré dont la mesure commune de ses côtés est x cm.
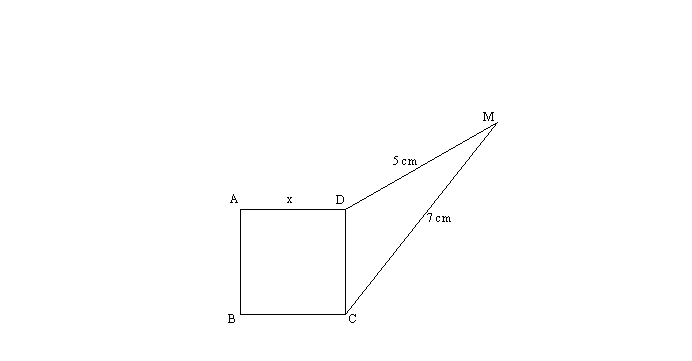
(CDM) est un triangle dont les côtés [DM] et [CM] ont respectivement pour mesures 5 cm et 7 cm.
Calculer l'aire du carré sachant que son périmètre est égal à celui du triangle.
Partie 2
Ta maman a envoyé ton frère aîné acheter du
jus d'ananas à l'épicerie d'à côté.
Il prend un paquet de six bouteilles et se présente à la caisse.
La caissière lui précise alors qu'il lui manque 0,19 €.
Il revient au rayon et pose une bouteille, puis
se présente de nouveau à la caisse et paye.
La caissière lui rend alors 0,95 €.
Quel est le prix d'une bouteille de jus ?
Combien d'argent avait ton frère avant l'achat ?
Solution
Partie 1
Pour
pouvoir calculer l’aire du carré, il faudra calculer d’abord la mesure
commune des ses côtés
qui est x.
Dans ce cas, le périmètre du carré est 4x.
Celui du triangle est x + 5 +7 = x + 12.
On
sait que ces deux périmètres sont égaux ; donc :

L’aire du carré est donc x2 = 42 cm2 ou encore 16 cm2 .
Partie 2
Posons
y le prix en euros d’une bouteille.
Au premier passage de mon frère à la caisse, la caissière lui indique qu’il
lui manque 0,19 €.
Donc
la somme d’argent qu’il avait est 6y – 0,19
Au
second passage, il n’avait plus que 5 bouteille et la caissière lui rend
0,95 € ;
donc la somme d’argent qu’il avait est également :
5y
+ 0,95
En égalisant ces deux expressions et en résolvant l’équation dont l’inconnue est y, on obtient :
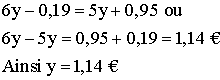
Mon frère avait donc avant l'achat :
(5 x 1,14) + 0,95 € ou 6,65 €
propriétés des figures
géométriques remarquables; calcul d'aires
(groupe ciblé :
cinquième)
Partie 1
(ABC) est un triangle
rectangle et isocèle dont l'angle au sommet B est droit.
M est un point du plan contenant (ABC) tel que (AM) est parallèle à (BC) et
(MC) est parallèle à (AB).
Démontre que le quadrilatère (ABCM) est un carré.
Partie 2
On donne un cercle quelconque
(C) de centre O.
[MQ] et [NP] sont deux diamètres non perpendiculaires de ce cercle.
Démontre que le quadrilatère (PMNQ) est un rectangle.
Partie 3
Calcule les aires des surfaces coloriées suivantes :
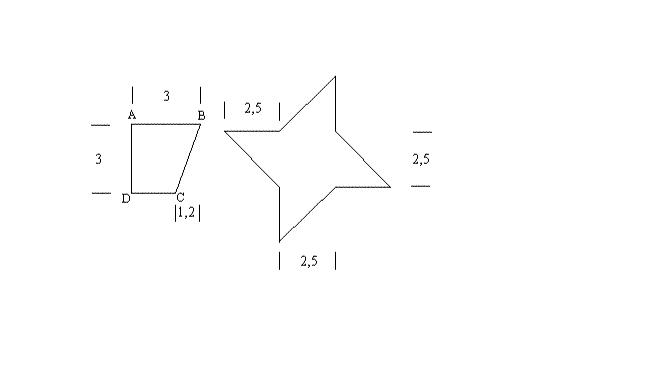
NB : les mesures sont données en centimètre. Les branches de
l'étoile sont des triangles rectangles isocèles.
Solution
Partie 1
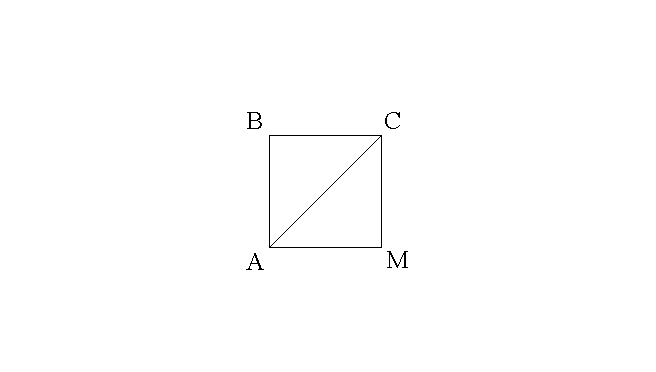
On sait que tout
quadrilatère ayant ses côtés deux à deux opposés et parallèles est un
parallélogramme.
Comme (AM) est parallèle à (BC) et
(MC) est parallèle à (AB), alors (ABCM) est un parallélogramme.
On sait que tout
parallélogramme ayant un de ses angles intérieurs droit est un
rectangle.
Comme l'angle intérieur au sommet B du parallélogramme (ABCM) a pour mesure
90°, alors (ABCM)
est un rectangle.
On sait que tout rectangle
ayant deux côtés adjacents de mesures géométriques égales est un carré.
Comme (ABC) est un triangle rectangle isocèle, donc AB = BC, alors le rectangle
(ABCM) possède
deux côtés adjacents [AB] et [BC] tels que AB = BC et ainsi
(ABCM) est un carré.
Partie 2
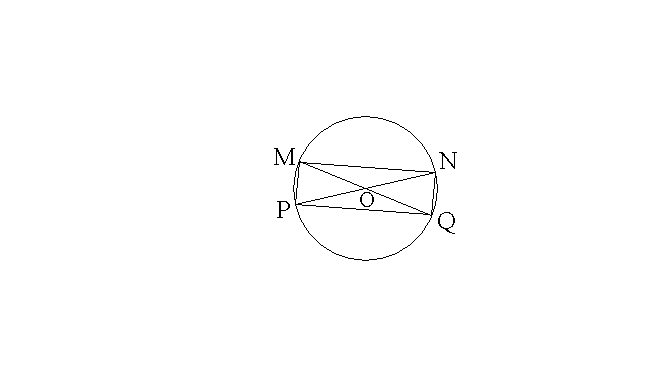
On sait que tout quadrilatère ayant les diagonales se coupant en leur milieu et de mesures géométriques égales est un rectangle.
Comme [MQ] et [NP] sont deux
diamètres d'un même cercle, alors ils se coupent en leur milieu qui est le
centre O et ont la même mesure géométrique.
Alors le quadrilatère (PMNQ) est un rectangle.
Partie 3
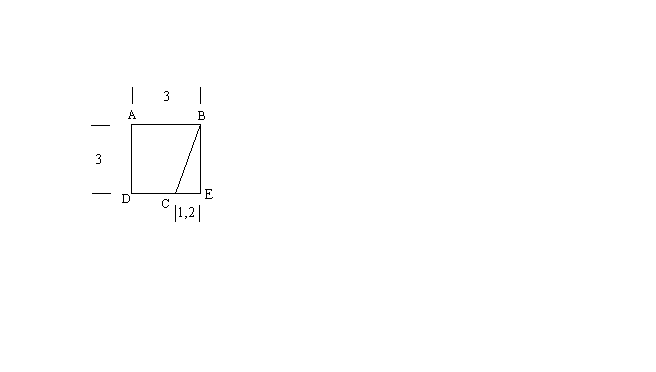
Complétons la figure en prolongeant les droites (DC) et et la
perpendiculaire menée de B à (AB); ces
deux droites se coupent en E.
Si A est l'aire du triangle rectangle (BCE), alors :
![]()
Si B est l'aire du carré (ABED), alors :
![]()
L'aire du trapèze (ABCD) sera donc :
![]()
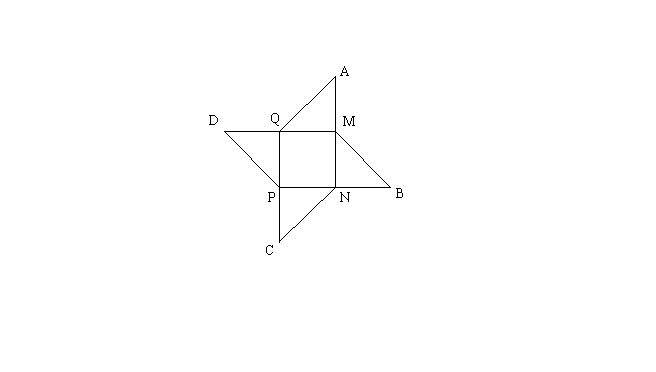
Les
quatre branches de l'étoile sont toutes identique à un triangle rectangle
isocèle.
Donc l'aire totale de ces quatre branches sera égale à l'aire de
l'une d'elle multipliée par 4.
Appelons S cette aire, alors :
![]()
Si S' est l'aire du carré (MNPQ), alors :
![]()
L'aire de l'étoile sera donc :
![]()
constructions
géométriques : utilisation de l'équerre, le rapporteur et le compas
(groupe ciblé : sixième)
J’observe
Une règle est une barre droite généralement graduée en centimètre, jusqu’à 30 cm.
Pour être utilisable, elle doit satisfaire deux conditions :
1-
son bord droit utilisé pour tracer des droites doit être lisse et ne doit
pas comporter
des brisures ou cassures
2- sa graduation doit être parfaitement lisible
Une équerre est un
instrument qui a la forme d’un triangle rectangle. Au moins un de ses bords
formant l’angle droit est gradué en centimètre.
L’équerre sert généralement à tracer une droite perpendiculaire à une droite donnée.
Pour être utilisable, elle doit satisfaire deux conditions :
1- ses trois bords doivent être lisses et ne doivent pas comporter des brisures ou cassures
2- ses graduations doivent être parfaitement lisibles
Un compas est un
instrument composé de deux bras qui s’articulent aisément autour d’un point
qui
se matérialise par un système de vissage.
L’un de ses bras se termine
par une pointe métallique.
L’autre bras se termine par une mine permettant de
tracer des cercles ou des arcs de cercle.
Pour être utilisable, il doit satisfaire trois conditions :
1- ses bras doivent s’articuler facilement, avec un vissage suffisant pour maintenir une ouverture voulue
2- La pointe métallique d’un des bras doit être parfaitement pointue
3- La mine qui termine l’autre bras doit être en parfait état
Il est l’instrument le plus polyvalent ; il sert
à :
- tracer des cercles et arcs de cercle
-
tracer la droite passant par un point donné et perpendiculaire à une
droite donnée,
cette dernière ne contenant pas le point donné
-
tracer la droite passant par un point donné et parallèle à une droite
donnée,
cette dernière ne contenant pas le point donné
- tracer la médiatrice d’un segment donné
- tracer la bissectrice d’un angle donné
Un rapporteur a la
forme d’un demi-cercle. Son bord courbé représente ce demi-cercle et
comporte
deux graduations allant de 0 degré à 180 degrés, dans un sens et dans l’autre.
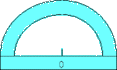
Son bras droit comporte en
son milieu un point repère (O sur la figure) qui, lors de l’utilisation de
cet
instrument, doit toujours venir se confondre avec le
sommet de l’angle.
Ce point repère centre deux
traits qui, l’un quelconque, viendra se confondre avec
un côté de
l’angle donné ou à construire.
Une fois le rapporteur dans
cette position (point repère confondu avec le sommet de l’angle et un
des traits
confondu avec un côté de l’angle), je peux lire la mesure de l’angle donné ou
construire
un angle dont la mesure est donnée, à l’aide de l’une des
graduations.
Pour être utilisable, il doit satisfaire deux conditions :
1- Les graduations doivent être lisibles
2- Le point repère qui se trouve au milieu du bras droit doit être parfaitement lisible
Il me sert à trouver la
mesure d’un angle donné ; il me sert également à construire un angle dont
la
mesure est donnée.
Je comprends
Comment tracer une droite passant par un point donné ?
D’abord je dois choisir
l’instrument qui me permet de le faire. Sans aucun doute, cet instrument
est ma
règle.
Le point étant repéré sur ma
feuille de papier ou de dessin, je pose ma règle sur cette feuille en
veillant à
ce que son bord droit gradué passe par ce point ;
peu importe l’orientation de ma règle,
puisque c’est une,
parmi une infinité de droites, que je dois
tracer.
Ma règle, une fois dans cette position, avec mon crayon (bien taillé), je trace cette droite.
Ma feuille de dessin étant
limitée, je suis dans l’obligation d’arrêter, de part et d’autre, la droite.
Cependant, je retiendrai que ma droite est illimitée
dans les deux sens.
C’est pour cette raison que je nomme et
marque ses extrémités avec des lettres
minuscules x, y
ou u, v ou encore t, t’, en imaginant que ces points sont à
l’infini.
Ainsi, sur ma feuille de dessin, la droite tracée n’est qu’une représentation limitée de la droite géométrique exacte qui s’étend, de part et d’autre à l’infini.
Pour nommer ma droite dont les extrémités à l’infini sont les points x et y, j’écris :
(xy)
qui se lit « droite xy »
Conclusion :
Une droite (on dit aussi ligne droite) est illimitée.
Une infinité de droites passent par un point donné.
Pour tracer une droite j’utilise généralement une règle graduée.
Comment tracer la droite passant par deux points distincts donnés ?
L’instrument choisi pour cela est encore ma règle graduée.
Les points donnés étant
repérés sur ma feuille de papier ou de dessin, je pose ma règle sur cette
feuille en veillant à ce que son bord droit gradué passe
par ces deux points.
Cette fois, ma droite est unique ; il n’y en a pas
d’autres droites passant par ces deux points.
Ma règle, une fois dans cette position, avec mon crayon (bien taillé), je trace cette droite.
Celle-ci, comme
toute droite, est encore
illimitée ; j’imagine donc ses extrémités, les points x et y
par exemple,
sont à l’infini et, de part et d’autre de ma
droite je les marque.
J’écris :
(xy)
qui se lit « droite xy »
Si les deux points distincts sont par exemple A, B, je peux également écrire :
(AB)
qui se lit « droite AB »
Conclusion :
Une droite et une seule passe par deux points distincts
Pour tracer la droite passant par deux points distincts, j’utilise généralement une règle graduée.
Deux points
distincts étant donnés, comment tracer le segment de droite admettant comme
extrémités
ces deux points ?
L’instrument choisi pour cela est encore ma règle graduée.
Les points donnés étant
repérés sur ma feuille de papier ou de dessin, je pose ma règle sur cette
feuille en veillant à ce que son bord droit gradué passe
par ces deux points.
Ma règle, une fois dans cette position, avec mon crayon (bien taillé), je trace le segment de droite recherché.
Si, par exemple, les deux points sont A et B, alors j’écris :
[AB]
qui se lit « segment de droite AB »
Un segment de droite est
borné par ses deux extrémités.
C’est pour cette
raison qu’il a une mesure que je nomme longueur.
Pour trouver la longueur d’un segment de droite, j’utilise la graduation de ma règle graduée.
Conclusion :
Pour tracer le segment de droite passant par deux points distincts, j’utilise généralement une règle graduée.
Un point, par
exemple A, étant donné, et une droite, par exemple (xy), ne passant pas par A,
étant également donnée, comment construire la droite que je nommerai (d),
passant par A et perpendiculaire
à (xy) ?
J’ai le choix entre mon équerre et mon compas pour construire la droite (d).
Comment faire avec mon équerre ?
Je place l’équerre de manière que son plus petit bord droit vienne se confondre avec (xy).
En la maintenant dans cette position, je la fais glisser jusqu’à ce que l’autre bord droit passe par A.
Une fois l’équerre dans
cette nouvelle position, avec mon crayon, et
à partir du bord droit
passant par A, je trace la
droite (d).
Les deux bords droits de l’équerre formant un angle droit, (d) est donc perpendiculaire à (xy).
Comment faire avec mon compas ?
La pointe métallique du
compas étant placée en A, avec une ouverture de compas
suffisante,
je trace un arc de cercle coupant (xy) en deux points
distincts M et N.
La pointe métallique du
compas étant placée en M, avec une ouverture de compas
plus grande
que la moitié de la longueur de [MN], je trace dans la région
ne contenant pas A un arc de cercle
que je nomme,
par exemple, (l).
En gardant
cette dernière ouverture de compas, la
pointe métallique du compas étant placée en N,
je trace dans la région
ne contenant pas A un second arc de cercle que je
nomme, par exemple, (l’).
Les deux arcs de cercle (l) et (l’) se coupent en un point B.
Avec ma règle graduée, je trace la droite passant par A et B.
(AB) est la droite passant par A et perpendiculaire à (xy).
Un point, par exemple O, étant donné, et une droite, par exemple (tt’), ne passant pas par A, étant également donnée, comment construire la droite que je nommerai (xy), passant par O et parallèle à (tt’) ?
J’ai le choix entre mon équerre et mon compas pour construire la droite (d).
Comment faire avec mon équerre ?
Comme expliqué plus haut, je
trace d’abord avec mon équerre, la droite que je nommerai,
par exemple, (d),
passant par O et perpendiculaire à (tt’).
Par cette même
méthode, je trace la droite que je
nommerai, par exemple, (d’), passant par O
et perpendiculaire à (d).
(d’) et (tt’) étant perpendiculaires à (d) sont donc parallèles.
Ainsi, j’obtiens (d’) la droite passant par O et parallèle à (tt’).
Comment faire avec mon
compas ?
La pointe métallique du
compas étant placée en O, avec une ouverture de compas
suffisante,
je trace un arc de cercle coupant (tt’) en un point que je
nomme M. Je nomme (l) cet arc.
La pointe métallique du
compas étant placée en M, avec une ouverture de compas
égale à la
longueur de [OM], je trace un second arc de cercle coupant
(tt’) en un point que je nomme N.
Je nomme (l’) cet arc.
Je prends l’ouverture de compas égale à la longueur de [ON].
La pointe métallique étant placée en M, avec cette ouverture de compas, je repère et marque le point, nommé par exemple P, situé dans la région contenant O et appartenant à l’arc (l).
Avec ma règle graduée, je trace (OP), la droite passant par O et parallèle à (tt’).
Un segment étant donné, comment tracer sa médiatrice ?
Je sais que la médiatrice d’un segment est la droite qui passe par son milieu et qui lui est perpendiculaire.
On me donne [AB] et on me demande de construire sa médiatrice, que je nomme, par exemple, (d).
Je choisis le compas comme instrument.
La pointe métallique du compas placée sur une extrémité quelconque de [AB], par exemple A, avec une ouverture de compas plus grande que la moitié de la longueur de [AB], je trace, de part et d’autre de (AB), deux arcs de cercles que je nomme, par exemple, (m) et (m’).
En conservant
cette ouverture de compas, la pointe
métallique placée en B, je trace, de part et d’autre
de
(AB), deux autres arcs de cercle que je nomme, par exemple, (u) et (v).
Ces quatre arcs se coupent deux à deux aux points M et N.
Avec ma règle graduée, je trace (MN) qui sera la médiatrice de [AB].
Remarque :
(MN) étant la médiatrice de [AB], elle coupera ce dernier en son milieu O.
Donc, en construisant la médiatrice d’un segment, je trouve la position exacte de son milieu.
Un angle étant donné, comment construire sa bissectrice ?
Je sais que la bissectrice d’un angle est la demi-droite ayant pour origine le sommet de cet angle et partageant ce dernier en deux angles de même mesure.
Ainsi, si la mesure de
l’angle donné est égale à 62°, alors sa bissectrice le partagera en deux angles
ayant 31° pour mesure commune.
Pour tracer la bissectrice d’un angle, je choisis le compas comme instrument.
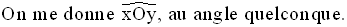
On me demande de tracer sa bissectrice.
Je sais que cette bissectrice est une demi-droite d’origine le sommet O de cet angle.
La pointe métallique du compas
étant placée en O, avec une ouverture de compas quelconque,
je trace un arc de
cercle rencontrant les deux côtés [Ox) et [Oy) de l’angle donné, respectivement
aux points que je nomme, par exemple, M et N.
La pointe métallique du compas
placée en M, avec une ouverture de compas quelconque,
je trace un arc de cercle
que je nomme, par exemple, (l).
En conservant cette
dernière ouverture de compas, la pointe
métallique étant placée en N,
je trace un second arc de cercle que je nomme, par
exemple, (l’).
Les deux arcs de cercles (l) et (l’) se coupent au point que je nomme, par exemple, P.
Avec ma règle graduée, je trace la demi-droite [Op) qui sera la bissectrice recherchée.
Jai évidement :
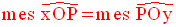
Un angle étant dessiné, comment je trouve sa mesure ?
Pour trouver la mesure d’un angle dessiné, je choisis le rapporteur comme instrument.
D’abord, pour mieux utiliser
le rapporteur, je prolonge suffisamment les deux côtés [Ox) et
[Oy) de l’angle.
Je place le rapporteur de manière que son point repère vienne se confondre avec le sommet O de l’angle.
Je fais
confondre un des traits centrés par le point repère avec
un des côtés de l’angle,
par exemple [Ox).
Je repère le trait d’une des
graduations en degrés du rapporteur par lequel passe l’autre côté [Oy).
Je lis
la valeur correspondante à ce trait ; cette valeur me donne la mesure de
l’angle.
Deux figures illustrant cette lecture

Une mesure d’angle étant donnée, comment je construis un angle ayant cette mesure ?
Pour construire un angle dont la mesure est donnée, je choisis le rapporteur comme instrument.
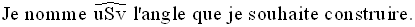
Je trace une demi-droite quelconque [Su), d’origine S (j’aurai pu la nommer [Sv), ça n’a aucune importance).
Je place le rapporteur de
manière que son point repère vienne se confondre avec le
sommet S de
l’angle à construire.
Je fais confondre un des traits centrés par le point repère avec [Su).
Le rapporteur dans cette
position, je repère le trait d’une des graduations en degrés qui
correspond
à la mesure donnée.
Avec le crayon, je
marque le point qui correspond à ce trait ; je nomme M ce point.
Avec la règle graduée, je trace [SM) qui sera l’autre côté [Sv) de l’angle à construire.
J’obtiens ainsi l’angle recherché dont la mesure est égale à celle donnée.

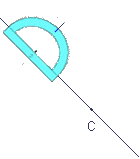
Etape 1
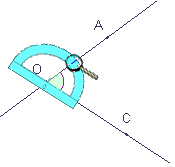
Etape 2
Les trois longueurs des trois côtés d’un triangle étant données, comment construire ce triangle ?
Soient a, b et c les longueurs des trois côtés d’un triangle (s’il existe) données, par exemple en centimètres.
Pour construire ce triangle, je choisis le compas comme instrument.
Je trace un segment, que je nomme, par exemple [AB], dont la longueur est l’une quelconque choisie parmi a, b et c, par exemple a. Pour cela j’utilise ma règle graduée.
La pointe métallique du
compas étant placée en A (j’aurai pu le faire en B, ça n’a aucune importance),
avec une ouverture du compas égale à b (j’aurai pu choisir c, ça n’a aucune
importance),
je trace un arc de cercle que je nomme (l).
La pointe métallique du
compas étant placée en B, avec une ouverture du compas égale à c,
je trace un
arc de cercle que je nomme (l’).
Deux cas de figure peuvent se présenter :
les deux arcs de cercle (l) et (l’) ne se rencontrent pas ; je dis alors que le triangle demandé n’existe pas.
les deux arcs de cercle (l)
et (l’) se coupent au point que je nomme C.
Le triangle recherché est donc (ABC).
Les longueurs de
deux côtés d’un triangle et la mesure de l’angle qu’ils forment, étant données,
comment je construis ce triangle ?
Soient a et b les longueurs de deux côtés d’un triangle, données.
La mesure de l’angle que forment ces deux côtés est également donnée.
Pour construire ce triangle, je choisis le compas et le rapporteur comme instruments.
Avec mon rapporteur, je construis un angle dont la mesure est égale à la mesure d’angle donné.

La pointe métallique du
compas étant placée en A, avec une ouverture de compas égale à a,
je trace un
arc de cercle qui vient couper [Ax) au point que je nomme B.
La pointe métallique du
compas maintenue en A, avec une ouverture de
compas égale à b,
je trace un arc de cercle qui vient couper [Ay) au point que
je nomme C.
Le triangle demandé est donc (ABC).
Les mesures de deux angles d’un triangle et la longueur du côté commun à ces angles, étant données, comment je construis ce triangle ?
Soit a la longueur du côté commun à ces deux angles.
Pour construire ce triangle, je choisis le rapporteur comme instrument.
Je trace un segment, que je
nomme, par exemple, [AB], dont la longueur est égale à a, donnée.
Pour cela
j’utilise ma règle graduée.
Avec mon rapporteur et à
partir du point A [point repère confondu avec A et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (AB)], je repère le trait
d’une des graduations
du rapporteur correspondant à une des deux mesures d’angle
données :

Je repère, par exemple, le trait correspondant à la mesure :
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple M, ce point.
Avec ma règle graduée, je trace [AM).
Avec mon rapporteur et à
partir du point B [point repère confondu avec B et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (AB)], je repère le trait
d’une des graduations
du rapporteur correspondant à l’autre mesure d’angle
donnée :
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple N, ce point.
Avec ma règle graduée, je trace [BN).
[AM) et [BN) se coupent en un point que je nomme C.
Le triangle demandé est donc (ABC).
Je m’exerce
Vrai ou faux ?
Parmi les phrases suivantes lesquelles sont vraies ?
- Pour mesurer un angle j’utilise mon rapporteur.
- Pour construire un segment dont la longueur m’est donnée j’utilise ma règle graduée.
- Pour tracer la bissectrice d’un angle donné j’utilise mon rapporteur.
- Pour construire la médiatrice d’un segment j’utilise mon compas.
- Je peux construire un triangle dont les longueurs des côtés sont 4cm, 3cm et 9cm.
Solution
Les deux premières phrases et la quatrième sont vraies.
Pour tracer la bissectrice d’un
angle donné j’utilise mon compas.
La troisième phrase est donc
fausse.
Les deux arcs de cercle
correspondants respectivement aux deux ouvertures de compas de 3cm
et 4cm ne se
coupent pas ; le triangle n’existe pas.
La dernière phrase est donc
fausse.
On me donne les figures suivantes dessinées à main levée. On me demande de les reconstruire en utilisant les instruments adéquats :
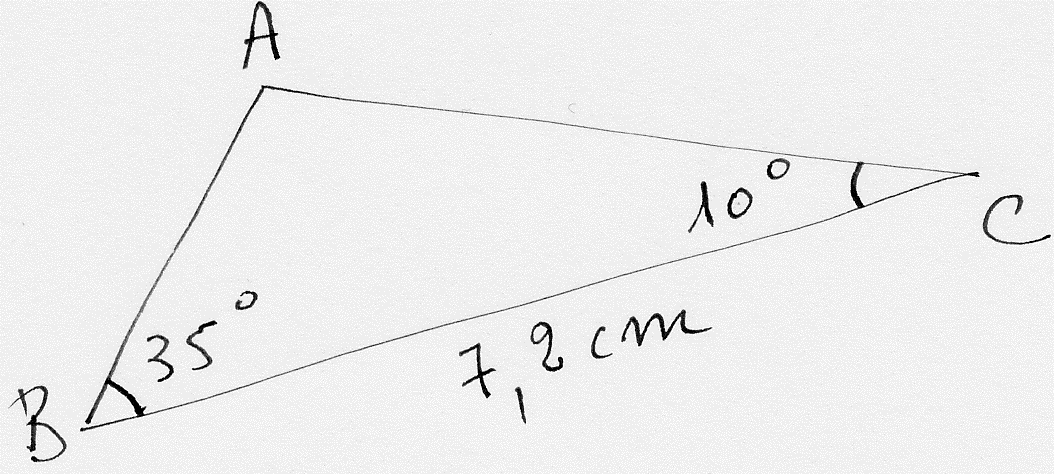
Figure 1

Figure 2

Figure 3
PQ = 4cm, QR = 7cm et PR = 5cm
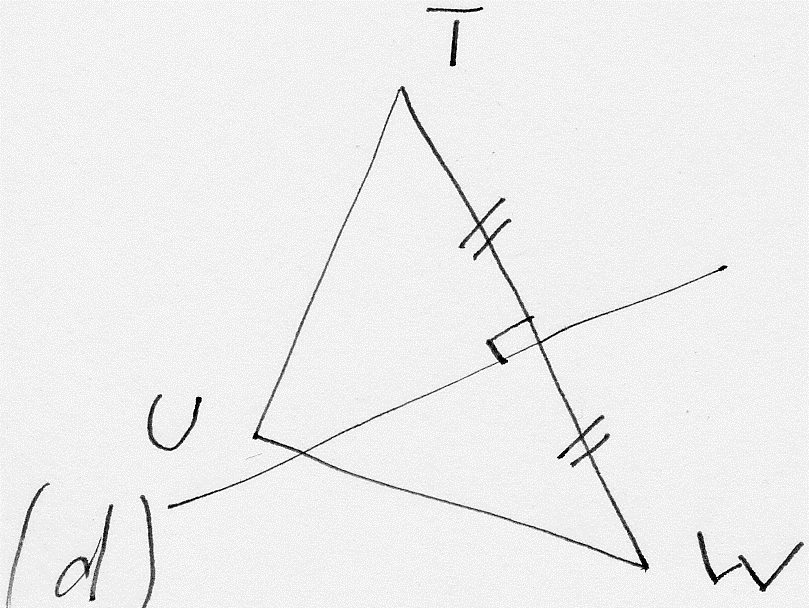
Figure 4
TW = 5cm, UW = 7cm et UT = 4cm

Figure 5
Solution
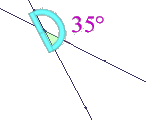
Pour la figure 1
Pour construire ce triangle, je choisis le rapporteur comme instrument.
Je trace un segment, que je
nomme, par exemple, [BC], dont la longueur est égale à 7,2cm.
Pour cela
j’utilise ma règle graduée.
Avec mon rapporteur et à
partir du point B [point repère confondu avec B et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (BC)], je repère le trait
d’une des graduations
du rapporteur correspondant à 35°.
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple M, ce point.
Avec ma règle graduée, je trace [BM).
Avec mon rapporteur et à
partir du point C [point repère confondu avec C et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (BC)], je repère le trait
d’une des graduations
du rapporteur correspondant à l’autre mesure d’angle
donnée : 10°
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple N, ce point.
Avec ma règle graduée, je trace [CN).
[BM) et [CN) se coupent en un point que je nomme A.
Le triangle demandé est donc (ABC).
Pour la figure 2
Pour construire ce triangle, je choisis le compas et le rapporteur comme instruments.
Avec mon rapporteur, je construis un angle dont la mesure est égale à 45°.
La pointe métallique du
compas étant placée en N, avec une ouverture de compas égale à 3,2cm,
je trace
un arc de cercle qui vient couper [Nx) au point que je nomme M.
La pointe métallique du
compas maintenue en N, avec une ouverture de
compas égale à 5cm,
je trace un arc de cercle qui vient couper [Ny) au point que
je nomme P.
Le triangle demandé est donc (MNP).
Pour la figure 3
Pour construire ce triangle, je choisis le compas comme instrument.
Je trace un segment, que je nomme [QR], dont la longueur est égale à 7cm.
Pour cela j’utilise ma règle graduée.
La pointe métallique du
compas étant placée en Q, avec une ouverture du compas égale à 4cm,
je trace un
arc de cercle que je nomme (l).
La pointe métallique du
compas étant placée en R, avec une ouverture du compas égale à 5cm,
je trace un
arc de cercle que je nomme (l’).
Les deux arcs de cercle (l) et (l’) se coupent au point que je nomme P.
Le triangle recherché est donc (PQR).
Le codage donné sur la
figure m’indique que la demi-droite [Px) est la bissectrice de l’angle
intérieur
en P du triangle (PQR).
La pointe métallique du
compas étant placée en P, avec une ouverture de compas quelconque,
je trace un
arc de cercle rencontrant les deux côtés [PQ) et [PR) de l’angle donné,
respectivement aux points que je nomme, par exemple, M et N.
La pointe métallique du compas
placée en M, avec une ouverture de compas quelconque,
je trace un arc de cercle
que je nomme, par exemple, (l).
En conservant cette
dernière ouverture de compas, la pointe
métallique étant placée en N,
je trace un second arc de cercle que je nomme, par
exemple, (l’).
Les deux arcs de cercles (l) et (l’) se coupent au point que je nomme, par exemple, F.
Avec ma règle graduée, je trace la demi-droite [PF) qui sera la bissectrice recherchée.
Pour la figure 4
Pour construire cette figure, je choisis le compas comme instrument.
Je construis d’abord le triangle (TUW).
Je trace un segment, que je nomme [UW], dont la longueur est égale à 7cm.
Pour cela j’utilise ma règle graduée.
La pointe métallique du
compas étant placée en U, avec une ouverture du compas égale à 4cm,
je trace un
arc de cercle que je nomme (l).
La pointe métallique du
compas étant placée en W, avec une ouverture du compas égale à 5cm,
je trace un
arc de cercle que je nomme (l’).
Les deux arcs de cercle (l) et (l’) se coupent au point que je nomme T.
Le triangle recherché est donc (UWT).
Le codage donné sur la figure m’indique que la droite (d) est la médiatrice de [TW].
Pour construire (d), je procède comme suit :
La pointe métallique du
compas placée sur une extrémité quelconque de [TW], par exemple T,
avec
une ouverture de compas plus grande que la moitié de la
longueur de [TW], je trace,
de part et d’autre de
(TW), deux arcs de cercles que je nomme, par exemple, (m) et (m’).
En conservant
cette ouverture de compas, la pointe
métallique placée en W, je trace, de part et
d’autre de
(TW), deux autres arcs de cercle que je nomme, par exemple, (u) et (v).
Ces quatre arcs se coupent deux à deux aux points M et N.
Avec ma règle graduée, je trace (MN) = (d) qui sera la médiatrice de [TW].
Pour la figure 5
Pour construire cette figure, je choisis le rapporteur comme instrument.
Je trace un segment, que je nomme [JK], dont la longueur est égale à 4,2cm.
Pour cela j’utilise ma règle graduée.
Avec mon rapporteur et à
partir du point J [point repère confondu avec J et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (JK)], je repère le trait
d’une des graduations
du rapporteur correspondant à 125°.
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple R, ce point.
Avec ma règle graduée, je trace [JR).
Sur cette demi-droite, avec ma règle graduée, je marque le point M tel que JM = 5cm.
Avec mon rapporteur et à
partir du point K [point repère confondu avec K et, un des deux traits du
rapporteur centrés par le point repère, confondu avec (JK)], je repère le trait
d’une des graduations
du rapporteur correspondant à 90°.
Je marque avec mon crayon le point qui correspond à ce trait. Je nomme, par exemple R’, ce point.
Avec ma règle graduée, je trace [KR’).
Sur cette demi-droite, avec ma règle graduée, je marque le point L tel que KL = 9cm.
Avec ma règle graduée, je trace [LM].
Le quadrilatère (JKLM) ainsi construit est celui recherché.
On te donne un triangle quelconque (ABC).
Construis la bissectrice [Bx) de l’angle intérieur en B de ce triangle.
Construis la bissectrice [Cy) de l’angle intérieur en C de ce triangle.
Nomme I le point de rencontre de ces deux bissetrice.
Que constates-tu pour la demi-droite [AI) ? Qu’en déduis-tu ?
Solution
Comme expliqué plus haut, avec mon compas, je construis les bissectrices [Bx) et [Cy) respectivement des angles intérieurs en B et en C de ce triangle.
Je nomme I l’intersection de ces deux bissectrices.
Je joins A à I.
Avec mon rapporteur, je constate que les angles suivants :

ont même mesure.
Par conséquent, [AI) est la bissectrice du troisième angle intérieur en A de ce triangle.
J’en déduis que :
dans un triangle, les trois bissectrices de ses trois angles intérieurs sont concourantes en un point.
Trace un une droite quelconque que tu nommeras (xy).
Marque un point quelconque sur cette droite que tu nommeras O.
Trace la demi-droite [Oz) faisant avec [Ox) un angle ayant 124° pour mesure.


Que constates-tu pour l’angle formé par ces deux bissectrices ? Peux-tu le prouver ?
Solution
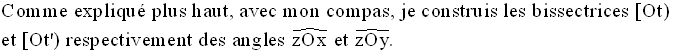
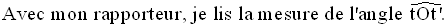
Je constate que cet angle est droit.
Je le démontre.