L'EXERCICE
POUR LA SECONDE ET LA PREMIERE S
(page 5)
les thèmes abordés dans cette page
dans un atelier de
fabrication de pièces mécaniques
(2de)
résolution graphique
d'une équation
(2de)
propriété d'un
quadrilatère quelconque
(2de)
perpendiculaire commune
à deux droites quelconques de l'espace
(1ère S)
dans un atelier de
fabrication de pièces mécaniques
(groupe ciblé : seconde)
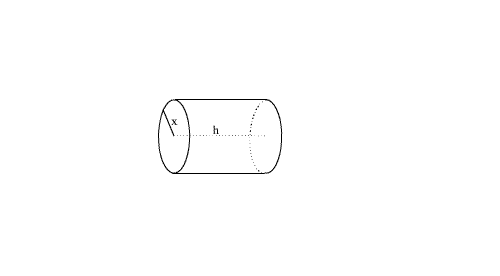
Dans
un atelier de fabrication de pièces mécaniques, on souhaite fabriquer une cuve
cylindrique en tôle.
Sa
hauteur est h et le rayon de sa base circulaire est x.
x
et h sont exprimés en décimètres.
Soient
V et S respectivement le volume et la surface totale, en tôle, de cette cuve.
1)
Exprime V en fonction de x et h, puis S en fonction de x et V.
2)
Pour V = 2000 litres, quelle valeur donner à x pour que la surface totale S
soit minimale ?
3)
On souhaite que la surface totale en tôle n’excède pas 2000 dm2 .
Dans quel intervalle doit donc varier le rayon x ?
Solution

1)
Exprimons
V en fonction de x et h, puis S en fonction de x et V.
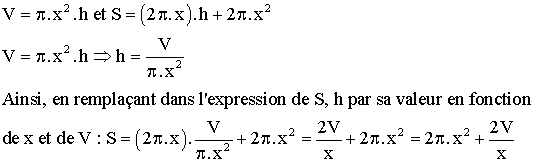
2)
Pour
V = 2000 litres, calculons la valeur à donner à x pour que la surface totale S
soit minimale.
Remplaçons
dans l’expression de S en fonction de x et de V, V par 2000 litres ou 2000 dm3
.
![]()
S
est donc une fonction numérique dont la variable est le rayon x.
![]()
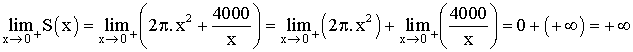
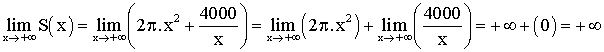
Calculons
la dérivée de S(x).
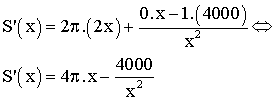
Étudions le signe de cette dérivée.
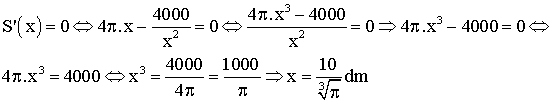
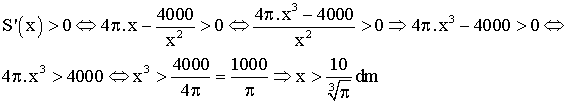

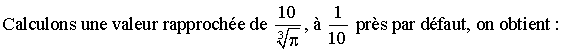
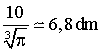
Ainsi,
S’(x) < 0 pour x appartenant à ]0 ; 6,8[, S’(6,8) = 0 et S’(x)
> 0 pour
x
> 6,8.
Donc
S est strictement décroissante sur l’intervalle ]0 ; 6,8[, strictement
croissante pour x > 6,8 et admet un minimum égal à S(6,8).
Conclusion :
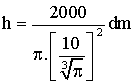
![]()
3)
On
souhaite que la surface totale en tôle n’excède pas 2000 dm2 ,
toujours pour une capacité V = 2000 dm3 . Trouvons alors
l’intervalle dans lequel doit varier le rayon x.
Cette
condition se traduit par :
![]()
En
rassemblant tous les termes de cette inéquation dans le premier membre et en
mettant au même dénominateur x (on ne change pas le sens de l’inéquation
puisque x est strictement positive), on obtient :
![]()
Comme
x > 0, cette fraction est négative lorsque son numérateur l’est ;
donc :
![]()
C’est
une inéquation du troisième degré en x. Pour éviter sa résolution (hors
programme de seconde), il faudra utiliser sa résolution graphique.
Pour
cela, nous construisons la courbe C représentative de la fonction S(x) et la
droite d d’équation S0 = 2000, dans un repère orthogonal.
d coupe C en deux points M et N dont les abscisses seront les extrémités de
l’intervalle dans lequel doit varier x.
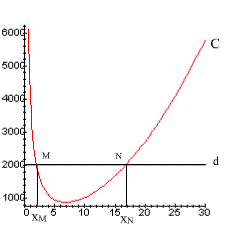
La droite
d d’équation S0 = 2000 rencontre C aux points M et N d’abscisses :
![]()
Donc
S ne dépassera pas la valeur 2000 si x varie dans l’intervalle ]2,02 ;
16,7[.
Recommandation : pour pouvoir lire les abscisses de M et N, il est fortement conseillé de tracer les courbes sur un papier millimétré.
résolution graphique
d'une équation
(groupe ciblé : seconde)
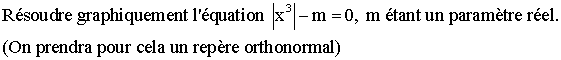
Solution
L’équation
peut se mettre sous la forme :
![]()
Ainsi,
pour la résoudre graphiquement il suffit de construire la courbe C représentative
de la fonction :
![]()
Puis
de tracer la droite d parallèle à l’axe des abscisses en vue de la faire
varier.
![]()
f
est définie et continue sur R.
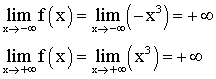
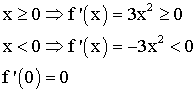
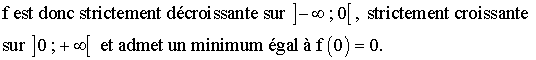
On
obtient ainsi le graphique suivant :

d
ayant la position d0 , rencontre la courbe C en deux points distincts
symétriques par rapport à l’axe des ordonnées ; ce qui correspond donc
à
m > 0.
Ainsi pour m > 0, l’équation possède deux racines réelles distinctes et
opposées.
d
ayant la position d1 , rencontre C en un seul point, origine du repère ;
ce qui correspond à m = 0.
Ainsi pour m = 0, l’équation admet une racine réelle et une seule.
d
ayant la position d2 , ne rencontre pas C; ce qui correspond à
m < 0.
Ainsi pour m < 0, l’équation n’admet aucune
racine réelle.
propriété d'un
quadrilatère quelconque
(groupe ciblé : seconde)
On
donne un quadrilatère quelconque (ABCD).
Soient
M et N les milieux respectifs des deux côtés opposés [BC] et [AD]. Soit W le
milieu de [MN].
1)
Que représente W pour (ABCD) ?
2)
Montre que W est aligné avec les milieux P et Q des deux autres côtés [AB] et
[CD].
3)
En déduis la nature du quadrilatère (MPNQ).
Solution
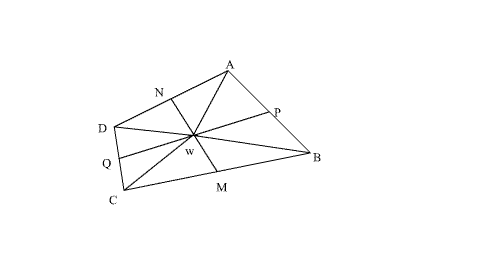
1)
Dans
le triangle (DWA), [WN] est médiane relative au côté [DA] ; donc on a :
![]()
Dans
le triangle (BWC), [WM] est médiane relative au côté [BC] ; donc on a :
![]()
Mais
W étant milieu du segment [MN], on a :
![]()
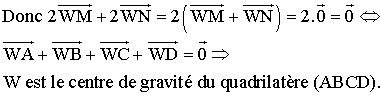
2)
Dans
le triangle (WAB), [WP] est médiane relative au côté [AB] ; donc on a :
![]()
Dans
le triangle (WCD), [WQ] est médiane relative au côté [CD] ; donc on a :
![]()
Ainsi
on a :
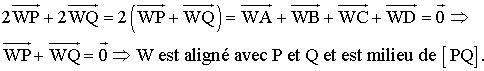
3)
Dans
le quadrilatère (MPNQ), W est simultanément milieu des diagonales [MN] et [PQ].
On sait que si les diagonales d’un quadrilatère ont même milieu, alors ce
quadrilatère est un parallélogramme.
Donc (MPNQ) est un parallélogramme.
perpendiculaire commune
à deux droites quelconques de l'espace
(groupe ciblé : première S)
On
considère deux droites de l’espace (D) et (D’) et leur perpendiculaire
commune (OO’), O appartenant à (D) et O’, à (D’).
Soient
M un point variable de (D) et N un point variable de (D’).
Partie
1
a) Trouve le lieu géométrique du point I milieu de [MN].
b) Trouve
l’ensemble des points E appartenant à (MN) et tels que :
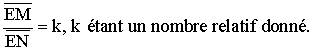
Partie
2
On
pose OO’ = 4a, a étant un nombre strictement positif ; OM = z et O’N =
2z.
Calcule MN en fonction de a et z dans les deux cas suivants :
1- (D) et (D’) sont orthogonales ;
2- (D) et (D’) forment entre elles un angle de 45°.
Solution
Partie
1
a)
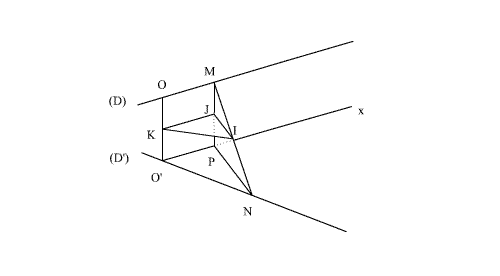
Du
point O’ menons la droite (O’x) parallèle à (D).
Dans
le plan [(O’x) ;(D)] soit P la projection orthogonale de M sur (O’x).
Soient
J et K les milieux respectifs des segments [MP] et [OO’].
Dans
le plan [(O’x) ;(D)], (OO’) étant perpendiculaire à (D) et (D) étant
parallèle à (O’x), alors (OO’) est perpendiculaire à (O’x).
Mais (MP) est perpendiculaire à (O’x).
Donc (MP) et (OO’) sont parallèles.
Ainsi (MP) étant parallèle à (OO’) et (D) étant parallèle à (O’x), (OMPO’)
est alors un parallélogramme ; de plus, (OO’) étant perpendiculaire à
(O’x), ce parallélogramme est un rectangle.
Dans
le rectangle (OMPO’), le segment joignant les milieux J et K des côtés [MP]
et [OO’], est perpendiculaire à (OO’).
Dans
le triangle (MPN), I et J étant milieux respectifs des côtés [MN] et [MP], le
segment [IJ] est parallèle à (PN).
(OO’)
étant la perpendiculaire commune de (D) et (D’), alors (OO’) est
perpendiculaire à (D’) et (O’x), deux droites concourantes du plan
[(O’x) ;(D’)] ; donc (OO’) est orthogonale à ce plan et
ainsi à toute droite de ce plan, en particulier à (PN).
(OO’)
étant perpendiculaire à (PN) et (IJ) étant parallèle à (PN), alors (OO’)
est perpendiculaire à (IJ).
(OO’)
étant perpendiculaire aux deux droites concourantes (IJ) et (JK) du plan (IJK),
alors (OO’) est orthogonale au plan (IJK).
O
et O’ étant fixes, le milieu K de [OO’] l’est également.
Ainsi
le plan (IJK) est orthogonal à la droite fixe (OO’), au point fixe K, milieu
de [OO’].
Donc (IJK) est le plan médiateur du segment fixe [OO’] ; l’ensemble
des points I est donc le plan (IJK).
b)
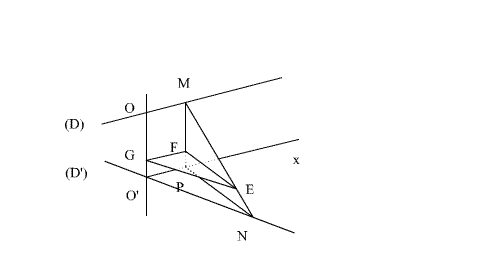
Soit
le plan passant par E et parallèle
au plan médiateur de [OO’]. Il rencontre (MP) et (OO’) respectivement aux
points F et G.
Ce plan est donc orthogonal à (OO’).
Ainsi
les plans [(O’x) ;(D’)] et (EGF) étant orthogonaux à (OO’),
sont parallèles ; tout plan les coupant, les rencontrera selon deux
intersections parallèles.
Ainsi, le plan (MPN) rencontre les plans parallèles [(O’x) ;(D’)] et
(EGF) selon les droites parallèles (EF) et (PN).
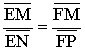
Le plan [(D) ;(O’x)]
rencontre les plans parallèles [(O’x) ;(D’)] et (EGF)
selon les droites parallèles (GF) et (O’P).
Dans le rectangle (OMPO’), on a donc (GF) parallèle à (O’P) et le théorème
de Thalès donne :
Finalement,
on a :


L’ensemble
des points E est donc le plan fixe (EGF) orthogonal à la droite fixe (OO’) et
rencontrant cette dernière au point fixe G.
Partie
2
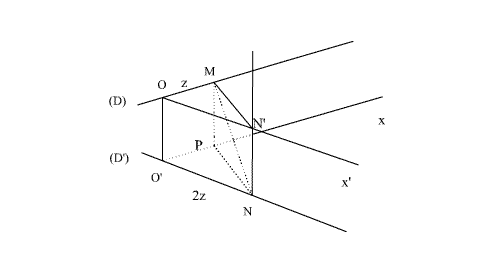
Dans
le plan [O ; (D’)] menons de O la parallèle (Ox’) à (D’). Puis plaçons
le projeté orthogonal N’ de N sur (Ox’).
(ON’) est parallèle à (O’N).
(OO’) étant orthogonale à (D’), est orthogonale à (Ox’).
(OO’) étant orthogonale à (Ox’) et (NN’) étant orthogonale à (Ox’),
alors (OO’) est parallèle à (NN’).
(ON’)
étant parallèle à (O’N) et (OO’) étant parallèle à (NN’), (OO’NN’)
est un parallélogramme et ainsi OO’ = NN’ = 4a.
(NN’) étant parallèle à (OO’) et (OO’) étant orthogonale au plan [(D) ; (Ox’)], alors (NN’) est orthogonale à ce plan, donc à toute droite de ce plan et en particulier à (MN’).
Ainsi, le
triangle (MNN’) est rectangle en N’ et le théorème de Pythagore donne :
![]()
1-
(D) et (D’) sont orthogonales
![]()
Mais dans
le parallélogramme (OO’NN’), O’N = N’O = 2z ;
donc on a :
![]()
Donc on a :
![]()
2-
(D) et (D’) forment entre elles un angle de 45°.
![]()
Dans le
triangle (N’OM) on a la relation métrique :
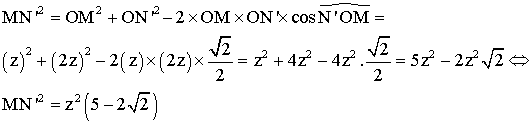
Donc on a :
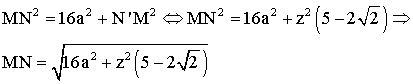
page 1 page 2 page 3 page 4 page 6