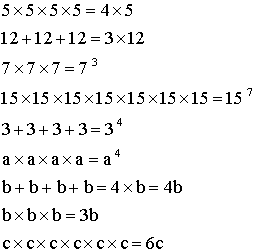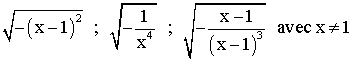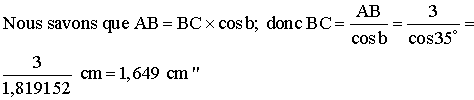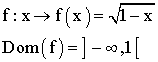CE QU'IL NE FAUT PAS FAIRE

CE QU'IL NE FAUT PAS FAIRE

les thèmes abordés dans cette page

priorités des opérations
(4ème)

opérations sur les unités de temps
(6ème et 5ème)

géométrie du polygone
(6ème)

simplifier une expression
(5ème)

développement-factorisation ; racine carrée
(3ème)

fonction cosinus
(4ème)

logique et fonction numérique
(premières, toutes séries confondues)

dérivées et primitives
(terminales)

priorités des opérations
(groupe ciblé : quatrième)

Souvent tu confonds les expressions suivantes :

a×bⁿ et (a×b)ⁿ ; a+b×c et (a+b)×c.

Effectue 5×3².
Si tu multiplies 5 par 3 et tu élèves le résultat à la puissance 2 ; c'est-à-dire
15² = 225, ta réponse est fausse.

En l'absence de parenthèses, la puissance est prioritaire par rapport à la multiplication.
Dans a×bⁿ, d'abord tu élèveras b à la puissance n, ensuite tu multiplieras le résultat par a.
Ainsi 5×3² = 5×9 = 45.

Par contre dans (a×b)ⁿ, en présence des parenthèses la multiplication a×b est devenue prioritaire ; tu effectueras d'abord a×b puis ensuite tu élèveras le résultat à la puissance n.
Ainsi (5×3)² = 15² = 225.

Effectue 5+3×4.
Si tu additionnes 5 et 3 puis tu multiplies le résultat par 4, la réponse est fausse.

En l'absence de parenthèses, la multiplication est prioritaire par rapport à l'addition ou à la soustraction.
Dans a+b×c (ou a-b×c), d'abord tu effectueras la multiplication b×c, ensuite tu ajouteras le résultat à a
(ou tu le retrancheras de a).
Ainsi 5+3×4 = 5+12 = 17.

Par contre dans (a+b)×c, en présence des parenthèses l'addition est devenue prioritaire ; tu effectueras d'abord a+b puis ensuite tu multiplieras le résultat par c.
Ainsi (2+4)×7 = 6×7 = 42.
Il en sera de même pour (a-b)×c.

retour au début de la page

opérations sur les unités de temps
(groupes ciblés : sixième et cinquième)

L'heure contient 60 minutes et la minute contient 60 secondes.

Le symbole de l'heure est h ; celui de la minute est min et celui de la seconde est s.

Les heures, minutes et secondes s'additionnent séparément ; il en est de même pour la soustraction et la multiplication par un entier naturel.

Ainsi, dans l'addition suivante :

2h 50min 53s
+
3h 54min 52s
___________

6h 05min 05s

opérer sans tenir compte des unités de temps et de la conversion de l'une à l'autre est une erreur ; l'addition ne se fait pas comme si tu opérais sur des nombres décimaux ou entiers naturels.

Tu devras d'abord additionner les quantités ayant la même unité de temps ; c'est-à-dire les heures avec les heures, les minutes avec les minutes et les secondes avec les secondes.
Puis ensuite, tu procèderas à l'extraction des quantités de secondes ou de minutes convertissables respectivement en minutes et en heures.

Dans l'exemple ci-dessus, on obtient donc :

5h 104min 105s

105s = 60s + 45s ; 105s valent 1min 45s et ainsi
5h 104min 105s = 5h (104+1)min 45s = 5h 105min 45s

105min = 60min + 45min = 1h 45min
Donc 5h 105min 45s = (5+1)h 45min 45s = 6h 45min 45s

Prends la multiplication suivante :

3h 45min 58s
x
4
______________
13h 82min 32s

Elle est fausse puisqu'on a opéré comme si les unités de temps n'existaient pas.

Comment d'après toi fallait-il procéder ?

Prends la division suivante à effectuer :

13h 27min 56s ÷ 2

Là également la réponse telle que 6,5h 13,5min 28s est fausse.

Comment procèdes-tu ?

D'abord tu divises 13 par 2 ; le quotient est 6h et le reste est 1h.

Ce quotient 6 est la première partie de la réponse.

Le reste 1h est converti en minutes et le résultat, ajouté à 27min.
Tu obtiens 60min + 27min = 87min.
Tu divises 87 par 2 ; le quotient est 43min qui sera la seconde partie de ta réponse ;
le reste 1min est converti en seconde et le résultat, ajouté à 56s. Tu obtiens 60s + 56s = 116s.

Tu divises 116 par 2 et tu obtiens 58s qui représente la dernière partie de la réponse recherchée .

La réponse est donc : 6h 43min 58s .

retour au début de la page

géométrie du polygone
(groupe ciblé : sixième)

Une ligne brisée n'est pas uniquement une suite de segments dans un plan.

Dis pourquoi cet énoncé manque de précision et corrige-le.

Un camarade de classe écrit :

1- Un polygone est un objet d'un plan délimité par une ligne brisé.
2- Un pentagone est un polygone de 6 côtés.
3- Un quadrilatère est un polygone de quatre côtés.
4- Le carré est un quadrilatère.
5- Dans un polygone, une diagonale est une droite joignant deux sommets opposés.
6- Dans un polygone, il y a autant de sommets que de côtés. Ainsi, si le polygone possède n côtés, alors il possède n sommets.
7- Un hexagone est un polygone possédant six côtés, donc :

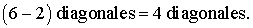
8- Un polygone de n côtés possède (n - 2) diagonales.
9- Un décagone est un polygone possédant 8 côtés et un octogone est un polygone possédant dix côtés.
10- Tout carré est un parallélogramme.
11- Tout rectangle est un parallélogramme.
12- Dans un parallélogramme, deux côtés opposés sont parallèles et de même mesure géométrique.
13- Pour démontrer qu'un quadrilatère est un parallélogramme, il suffit de démontrer que deux côtés opposés quelconques sont parallèles.
14- Un losange est un carré.
15- Un carré est un losange dont les angles sont tous droits.

On te demande de lui corriger cette page.

simplifier une expression
(groupe ciblé : cinquième)

1- Lors de la simplification des expressions, il ne faudra pas confondre une opération sur les puissances ou exposants et celle portant sur l'addition d'une même quantité.

Exemples :

L'expression 3 + 3 + 3 + 3 qui se simplifie en écrivant 3 x 4 est différente de l'expression
3 x 3 x 3 x 3 qui se simplifie en écrivant :

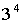
Un élève de ta classe a simplifié les expressions suivantes en écrivant :

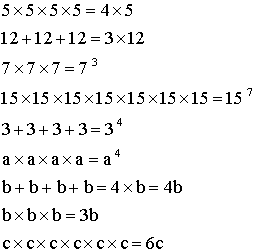
On te demande de corriger cette page.

développement-factorisation ; racine carrée
(groupe ciblé : troisième)

1- Lors du développement d'une expression, on a souvent oublié de tenir compte des règles
liées aux signes :

le produit de deux nombres de même signe (+ ou -) est positif ; celui de deux nombres de signes
contraires ou opposés est négatif.

Tu lis dans un cahier d'un de tes camarades les développements suivants :
(2x - 5)(-3x - 2) = -6x² + 4x + 15x - 10 = -6x² + 19x - 10 ;
(-3x - 2)² = 9x² - 12x + 4 .
Explique lui ce qu'il ne fallait pas faire et corrige lui les résultats .

Au cours d'une factorisation, l'erreur qu'il ne faut pas faire est d'ignorer ces règles qui s'appliquent également à la division .
Exemples d'erreur :
4x² - 24x + 9 = (-2x - 3)² ;
(2x + 1)(-3x + 1) - (x +1)(1- 3x) - 2(3x + 2)(3x - 1) = (-3x + 1)(2x + 1- x + 1- 6x - 4) =
(-3x + 1)(-5x - 2) .
Explique ce qu'on ne devait pas faire lors de ces factorisations et corrige les résultats .

2- Peux - tu trouver un nombre entier ou décimal relatif tel que son carré soit égal à -2 ?
Lorsque tu travailles dans l'ensemble des nombres entiers relatifs ou dans l'ensemble des nombres décimaux relatifs, la racine carrée d'un nombre strictement négatif n'existe pas.

Dans ces ensembles , des écritures telles que :

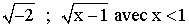
sont toutes fausses.

Explique comment la dernière expression est déclarée fausse ? Comment peux - tu la rectifier ?

Pourquoi les expressions suivantes n'ont aucun sens si on les considère dans l'ensemble des nombres décimaux relatifs ?

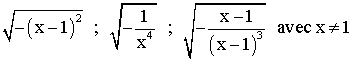
retour au début de la page

fonction cosinus
(groupe ciblé : quatrième)

Le cosinus d'un angle aigu est toujours largement inférieur à 1.

Ainsi, lors d'un calcul, un résultat tel que cos(A) = 1,745 est faux.

On lit dans un cahier d'un élève de quatrième le passage suivant : "

(ABC) est un triangle rectangle en A.
AB = 3 cm et les mesures de ses angles aigus en B et en C sont respectivement b et c.
b = 35°

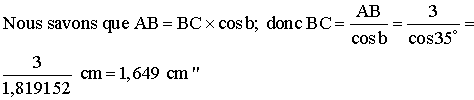
Trouve l'erreur commise et rectifie.

retour au début de la page

logique et fonction numérique
(groupes ciblés : premières toutes séries)

Corrige l'extrait suivant rédigé par un élève :

Une fonction numérique est une application d'un ensemble quelconque dans l'ensemble des nombres réels, noté R.

Corrige l'extrait suivant rédigé par un élève :

Le domaine de définition d'une fonction numérique est un intervalle contenu dans l'ensemble R des
nombres réels.

Corrige l'extrait suivant rédigé par un élève :

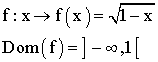
dérivées et primitives
(groupes ciblés : terminales toutes séries confondues)

1- dérivées

On te donne l'expression xⁿ où n est entier naturel différent de 0 et uⁿ, u étant une fonction numérique
de la variable x.

L'erreur souvent commise est d'appliquer la même formule : n.x^n-1dans la recherche des dérivées de xⁿ
et de uⁿ.

Si la dérivée de xⁿ est n.x^n-1, celle de uⁿ est n.u'.u^n-1.

Trouve l'erreur dans le passage suivant et rectifie :

f(x) = 3x⁴ - 5x³ - (x³ - 2x)² implique
f ' (x) = 12x³ - 15x² - 2(x³ - 2x)

2- primitives

Soit f une fonction numérique de la variable réelle x, continue dans son domaine de définition Dom (f).

On note f(x).

Par définition, une primitive F de f est une fonction numérique telle que F'(x) = f(x).

Souvent on oublie que f admet une infinité de primitives qui diffèrent toutes d'une constante réelle.

En effet, soit la fonction g définie par g(x) = F(x) + C, C étant une constante réelle quelconque.
On a g' (x) = F'(x) + 0 = F'(x).
Par conséquent g est une primitive de f.

Trouve l'erreur dans l'énoncé suivant :

f(x) = 2x³ - 3x² .