
L'ATELIER
DU COLLEGIEN
(page 3)
(groupe ciblé : troisième)
les thèmes abordés dans cette page
résolution des équations, de degré supérieur à 1 par rapport à l'inconnue, en utilisant les identités remarquables et par le procédé de factorisation
1- Rappel de cours
Les
identités remarquables souvent utilisées en vue de résoudre des équations
dont le degré est supérieur ou égal 2, sont :

2- Utilisation
des carrés d’une somme et d’une différence
Il
suffit de constater que l’un des membres de l’équation est de la forme :
![]()
Exemples :
![]()
On peut
d’abord mettre 3 en facteur et il vient :
![]()
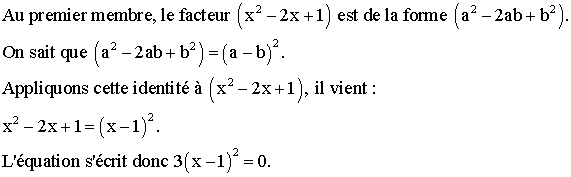
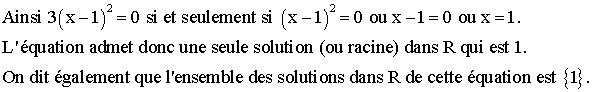
![]()
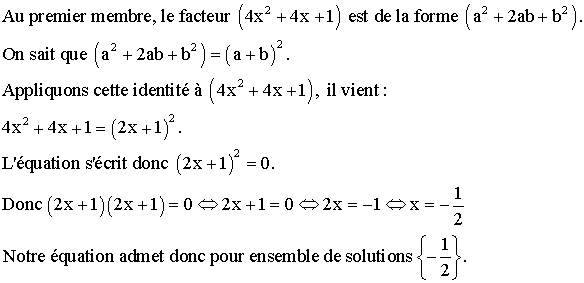
3- Utilisation de la différence de carrés
Il
suffit de constater que l’un des membres de l’équation est de la forme :
![]()
Exemples :
![]()
Rassemblons
tous les termes dans le premier membre ; il vient :
![]()
Le
premier membre est de la forme :
![]()
Nous
avons donc :
![]()
L’équation
s’écrit donc :
![]()
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :

L’équation
admet donc pour ensemble de solutions :
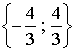
![]()
Rassemblons tous les termes dans le premier membre ; il vient :
![]()
Le
premier membre est de la forme :
![]()
Nous
avons donc :
![]()
L’équation
s’écrit donc :
![]()
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
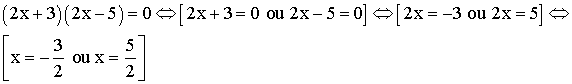
L’équation
admet donc pour ensemble de solutions :
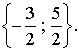
Le premier membre est le carré d’une fraction dont le dénominateur
(y + 1) doit
être différent de 0.
L’équation
n’a donc de sens que si :
![]()
Il faut
donc rechercher les solutions de l’équation dans :
![]()
Rassemblons
tous les termes dans le premier membre ; il vient :

Le
premier membre est de la forme :
![]()
Nous
avons donc :
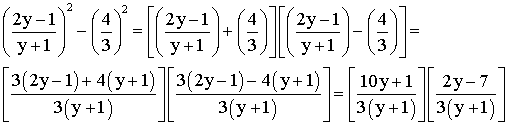
L’équation
s’écrit donc :
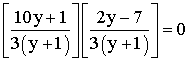
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
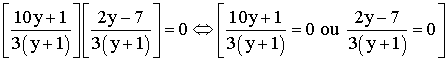
![]()
Le dénominateur
d’une fraction étant différent de 0, cette fraction s’annule lorsque le
numérateur est égal à 0.
Donc,
nous avons :
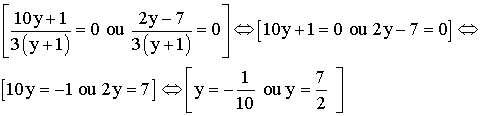
Ces
deux valeurs de y sont toutes deux acceptables car elles sont différentes
L’ensemble des solutions de l’équation est donc :
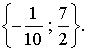
4-
Comment ramener une équation du second degré à une équation dont un
membre est un produit de facteurs contenant au moins un du premier degré
D’abord
une remarque importante :

Soit
maintenant à résoudre l’équation :
![]()
a
étant différent de 0, divisons les deux membres de l’équation par a ;
il vient :
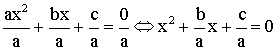
Considérons
maintenant le carré de la somme :
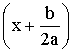
Nous
avons :
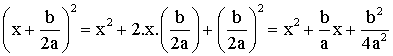

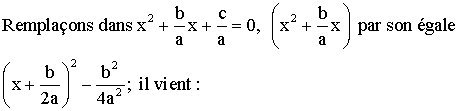

Cette
dernière peut également s’écrire :
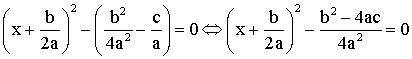
Cette
dernière est donc de la forme :
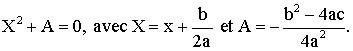
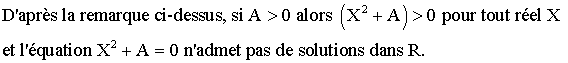
Mais
nous avons :
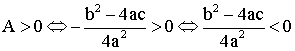

Nous
avons donc :

Ainsi,

Finalement
l’équation s’écrit :
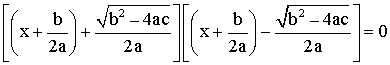
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
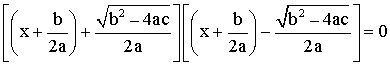
est logiquement équivalent à :

Étudions enfin le cas où A = 0. Nous avons donc :
![]()
L’équation
s’écrit alors :
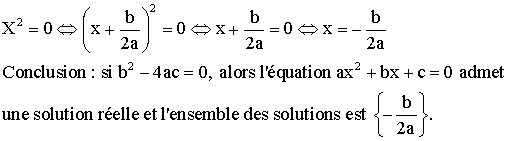
Conclusion
générale :
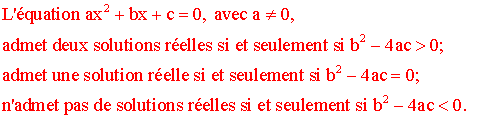
Exemples
![]()
Nous
avons :
![]()
Divisons
les deux membres de l’équation par 3 ; il vient :
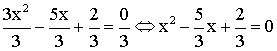
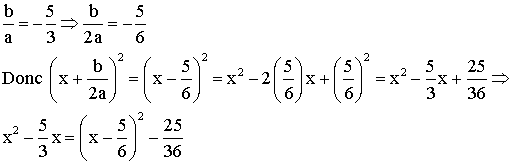
L’équation s’écrit donc :
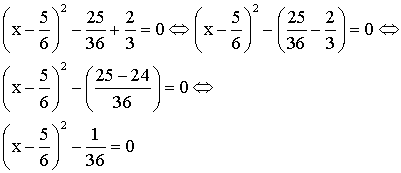
![]()
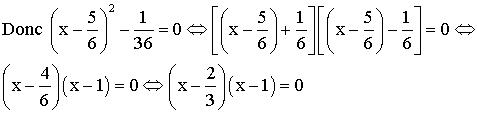
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
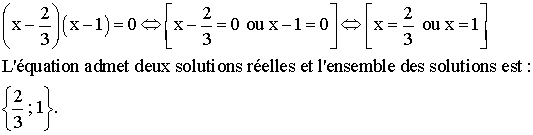
![]()
Nous
avons :
![]()
![]()
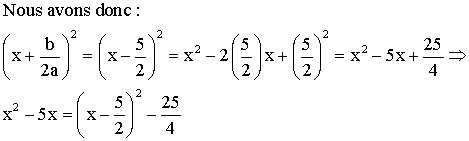
L’équation
s’écrit donc :
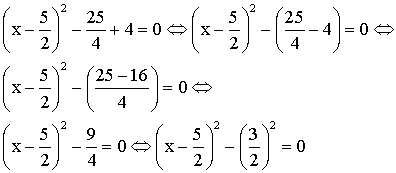
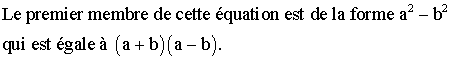
Donc
l’équation s’écrit :
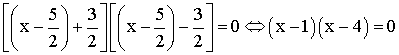
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
![]()
L’ensemble
des solutions dans R de l’équation est donc :
![]()
![]()
Nous avons :
![]()
![]()
Donc nous avons :

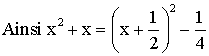
L’équation s’écrit alors :
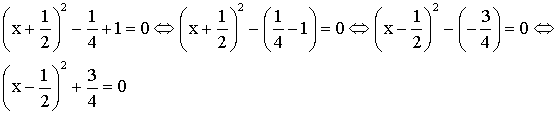
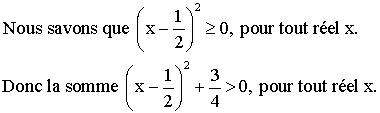
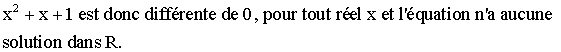
![]()
Il
suffit de constater que :
![]()
ou
![]()
Exemples
![]()
Le
premier membre de l’équation est de la forme :
![]()
Nous
savons que :
![]()
L’équation
s’écrit donc :
![]()
Pour
qu’un produit de facteurs soit nul il faut et il suffit que l’un de ces
facteurs le soit ; donc :
![]()
![]()
Une
des solutions de l’équation est donc 3.
Étudions l’équation :
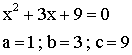
![]()
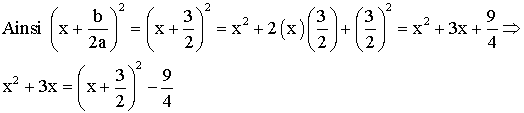
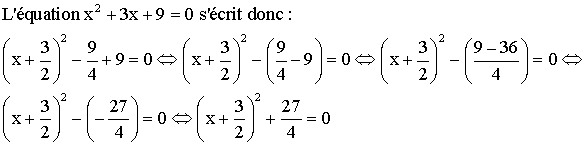
Nous
savons que :
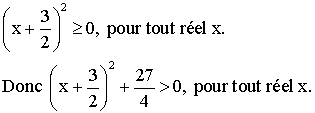
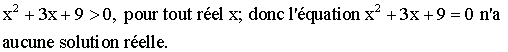
Conclusion :

![]()
Cette
équation peut s’écrire :
![]()
Elle
est donc de la forme :
![]()
Nous
avons donc :
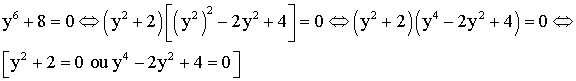
Nous
savons que :
![]()
![]()
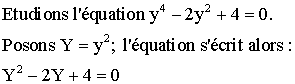
Nous
avons :
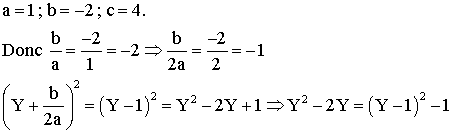
![]()
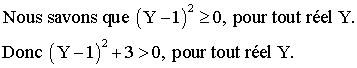
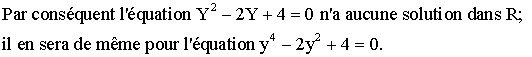
Conclusion :
![]()
![]()
Cette
équation peut s’écrire :
![]()
Elle
est donc de la forme :
![]()
Nous
avons donc :
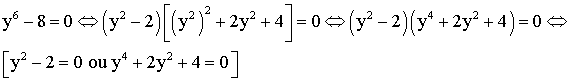
![]()
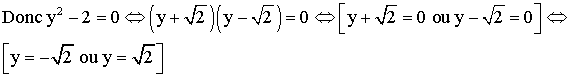
![]()
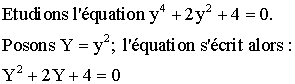
Nous
avons :

![]()
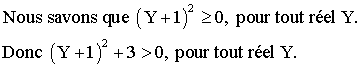
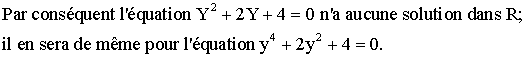
Conclusion :

1- Définition générale d’une transformation ponctuelle
Dans un plan (P) quelconque, une transformation ponctuelle T est une application dans (P).
T applique à tout point M appartenant à (P) un point et un seul M’ appartenant à (P).
M’ sera appelé image de M par la transformation ponctuelle T. On écrit :

On dit aussi que le point M est l’antécédent du point M’ par T.
Si un point M du plan (P)
coïncide avec son image, alors on dira que
M est un point invariant
pour la transformation ponctuelle T.
On a donc :

Une transformation
ponctuelle dans (P), notée Id, est dite
transformation identique si et
seulement si elle rend invariant tout
point de (P).
Dans ce cas, on a :
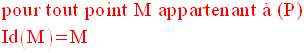
On a également :

2- Composition de deux ou plusieurs transformations ponctuelles
Soient dans un plan (P) deux transformation ponctuelles quelconques T et T’.
On appelle
composée de T suivie de T’, la
transformation ponctuelle, C, dans (P) définie
comme suit :
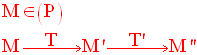
Cette écriture est donc logiquement équivalente à :
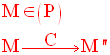
C peut également s’écrire :

Remarque importante : cette dernière écriture se lit « T’ rond T » qui signifie « T suivie de T’ ».
On peut donc lire, comme en langue arabe, de droite à gauche, T suivie de T’.
Propriétés de la composition des transformations ponctuelles
Il est évident que
la composition des transformations n’est pas commutative ;
c’est-à-dire
qu’en général, il existe au moins T et T’ telles
que :
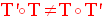
Dans un plan (P), pour
toute transformation ponctuelle T, on a :

S’il existe une et une seule
transformation T’ telle que :

alors on dira que T’ est la transformation ponctuelle symétrique de T par la composition des transformations ponctuelles.
Une transformation T dans un
plan (P) est dite involution ou encore
involutive si et seulement
si elle est identique à sa symétrique par la
composition des transformations ponctuelle ; dans ce
cas on a :
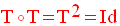
Dans un plan (P), la composition des transformations ponctuelles est associative ; c’est-à-dire :
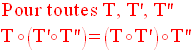
3- Image d’un ensemble de points d’un plan par une transformation ponctuelle
Soit dans un plan (P) une transformation ponctuelle T.
Soit un ensemble E quelconque de points M de (P).
L’ensemble E’ des points images des points M par T est appelé image de E par T ; il est noté :

Un ensemble E de points M de
(P) sera dit invariant point par point,
par T, si et seulement si
tout point M de E est invariant par T.
Un ensemble E de points M de (P) sera dit globalement invariant, par T, si et seulement si :
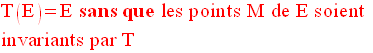
4- Rappel de deux transformations ponctuelles
étudiées dans les classes antérieures
La symétrie centrale
Soit dans un plan (P) un point O quelconque.
On appelle
symétrie centrale de centre O, la transformation
dans (P) , notée SO,
et définie
comme suit :
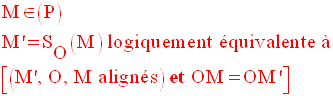
Une autre définition de la symétrie centrale
On peut définir la symétrie centrale à l’aide des vecteurs ; en effet :
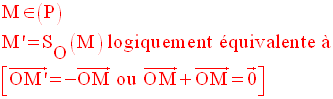
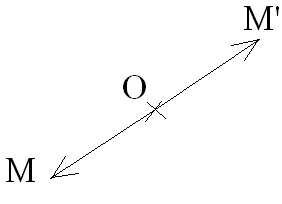
La symétrie centrale dans un plan muni d’un repère

Or,
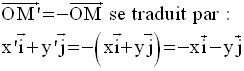
On sait que deux vecteurs
sont égaux (on dit aussi
équipollents) si et seulement si leurs
composantes scalaires de même nom le sont ; ainsi :

Dans la
symétrie centrale dont le centre est l’origine du repère, tout point M a
pour image
le point M’ dont l’abscisse et l’ordonnée sont respectivement les opposées
de celles de M.
Réciproquement,
si deux points M et M’ de ce plan ont leurs abscisses et leurs
ordonnées
respectivement opposées, alors ils sont symétriques dans la
symétrie centrale dont le centre
est l’origine du repère.
Conclusion
Pour que deux
points du plan soient symétriques par rapport à l’origine du repère,
il faut et
il suffit que leurs abscisses et leurs ordonnées soient
opposées.
De cette conclusion, on peut déduire la propriété suivante :

Cette propriété permet de
dire que d’une manière générale, l’image d’un vecteur
par une symétrie
centrale est un vecteur qui lui est opposé.
Propriétés de la symétrie centrale
Le seul point du plan (P) invariant par la symétrie centrale de centre O est le point O.
Toute droite du plan (P) passant par le centre O de la symétrie centrale est
globalement
invariante par cette symétrie centrale.
Démonstration
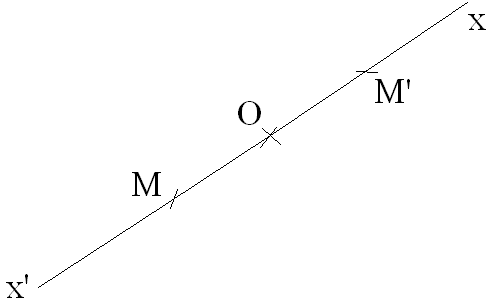
La droite (x’x) passe par O.
Tout point M de la
demi-droite [Ox’), différent de O, a pour
symétrique le point M’ de la
demi-droite [Ox), tel que :
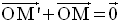
Ces points M ne sont pas invariants par cette symétrie.
Cependant, l’image de [Ox)
est [Ox’) et réciproquement ; donc la droite (x’x), union de ces
deux demi-droites, est globalement invariante par cette
symétrie.
La symétrie centrale est une involution.
Démonstration
Dans le plan (P), soit une symétrie centrale quelconque SO, de centre O.
Soit M un point quelconque appartenant à (P).
Soient :
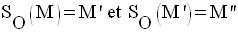
On a donc :

Par conséquent,
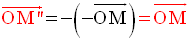
Donc, M’’et M sont confondus et par conséquent,
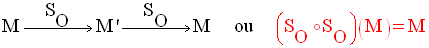
Donc,
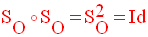
La symétrie
centrale conserve l’alignement de points :
si trois points sont alignés, alors leurs
images le sont également.
Toute droite du
plan ne passant pas par le centre d’une symétrie centrale
a pour image
une
droite qui lui est parallèle.
On en déduit que
la symétrie centrale conserve le parallélisme : deux droites
parallèles ont
pour images deux droites parallèles.
La symétrie
centrale conserve l’orthogonalité de deux droites : deux droites perpendiculaires
ont pour images deux droites perpendiculaires.
La symétrie centrale conserve les distances.
La symétrie
centrale conserve les milieux de segments :
si S est un segment de milieu M,
alors son image S’est un segment
de milieu M’, M’étant l’image de M.
La symétrie centrale conserve les angles.
La symétrie centrale conserve les aires.
La symétrie
centrale conserve les propriétés géométriques d’une figure.
L’image d’un carré est un carré de même
dimension ; l’image d’un rectangle est un rectangle
de mêmes dimensions, l’image d’un triangle est un triangle de mêmes périmètre et
aire ; l’image
d’un polygone quelconque est un polygone de mêmes périmètre et aire.
Un triangle quelconque ayant pour orthocentre,
centre du cercle qui lui est inscrit, centre du
cercle qui lui est circonscrit et centre de gravité, respectivement les points
H, I, J et G, a pour
image par une symétrie centrale quelconque, un
triangle dont l’orthocentre, le centre du cercle
qui lui est inscrit, le centre du cercle qui lui est circonscrit et le centre de
gravité, sont les
symétriques H’, I’, J’ et G’ des points H, I, J et G.
Un cercle
quelconque de centre P et de rayon r a pour image
par une symétrie centrale
quelconque un cercle de centre P’,
image de P par cette symétrie et pour rayon r.
Un cas particulier : si un
cercle a son centre confondu avec le centre d’une
symétrie centrale,
alors il est globalement invariant par cette
symétrie.
La symétrie axiale
Soit dans un plan (P) une droite d quelconque.
On appelle
symétrie axiale d’axe d, la transformation dans
(P) , notée Sd,
et définie
comme suit :

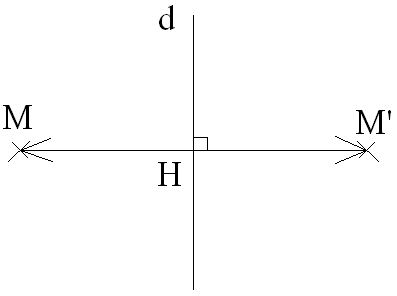
D est donc médiatrice du
segment [MM’] : l’axe de symétrie est médiatrice du
segment obtenu
en joignant un point à son image.
La symétrie axiale dans un plan muni d’un repère orthogonal


Par conséquent, (MM’)
parallèle à l’axe des abscisses ; donc, les ordonnées de
M, M’
et H sont égales.
Ainsi,
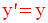
De plus,
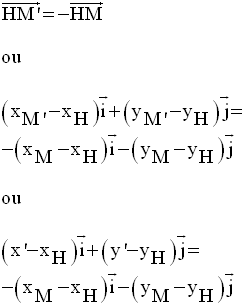
Or, H appartient à l’axe des ordonnées ; donc son abscisse est nulle et ainsi :
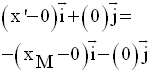
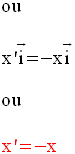
Dans la
symétrie axiale d’axe, l’axe des ordonnées du repère orthogonal, tout
point M a pour
image le point M’ dont l’abscisse est l’opposée de celle de M et
l’ordonnée est égale à celle
de M.
Réciproquement,
si deux points M et M’ de ce plan ont leurs abscisses opposées et leurs
ordonnées égales, alors ils sont symétriques dans la symétrie axiale,
d’axe, l’axe des ordonnées
du repère orthogonal.
Conclusion
Pour que deux
points du plan soient symétriques par rapport à l’axe des ordonnées du repère
orthogonal, il faut et il suffit que leurs abscisses soient
opposées et leurs ordonnées égales.
On peut de la même façon établir les mêmes propriétés pour la symétrie axiale,
d’axe, l’axe
des abscisses d’un repère orthogonal.
Dans la
symétrie axiale d’axe, l’axe des abscisses du repère orthogonal, tout
point M a pour
image le point M’ dont l’ordonnée est l’opposée de celle de M et
l’abscisse est égale à celle
de M.
Réciproquement,
si deux points M et M’ de ce plan ont leurs ordonnées opposées et leurs
abscisses égales, alors ils sont symétriques dans la symétrie axiale,
d’axe, l’axe des abscisses
du repère orthogonal.
Conclusion
Pour que deux
points du plan soient symétriques par rapport à l’axe des abscisses du repère
orthogonal, il faut et il suffit que leurs ordonnées soient
opposées et leurs abscisses égales.
De ces conclusions, on peut déduire la propriété suivante :

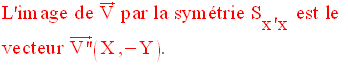
Propriétés de la symétrie axiale
Dans un plan, l’ensemble des points invariants par une symétrie axiale d’axe d est d.
En effet, tout point appartenant à d est confondu avec son image par cette symétrie.
De plus, d est invariante, point par point, par cette symétrie.
Toute droite du plan
rencontrant l’axe d de cette symétrie en
un point I a pour image, par
cette symétrie, une droite rencontrant d au point I.
Toute droite D du plan
parallèle à l’axe d de cette symétrie a pour image, par cette symétrie,
une droite parallèle à D et d.
Toute droite du plan perpendiculaire à l’axe d de cette
symétrie est globalement invariante
par cette symétrie.
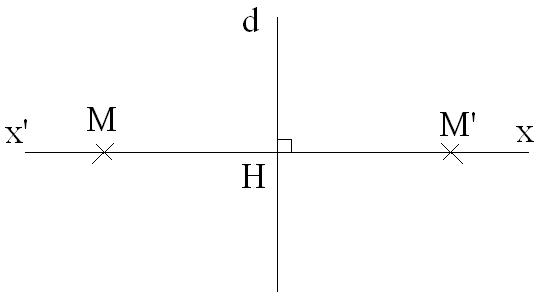
Démonstration
Tout point M de la
demi-droite [Hx’), différent de H, a pour
symétrique le point M’ de la
demi-droite [Ox), tel que :
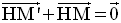
Ces points M ne sont pas invariants par cette symétrie.
Cependant, l’image de [Hx)
est [Hx’) et réciproquement ; donc la droite (x’x), union de
ces deux demi-droites, est globalement invariante par
cette symétrie.
La symétrie axiale est une involution.
La démonstration de cette
propriété est facile ; la méthode est identique à celle utilisée
pour la symétrie centrale.
La symétrie axiale conserve l’alignement de points.
La symétrie axiale conserve le
parallélisme : deux droites parallèles ont
pour images deux
droites parallèles.
La symétrie axiale
conserve l’orthogonalité de deux droites : deux droites perpendiculaires
ont pour images deux droites perpendiculaires.
La symétrie axiale conserve les distances.
La symétrie axiale conserve les milieux de segments.
La symétrie axiale conserve les angles.
On verra au lycée qu’elle ne conserve pas leur orientation ou sens.
La symétrie axiale conserve les aires.
La symétrie axiale conserve les propriétés géométriques d’une figure.
L’image d’un carré est un
carré de même dimension ; l’image d’un rectangle est un
rectangle de mêmes dimensions, l’image d’un triangle est un triangle de mêmes
périmètre
et aire ; l’image d’un polygone quelconque est un
polygone de mêmes périmètre et aire.
Un triangle
quelconque ayant pour orthocentre, centre du
cercle qui lui est inscrit, centre du
cercle qui lui est circonscrit et centre de gravité, respectivement les points
H, I, J et G, a pour
image par une symétrie axiale
quelconque, un triangle
dont l’orthocentre, le centre du cercle
qui lui est inscrit, le centre du cercle qui lui est circonscrit et le centre de
gravité, sont
les symétriques H’, I’, J’ et G’ des points H, I, J et G.
Un cercle
quelconque de centre P et de rayon r a pour image
par une symétrie axiale
quelconque un cercle de centre P’,
image de P par cette symétrie et pour rayon r.
Un cas particulier : si un
cercle a son centre appartenant à l’axe de la symétrie
axiale,
alors il est globalement invariant par cette
symétrie.
4- La translation
4-1 Définition
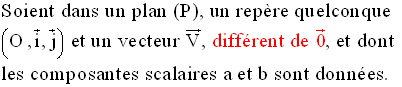

On a donc :

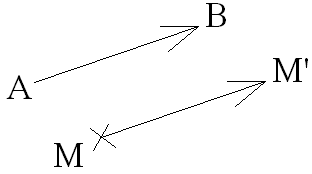
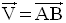
Si x, y sont les coordonnées
de M dans ce repère et si x’, y’ sont celles de l’image M’
dans ce même repère, alors on a :
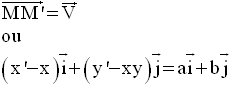
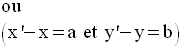
Donc, on en déduit :

Ce sont les relations qui
donnent les coordonnées de l’image M’, en fonction de
celles du
point M, dans cette translation.
La translation de vecteur nul est égale à la transformation identique.
4-2 Propriétés de la translation
La translation n’est pas involutive.
La composée de deux translations est
une translation.
Démonstration
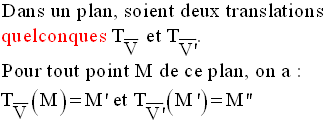
Or,
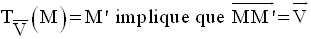
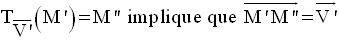
L’addition vectorielle donne :
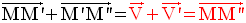
Par conséquent :
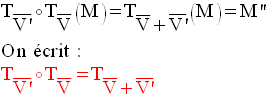
La composée de
deux translations est une translation de vecteur la somme vectorielle
de leurs vecteurs.

Démonstration
On a :

On dit aussi que deux translations symétriques ont leurs vecteurs opposés.
La translation n’admet aucun point invariant.
Toute droite du
plan, parallèle à la direction du vecteur qui définit la translation est
globalement
invariante par cette translation.
Démonstration
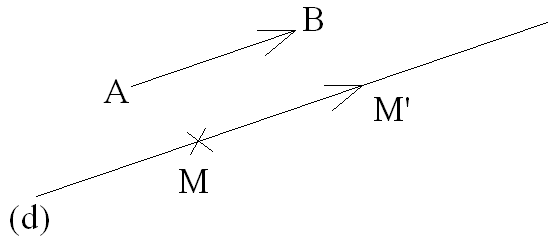
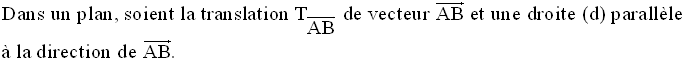
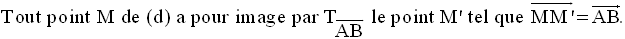
Donc, (MM’) est parallèle à (AB) ; Or, par M ne passe qu’une seule droite, (d), parallèle à (AB).
par conséquent, M’ appartient à (d).
Pour tout point M de (d) a
donc son image appartenant à (d) ; (d) est ainsi
globalement invariante
par la translation donnée.
L’image d’une
droite non parallèle à la direction du vecteur qui définit la translation
est une
droite qui lui est parallèle.
Démonstration
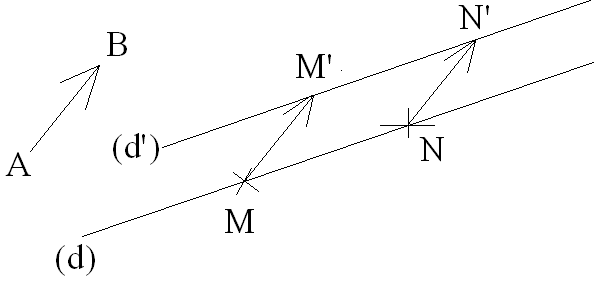
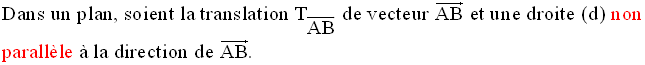
Soient deux points M et N distincts appartenant à (d).
On a :
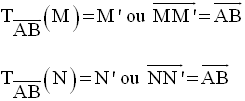
Par conséquent,
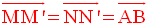
Ce qui implique que le quadrilatère (MM’N’N) est un parallélogramme.
Donc, les droites (MN) = (d) et (M’N’), image de (d) par cette translation, sont parallèles.
La translation conserve l’alignement de points.
La translation
conserve le parallélisme : deux droites
parallèles ont pour images deux
droites parallèles.
A titre d’exercice, je te laisse démontrer cette propriété.
La translation conserve l’orthogonalité de deux droites : deux droites perpendiculaires ont pour images deux droites perpendiculaires.
A titre d’exercice, je te laisse démontrer cette propriété.
La translation conserve les distances.
A titre d’exercice, je te laisse démontrer cette propriété.
La translation conserve les milieux de segments.
La translation conserve les angles.
A titre d’exercice, je te laisse démontrer cette propriété.
La translation conserve les aires.
A titre d’exercice, je te laisse démontrer cette propriété.
La translation conserve les propriétés géométriques d’une figure.
L’image d’un carré est un
carré de même dimension ; l’image d’un rectangle est un rectangle
de mêmes dimensions, l’image d’un triangle est un triangle de mêmes périmètre et
aire ; l’image
d’un polygone quelconque est un polygone de mêmes périmètre et aire.
De plus, les côtés homologues dans cette translation ont leurs directions parallèles.
Un cercle
quelconque de centre P et de rayon r a pour image
par une translation un cercle de
centre P’, image de P par cette translation et
pour rayon r.
La composée de deux symétries centrales de centres différents est une translation.
Démonstration
Soient dans un plan deux symétries centrales SO, SO’ de centres O et O’.
Soit M un point quelconque de ce plan distinct de O et de O’.
On a :
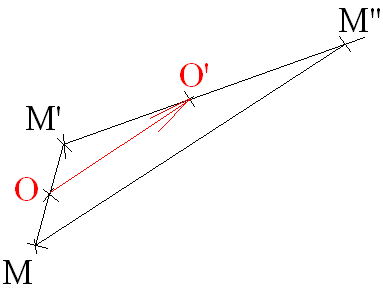
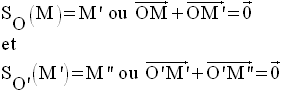
De plus on a l’égalité vectorielle :

Or, les propriétés de la symétrie centrale donnent :
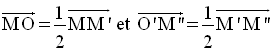
Donc,

Finalement,

On écrit :
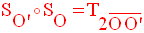
Dans un plan, la
composée SO’ ○ SO, de deux symétries centrales SO
et SO’ de centres
respectifs O et O’, distincts, est égale à la translation de vecteur :

A titre d’exercice, je te laisse démontrer que :

Dans le plan, la composée de deux symétries axiales d’axes parallèles d et d’ est une translation.
Si la distance de
d à d’ est égale à a, alors le vecteur de cette translation a pour longueur
géométrique (on dit aussi module) égale à 2a.
Démonstration
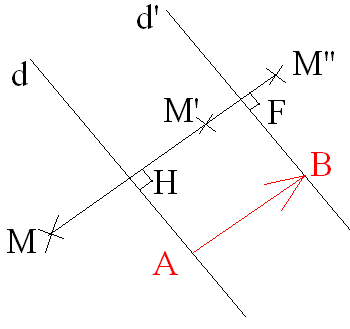
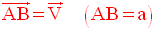
[AB] est le segment porté
par la perpendiculaire commune à d et d’ ; la
distance de d à d’
est donc AB égale a.
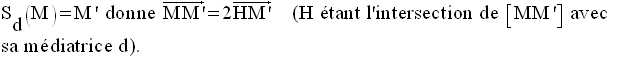
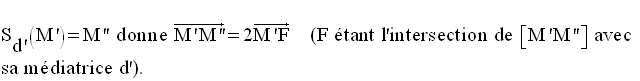
Or,
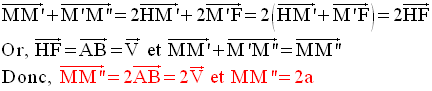
On écrit :
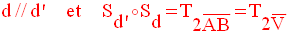
A titre d’exercice, démontre que :
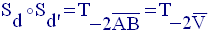
5- La rotation
5-1 Définition
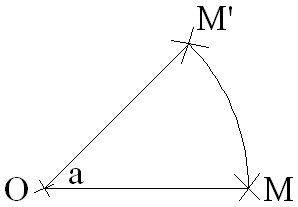
Soit dans un plan (P) un point O quelconque.
On appelle rotation de centre O et d’angle de mesure a, a étant donnée en degrés, la transformation ponctuelle, notée Rot(O,a), appliquant à un point M différent de O, quelconque, appartenant à (P), l’unique image, le point M’ de (P) tel que :

5-2 Propriétés d’une
rotation
Soit dans un plan une
rotation quelconque Rot(O,a), l’angle de
rotation, de mesure a, étant
balayé dans le sens
contraire des aiguilles d’une montre.
L’image d’une droite par cette rotation est une droite.
L’image d’une
droite quelconque passant par le centre de rotation O est une droite passant
par
ce centre.
Rot(O,a) conserve l’alignement de points.
Rot(O,a)
conserve le parallélisme et l’orthogonalité : si deux droites sont parallèles
(ou perpendiculaires), alors leurs images sont parallèles (ou perpendiculaires).
Rot(O,a) conserve les angles.
Rot(O,a) conserve les distances.
Rot(O,a) conserve les milieux de segments.
Rot(O,a)
conserve les propriétés d’une figure géométrique :
l’image d’un polygone quelconque
est un polygone
de mêmes périmètre et aire.
Si un cercle du
plan a pour centre, le centre O de RotO,a), et si a est différente de 360°,
alors ce cercle est globalement invariant par cette rotation.
Si a est égale à 360°, alors ce cercle est invariant point par point.
Dans un plan,
la composée de deux rotations Rot(O,a) et Rot(O,b), de même centre O est
une
rotation de centre O et d’angle égal à la somme des angles a et b. De plus,
la composition des
rotations de même centre est commutative.
On écrit :
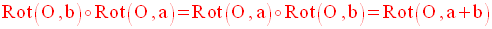
On en déduit un cas
particulier : a et b sont supplémentaires
Dans ce cas, la composée se réduit à la symétrie
centrale SO.
Dans un plan,
la composée Sd’ ○ Sd de deux symétries axiales d’axes les
deux droites d et d’ concourantes au point O, d et d’ formant un angle aigu
mesurant a, a étant balayé dans le sens
contraire des aiguilles d’une montre, est égale à la rotation Rot(O,2a).
Démonstration
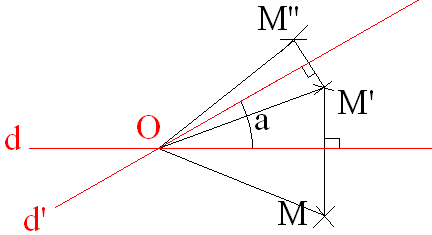
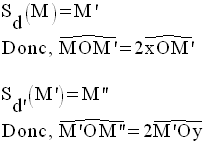
Or,
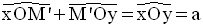
Par conséquent,
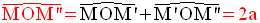
Par ailleurs, OM et OM’’ sont égales.
Par conséquent, la composée Sd’ ○ Sd est égale à Rot(O,2a).
Cas particulier : a est égale à 90°
Dans ce cas, la composée se réduit à la symétrie centrale SO.
Exercices
1)
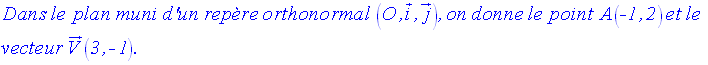
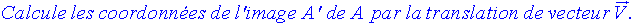
Solution
On sait que :
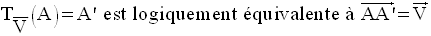
Donc,
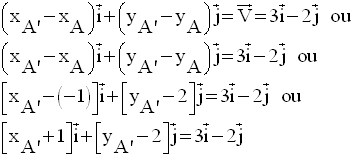
Deux vecteurs sont égaux (on
dit aussi équipollents) si et seulement si leurs composantes
scalaires de même nom sont égales ; donc :
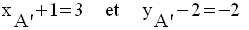
Ces deux égalités impliquent :
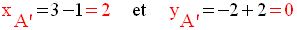
2)

Solution
On sait que la symétrie
centrale de centre O, origine du repère, transforme un point M(x,y)
en un point M’(– x , – y).
En posant SO, on obtient :
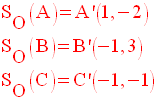
On sait que la symétrie
axiale d’axe, l’axe des abscisses, transforme un point M(x,y)
en un
point M’(x , – y).
En posant Sx’x, on obtient :
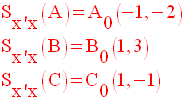
On sait que la symétrie
axiale d’axe, l’axe des ordonnées, transforme un point M(x,y)
en un
point M’(– x , y).
En posant Sy’y, on obtient :
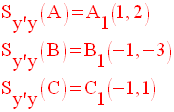
3)
Dans le plan, on donne un triangle quelconque (ABC).
Soit A’ le symétrique de A par rapport à la droite (BC).
Démontre que l’aire du triangle (A’BC) est égale à celle du triangle (ABC).
Solution
Les triangles (ABC) et (A’BC) sont symétriques dans la symétrie axiale d’axe (BC).
Or,
on sait que la symétrie axiale conserve les aires,
donc les triangles (ABC) et (A’BC)
ont même aire.
4)
Dans le
plan, on donne le parallélogramme (ABCD) de centre O (O est donc l’intersection
de ses diagonales).
a-
Démontre que les triangles (ABD) et (CDB) ont même aire. Que peux-tu en conclure ?
b-
D’un point
quelconque K appartenant à (BD), on mène une droite parallèle à (AB) qui
rencontre (BC) et (AD) respectivement en G et H.
Toujours de
K, on mène une droite parallèle à (BC) qui rencontre (AB) et (DC)
respectivement en E et F.
Démontre que les aires des parallélogrammes (KGCF) et (AEKH) sont égales.
Solution
a-
Soit SO la symétrie centrale de centre O.
On sait que dans un parallélogramme, l’intersection des diagonales est le milieu de ces dernières.
Par conséquent :
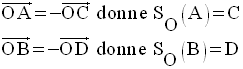
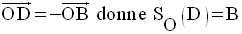
Ainsi,
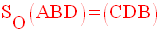
Or, on sait que
la symétrie centrale conserve les aires ; donc
les triangles (ABD) et (CDB),
étant symétriques dans la symétrie centrale SO, ont
même aire.
Conclusion :
une diagonale d’un parallélogramme partage ce dernier en deux triangles de même
aire.
b-
Pour simplifier les écritures, l’aire d’une figure F se notera :
a(F).
D’après la conclusion ci-dessus, on a :
[BD] étant une diagonale du parallélogramme (ABCD), a(ABD) est égale à a(BCD)
[BK] étant une diagonale du parallélogramme (EBGK), a(EBK) est égale à a(BGK)
[KD] étant une diagonale du parallélogramme (KFDH), a(KHD) est égale à a(KFD)
Or, on a :
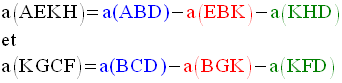
Deux quantités égales à une
même troisième sont égales ; donc les parallélogrammes (AEKH)
et (KGCF) ont même aire.
5)

Solution
Il s’agit là d’une construction géométrique.
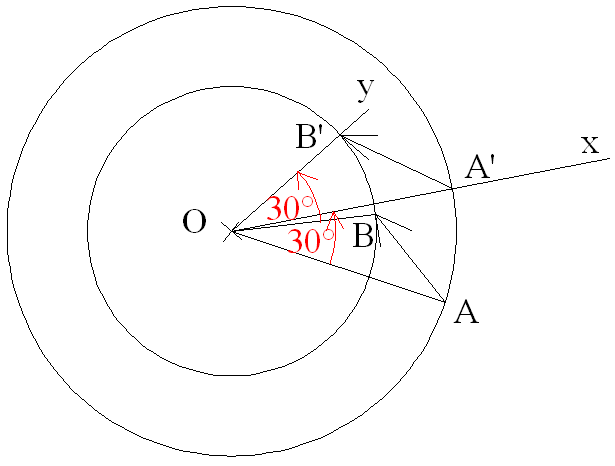
Si A’ est l’image de A par la rotation Rot(O,30°), alors :
Je trace donc le cercle de centre O et de rayon OA.
Le point A’
sera l’intersection de ce cercle et de la demi-droite [Ox) faisant avec [OA)
un angle balayé dans le sens contraire des aiguilles d’une montre et égal à 30°.
Si B’ est l’image de B par la rotation Rot(O,30°), alors :
Je trace donc le cercle de centre O et de rayon OB.
Le point B’
sera l’intersection de ce cercle et de la demi-droite [Oy) faisant avec [OB)
un angle balayé dans le sens contraire des aiguilles d’une montre et égal à 30°.
6)

Solution
On sait que la pente 2 de
la droite d est la tangente de l’angle aigu que forme d avec
l’axe des abscisses.
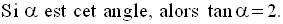
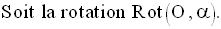
L’image du support (x’x) de
l’axe des abscisses par cette rotation est donc la droite D passant
par O et de pente 2.

7)

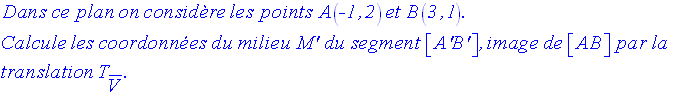
Solution
La méthode : on calcule
d’abord les coordonnées des images A’ et B’ de A et B par la
translation donnée ; puis on applique les formules donnant les coordonnées de M’
milieu
de [A’B’].
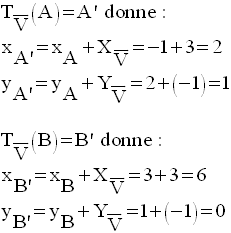
On sait que si M’(x’,y’) est milieu de [A’B’], alors :
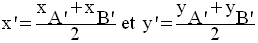
Donc,
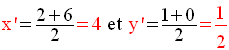
8)
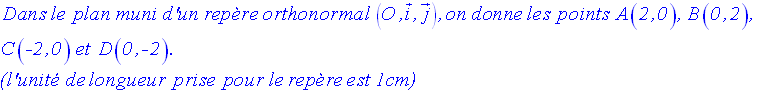

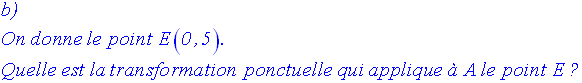

Solution
Dans le repère donné, on place les points A, B, C, D, E et F.
a)
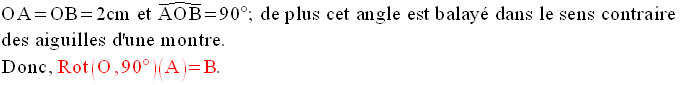
Il en sera de même pour les deux autres questions de 1) ; je te laisse donc démontrer que l’on a :

b)
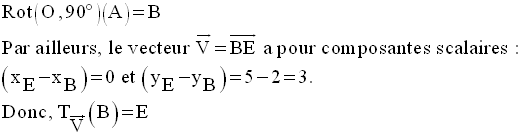

c)

Par ailleurs, on a :
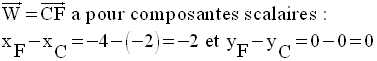
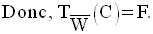
Finalement, on obtient :
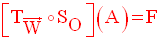
9)

Solution
Soit :
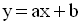
l’équation de d’.
La translation transformant
une droite en une droite qui lui est parallèle,
la pente de d’ devra
donc être égale à celle de d.
L’équation de d’ prend la forme :
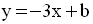
d rencontre l’axe des ordonnées au point B(0,– 1).
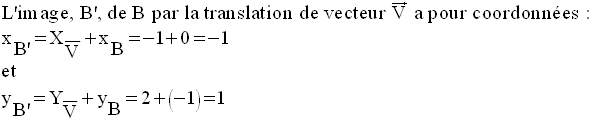
Or, B’ appartient à d’ ; ces coordonnées vérifient l’équation de d’.
On a donc :
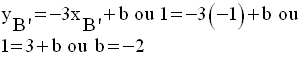
L’équation de d’ est finalement :
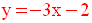
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)