(groupes ciblés : première et terminale S)
les thèmes abordés dans cette page
géométrie vectorielle - barycentre d'un système
de points pondérés
(1ère S)
fonctions
numériques dérivables en un point
(1ère et terminale S)
les
asymptotes
(groupe ciblé : première S)
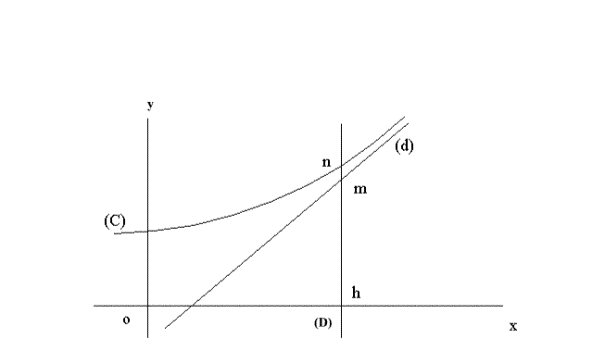
asymptote oblique

(C)
est la courbe représentative de f dans le repère orthonormal (x’ox) ;
La
droite (d) a pour équation y = ax + b
On
considère une droite (D) parallèle à l’axe y’y coupant l’axe (x’x),
(d) et (C) respectivement en h, m et n.
On
considère la quantité algébrique :
![]()
(d)
est asymptote à (C) si et seulement si la limite de cette quantité algébrique
tend vers 0 lorsque x tend
vers + ou – l’infini.
Divisons
cette quantité par x (la division est possible, puisque x tendant vers
l’infini est différent de 0) ; on obtient la
quadruple égalité (1) :
![]()
Formons
l’expression f(x) – ax ; on obtient l'égalité (2) :
![]()
Dans la quadruple égalité (1) ci-dessus, la limite du 1er membre lorsque x tend vers l’infini est 0 ; donc le dernier membre tend également vers 0 ; mais aussi la fraction :
![]()
![]()
Dans
la deuxième égalité (2) ci-dessus, la limite de
[f(x) – (ax + b)] étant 0 lorsque x tend vers l’infini, la limite de [f(x) – ax] lorsque x tend
vers l’infini est b.
Conclusion :
(d) est asymptote à (C) si et seulement si , x tendant vers + ou – l’infini, la limite « a » de l'expression :
![]()
existe et est finie.
ET
la limite « b »
de l'expression :
[f(x) – ax]
existe et est finie.
Exemple : f est définie sur R- {1} par :
![]()
![]()
et on obtient :
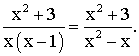
Au numérateur comme au dénominateur, on met la plus grande puissance de x en facteur ; on obtient :
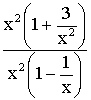
On
peut simplifier par x2 puisque
x tendant vers l’infini est différent de 0 et on obtient :
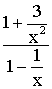
et le passage à la limite donne 1 puisque les deux fractions :
![]()
![]()
Formons
l'expression f(x) – ax ; on a :
![]()
et en mettant au même dénominateur on obtient :
![]()
Au numérateur comme au dénominateur, on met la plus grande puissance de x en facteur ; on obtient :
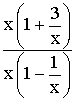
On
peut simplifier par x puisque
x tendant vers l’infini est différent de 0 et on obtient :
![]()
et le passage à la limite donne 1 puisque les deux fractions :
![]()
Ainsi
la limite de [f(x) – x] lorsque x tend vers + ou – l’infini est égale
à 1
Conclusion :
(C) admet une asymptote oblique qui est la droite d’équation y = 1.x +
1 ou
NB
:
1-
Souvent, dans des problèmes, on te demandera d’étudier la position de la
courbe (C) par rapport à son asymptote (au-dessus ou en dessous) ;
dans ce cas, c’est le signe de la quantité :
![]()
qu’il
faudra étudier ; ainsi :
si
[f(x) – (ax + b) ] est strictement positif à l’infini , (C) est au-dessus
de son asymptote,
si
[f(x) – (ax + b) ] est strictement négatif à l’infini , (C) est en
- dessous de son asymptote.
2-
(C) peut dans certains cas de problème couper son asymptote en un point x0
fini de son domaine de définition ; ceci ne change rien au fait que
(C) admet une asymptote car l’existence de cette dernière est étudiée
« à l’infini »
3-
Méthodologie pour la recherche de l’asymptote oblique
On forme d’abord l’expression :
![]()
puis on calcule sa limite lorsque x tend vers l’infini.
Si cette limite a existe et
est finie, alors on poursuit notre
recherche en formant l’expression [f(x) – ax] et en calculant sa limite b
lorsque x tend vers l’infini.
Si également cette limite b existe et
est finie, alors on conclut que (C)
admet pour asymptote oblique la droite d’équation
y = ax + b.
Si
durant cette recherche l’une au moins a et b n’existe pas ou
est égale à l’infini, alors (C) n’admet pas d’asymptote oblique.
Au
voisinage de l’infini,
la courbe (C) sera au-dessus de son asymptote oblique si et seulement
si la quantité f(x) – [ax + b] est strictement positive. Elle
sera en-dessous de son asymptote si et seulement si la
quantité f(x) – [ax + b] est strictement négative.
Asymptote
verticale
On
dira que (C) admet une asymptote verticale d’équation
x = a (a
réel fini), si et seulement si la
limite de f lorsque x tend vers a est égale à
+ ou – l’infini.
Asymptote
horizontale
On
dira que (C) admet une asymptote horizontale d’équation y = b (b réel fini), si et seulement si
la limite de f lorsque x tend vers + ou – l’infini est égale
à b.
NB :
On
a considéré dans tout ce qui précède que f était représentée
graphiquement dans un repère orthonormé ; il faut savoir que
toutes
les conclusions obtenues restent vraies dans un
repère quelconque
géométrie vectorielle - barycentre d'un
système de points pondérés
(groupe ciblé : première S)
1- Rappel de quelques propriétés établies en géométrie dans l’espace
Trois points non alignés quelconques de l’espace définissent un plan. (Figure 1)
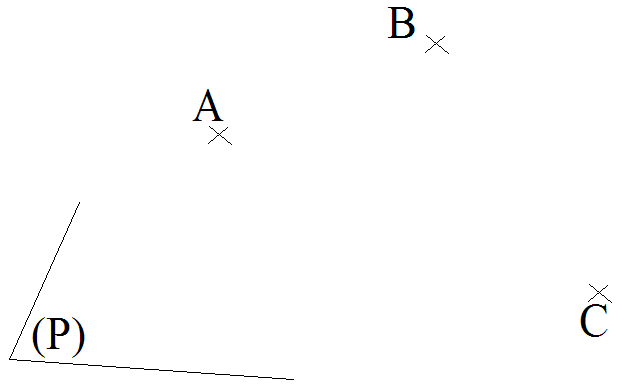
Figure 1 :
les trois points non alignés A, B et C définissent le plan (P).
Chacun de ces trois points appartient au plan (P)
Dans l’espace, la donnée de trois points non alignés quelconques définit un plan.
Une droite
quelconque de l’espace et un point
quelconque de cet espace
n’appartenant
pas à cette droite définissent un plan.
(Figure 2)
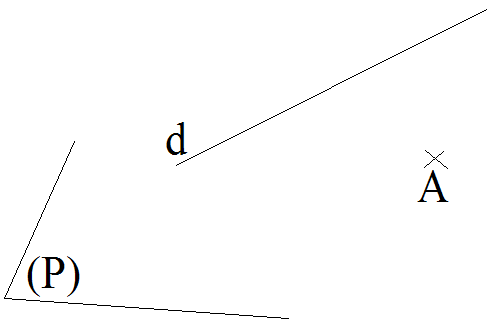
Figure 2 :
La droite d et le point A ne lui appartenant pas définissent le plan (P)
Il suffit de prendre deux points B et C
distincts appartenant à d
et ainsi on est ramené au cas de la figure 1

Dans l’espace,
la donnée d’une droite quelconque et d’un point
quelconque n’appartenant
pas à cette droite définit un plan.
Deux droites concourantes quelconques de l’espace définissent un plan qui les contient. (Figure 3)
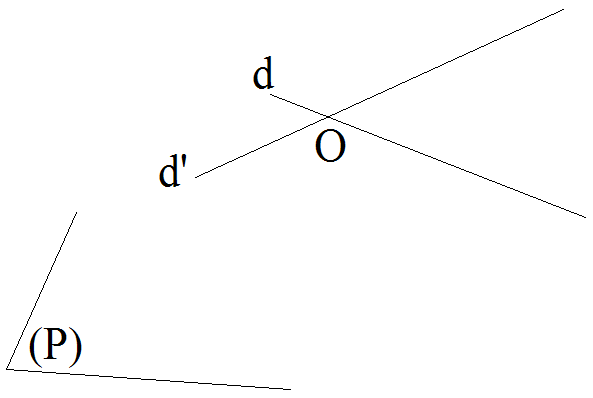
Figure 3 :
d et d’ concourantes au point O définissent le plan (P)
Il suffit de prendre un point A
différent de O et quelconque
appartenant à d et deux points distincts
différents de O et quelconques
appartenant à d’ et ainsi on est ramené au cas de la figure 1
Deux droites de l’espace
sont dites parallèles si elles
appartiennent à un même plan
et si leur intersection est vide.
Remarque importante
Deux droites de l’espace
peuvent avoir une intersection vide tout en
n’étant pas
parallèles.
Dans l’espace, une droite d
non incluse dans un plan P est dite
parallèle à P si son
intersection avec P est vide.
Dans l’espace, une droite d
est parallèle à un plan P si et seulement s’il existe
au moins une droite d’ contenue dans P et
parallèle à d. (Figure 4)
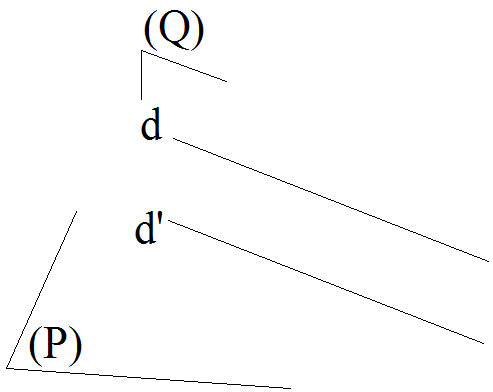
Figure 4
Démonstration
Par hypothèse on a d parallèle à P.
On démontre qu’il existe au moins une droite contenue dans P et parallèle à d.
Soit un plan Q quelconque contenant d et tel que son intersection avec P soit d’.
Si d et d’ étaient
concourantes en un point O, ce point, appartenant à d’, appartiendrait
à P et ainsi il appartiendrait simultanément à d et P ; ce qui contredirait
l’hypothèse.
Conclusion : d et d’ incluses dans Q et non concourantes sont parallèles.
Réciproque
Par hypothèse, on a d’ incluse dans P et parallèle à d.
On démontre que d est parallèle à P.
d et d’ étant parallèles, définissent un plan Q. L’intersection de P et Q est donc d’.
Si d n’était pas parallèle à P, alors il existerait au moins un point O commun à d et P.
O appartenant à d incluse dans Q, appartiendrait à Q.
O appartenant simultanément à Q et P, appartiendrait à leur intersection d’.
Ainsi d et d’ auraient un point commun O ; ce qui contredirait l’hypothèse.
Conclusion : d est parallèle à P
Dans l’espace,
une droite d non contenue dans un plan P est parallèle à
ce plan si et
seulement s’il existe au moins un plan Q contenant d et rencontrant P selon
une
droite d’ parallèle à d. (Figure 5)
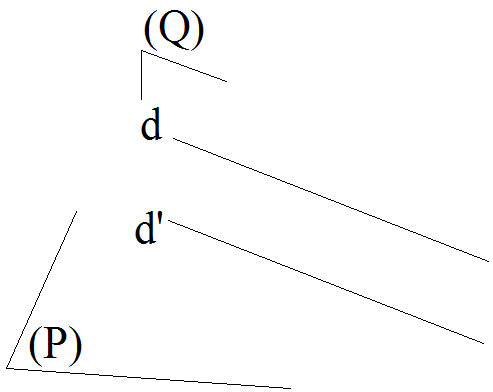
Figure 5
Démonstration
Par hypothèse on a d non contenue dans P et d parallèle à P.
Soit Q un plan quelconque contenant d et sécant à P selon la droite d’.
On démontre que d’ est parallèle à d.
Si d’ et d n’étaient pas parallèles, elles auraient alors au moins un point O en commun.
O appartenant à d’ incluse dans P, appartiendrait à P.
Ainsi, O appartiendrait
simultanément à P et à d ; ce qui contredirait l’hypothèse
qui énonce que d est parallèle à P.
Conclusion : d’ est parallèle à d.
Réciproque
Par hypothèse on
a, d non contenue dans P, Q un plan contenant d et tel que son
intersection avec P est une droite d’ parallèle à d.
On démontre que d est parallèle à P.
Si d et P n’étaient pas parallèles, alors ils auraient au moins un point O en commun.
O appartenant à d incluse dans Q appartiendrait à Q.
O appartenant simultanément à Q et P, appartiendrait à leur intersection d’.
Ainsi, O appartiendrait
simultanément à d et d’ ; ce qui contredirait l’hypothèse qui
énonce que d et d’ sont parallèles.
Conclusion : d est parallèle à P.
Deux plans de l’espace sont dits parallèles si leur intersection est vide.
Dans l’espace, on donne un
plan P quelconque et une droite d parallèle
à ce plan.
Il existe un et un seul plan contenant d
et parallèle à P.
Deux plans de l’espace sont
parallèles, si et
seulement si, l’un, quelconque, de ces
deux plans, contient deux droites concourantes telles
que chacune d’elle est parallèle
à l’autre plan. (Figure 6)
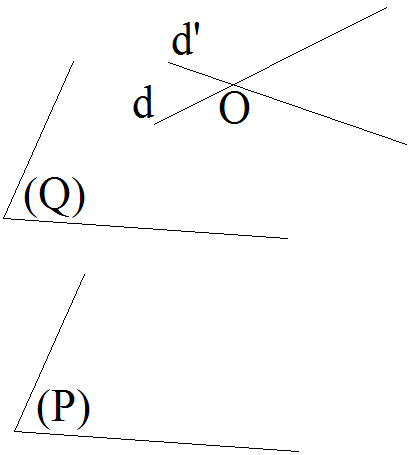
Figure 6 :
d et d’ sont deux droites incluses dans Q,
concourantes, telles que chacune
d’elles est parallèle à P
P et Q sont parallèles
Démonstration
Par hypothèse on a :
P et Q deux plans
parallèles ; d et d’ deux droites concourantes quelconques
incluses dans Q.
On démontre que d et d’ sont parallèles à P.
Si d rencontrait P au point
M, alors M serait commun à P et Q ; ce qui contredirait
l’hypothèse qui énonce que P et Q sont parallèles.
Par conséquent, d est parallèle à P.
Si d’ rencontrait P au point M’, alors M’ serait commun à P et Q ; ce qui contredirait l’hypothèse qui énonce que P et Q sont parallèles.
Par conséquent, d’ est parallèle à P.
Conclusion : d et d’ sont parallèles à P.
Réciproque
Par hypothèse on a :
d et d’ deux
droites concourantes au point O, incluses dans Q, et telles que d est
parallèle à P et d’ parallèle à P.
On démontre que P est Q sont deux plans parallèles.
Si P et Q ne sont pas parallèles, alors il existerait une droite D qui serait leur intersection.
Q contenant la droite d parallèle à P, D serait alors parallèle à d.
Q contenant la droite d’ parallèle à P, D serait alors parallèle à d’.
Dans le plan Q, on aurait
ainsi mené du point O deux droites distinctes d et d’,
parallèles à D ; ce qui contredit l’axiome d’Euclide.
Conclusion : P et Q sont parallèles.
Dans l’espace, un plan
quelconque sécant à des plans
parallèles rencontre ces derniers
selon des droites parallèles. (Figure 7)
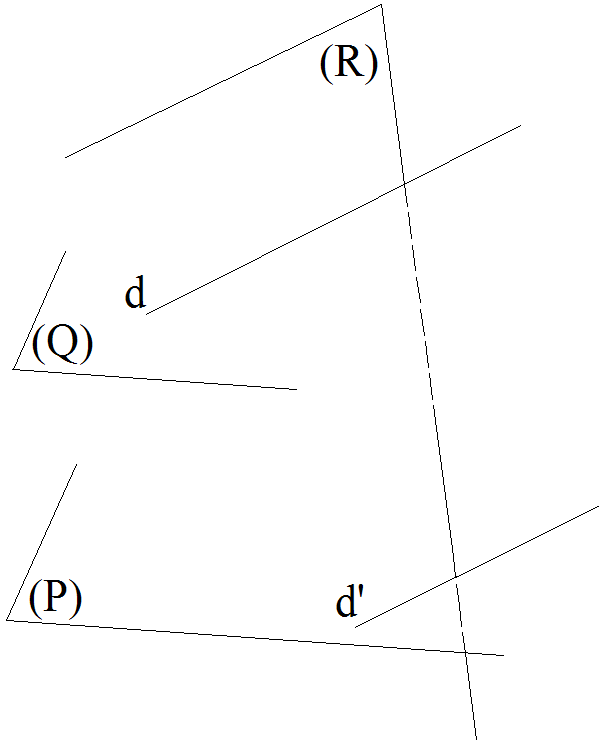
Figure 7 :
P et Q deux plans parallèles
R sécants à P et Q
Par conséquent, d et d’ sont parallèles
Démonstration
On a par hypothèse, deux
plans P et Q parallèles et un plan R sécant à P et à Q,
quelconque.
Soient d’ l’intersection de R et de P et d’ celle de R et Q.
On démontre que d et d’ sont parallèles.
Si d et d’ étaient
concourantes au point M, alors ce point serait commun à P et à Q ;
ce qui contredirait l’hypothèse qui énonce que P et Q sont parallèles.
Conclusion : d et d’ étant incluses dans R et non concourantes sont parallèles.
Construction de sections planes
Soit, dans l’espace, un objet géométrique (F) quelconque.
On appelle
section plane de (F) par un plan qui lui est
sécant l’intersection de (F)
avec ce plan.
Dans des problèmes de
géométrie dans l’espace, souvent la construction des sections
planes d’un objet permet de comprendre
les propriétés géométriques de cet objet
et assure une clarté à la figure.
Exemples de sections planes :
La section plane d’une
sphère par tout plan qui lui est
sécant est un cercle ;
de plus
si ce plan passe par le centre de la sphère,
alors la section plane est un grand cercle
de cette sphère.
La section plane d’un cube
ou d'un parallélépipède rectangle par un plan contenant
deux arêtes symétriques dans la symétrie centrale O,
centre de ce cube ou de ce
parallélépipède rectangle, est un rectangle.
La section plane d'un
parallélépipède quelconque (dit aussi oblique) par un plan
contenant deux arêtes parallèles, est
un parallélogramme.
La section plane d'un
tétraèdre quelconque par un plan parallèle à une
quelconque
des faces de ce tétraèdre est un triangle.
De plus, le théorème de Thalès s'applique
à cette face et ce triangle.
La section plane d’un
tétraèdre régulier par un plan
parallèle à une quelconque des
faces de ce tétraèdre est un triangle équilatéral.
La section plane d’un cône
de base circulaire (C) par un plan parallèle
à cette base
est un cercle.
La section plane d’un cylindre par un plan parallèle à sa base est un cercle.
Pour construire une section
plane d’un objet (F) par un plan P qui lui est sécant,
il faut d’abord avoir une bonne vision dans l’espace.
Il faut repérer des droites coplanaires contenues dans le plan P.
Si ces deux droites sont
concourantes, alors leur point d’intersection est
un point supplémentaire appartenant P, et cette conclusion
facilite, par la suite, la construction
de la section plane à construire.
Exemple :
Sur la figure 8
ci-dessous, (ABCDEFGH) est un cube. M est un point de [BF], N,
un point de [AE] et P, un point de [CD].
On demande de construire la section plane de ce cube par le plan (MNP).
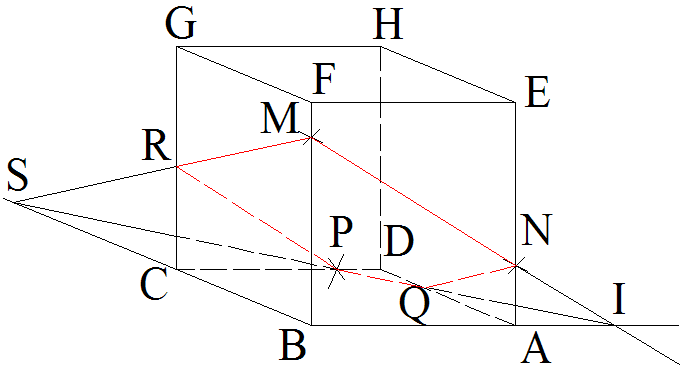
Figure 8
M et N appartenant à (MNP), [MN] est inclus dans (MNP).
[MN],
étant simultanément inclus dans la face (ABFE) et dans (MNP),
est alors
l’intersection de cette face et de (MNP).
(MN) coupe (BA) au point I.
I appartenant à (MN) appartient alors à (MNP).
I et P appartenant à (MNP),
(IP) est alors incluse dans ce plan et Q, intersection de (IP)
et de [AD], appartient à (MNP).
Q et N appartenant à (MNP), [QN] est inclus dans ce plan.
[QN],
étant simultanément inclus dans la face (ADHE) et dans (MNP),
est alors
l’intersection de cette face et de (MNP).
[PQ],
étant simultanément inclus dans la face (ABCD) et dans (MNP),
est alors
l’intersection de cette face et de (MNP).
(IP) rencontre (BC) au point S.
S appartenant à (IP) appartient alors à (MNP).
S et M appartenant à (MNP),
(SM) est alors incluse dans ce plan et R, intersection
de (SM) et [CG], appartient à (MNP).
R et M appartenant à (MNP), [RM] est inclus dans ce plan.
[RM],
étant simultanément inclus dans la face (BCGF) et dans (MNP),
est alors
l’intersection de cette face et de (MNP).
[PR],
étant simultanément inclus dans la face (CDHG) et dans (MNP),
est alors
l’intersection de cette face et de (MNP).
La section du cube (ABCDEFGH) et du plan (MNP) est alors le pentagone (MNQPR).
2- Espace des vecteurs
2-1 Définitions
Un vecteur de l’espace est défini par :
- la droite qui le porte appelée son support ou sa direction
- ses deux extrémités qui définissent sur ce support un segment dont la longueur est appelée module ou longueur géométrique de ce vecteur
-
son sens d’orientation,
de son origine vers son extrémité (cette origine et cette
extrémité étant les extrémités du segment ayant défini le module)
Un vecteur est généralement
noté par une lettre surmontée d’une flèche ou encore
par deux lettres surmontées d’une flèche, la première lettre (de gauche à
droite) étant
l’origine de ce vecteur et la seconde, son extrémité. (Figure 9)
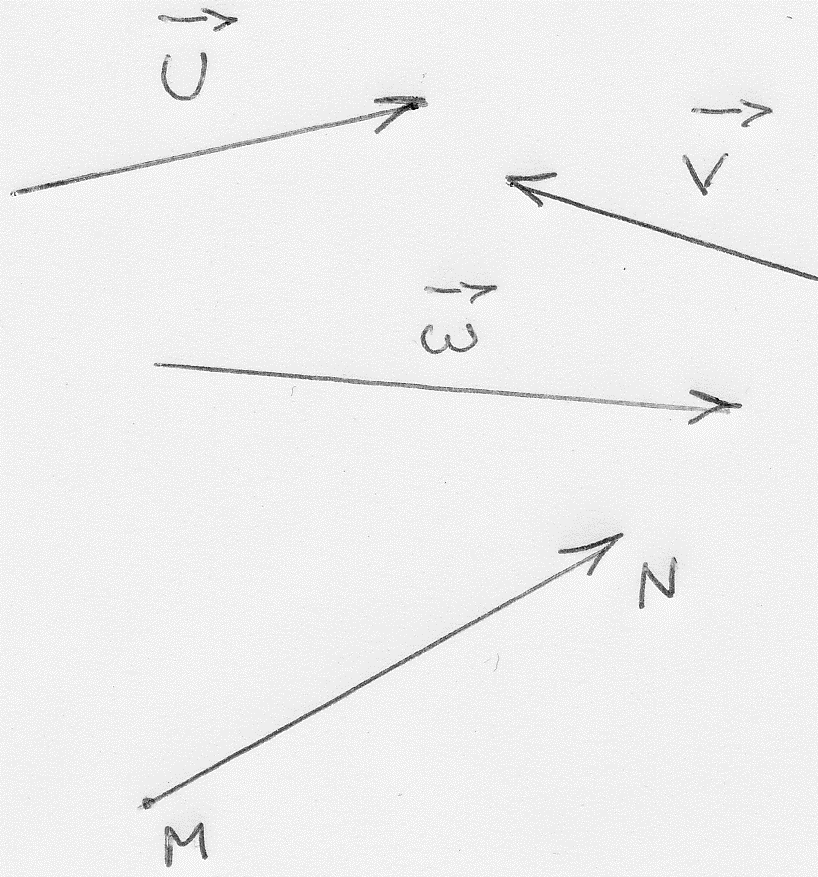
Figure 9
On écrit :
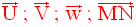
On lit respectivement : « vecteur U ; vecteur V ; vecteur w et vecteur MN ».
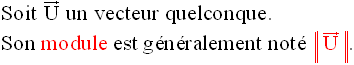
Deux vecteurs sont dits
égaux (ou encore
équipollents) s’ils ont même direction ou
support (ou des directions parallèles), même module et même sens. (Figure
10)
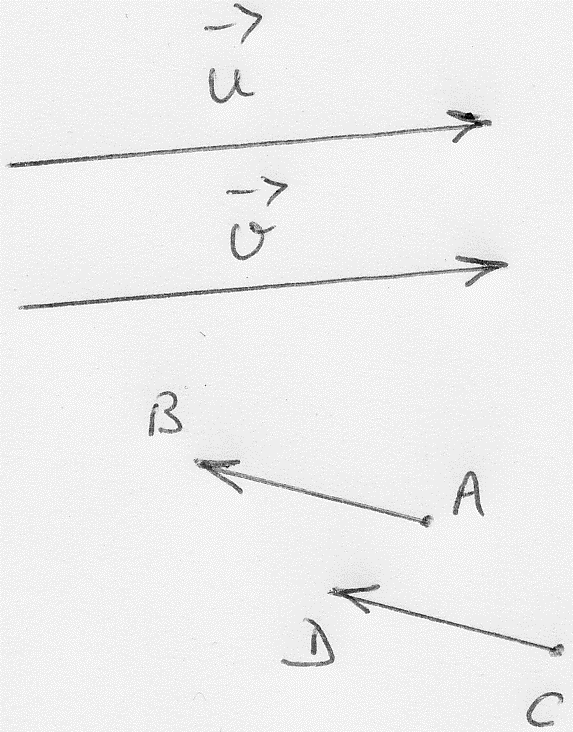
Figure 10 :
On note E l’espace des vecteurs.
On définit dans cet espace une addition, nommée addition vectorielle, ayant les propriétés suivantes :

On définit également dans E
une multiplication d’un nombre réel par un vecteur
de
la manière suivante :
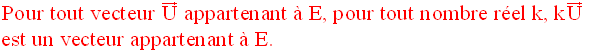

2-2 Relation de Chasles
Soient A, B et C trois points quelconques de l’espace.
On a :
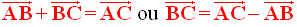
Ce sont les deux écritures de ce qu’on appelle relation de Chasles.
On en déduit immédiatement que :
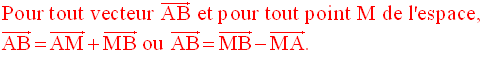

Généralisation de la relation de Chasles
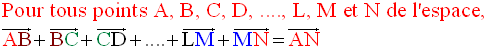
2-3 Construction
géométrique d’une somme et d’une différence de deux
vecteurs donnés

(Figure 11)

Figure 11


(Figure 12)
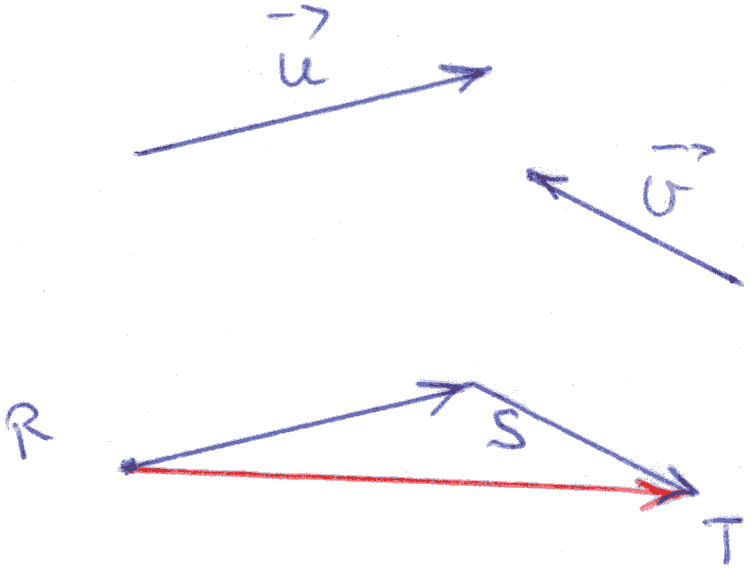
Figure 12

2-4 Construction géométrique d’une somme de plusieurs vecteurs donnés
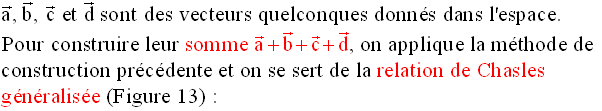
Figure 13

3- Vecteurs colinéaires
3-1 Définition
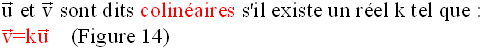

Figure 14
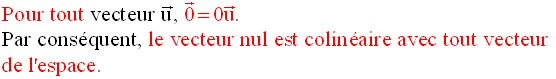
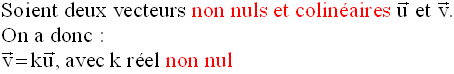

D’où la deuxième définition
de la colinéarité de deux vecteurs non nuls de
l’espace :
deux vecteurs non nuls de l’espace sont dits colinéaires
si leurs directions sont parallèles
ou confondues.


Figure 15
A titre d’exercice, je te laisse démontrer ce théorème.
La démonstration
comporte deux parties : on démontre la condition
nécessaire et
celle suffisante.
4- Combinaison linéaire de deux vecteurs - Vecteurs coplanaires
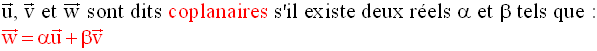

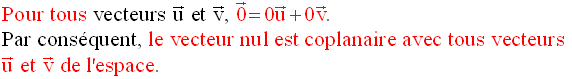
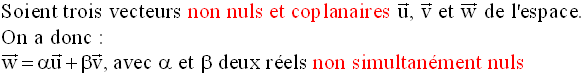
La coplanarité de ces trois vecteurs se caractérise par la propriété suivante :
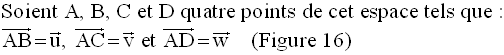
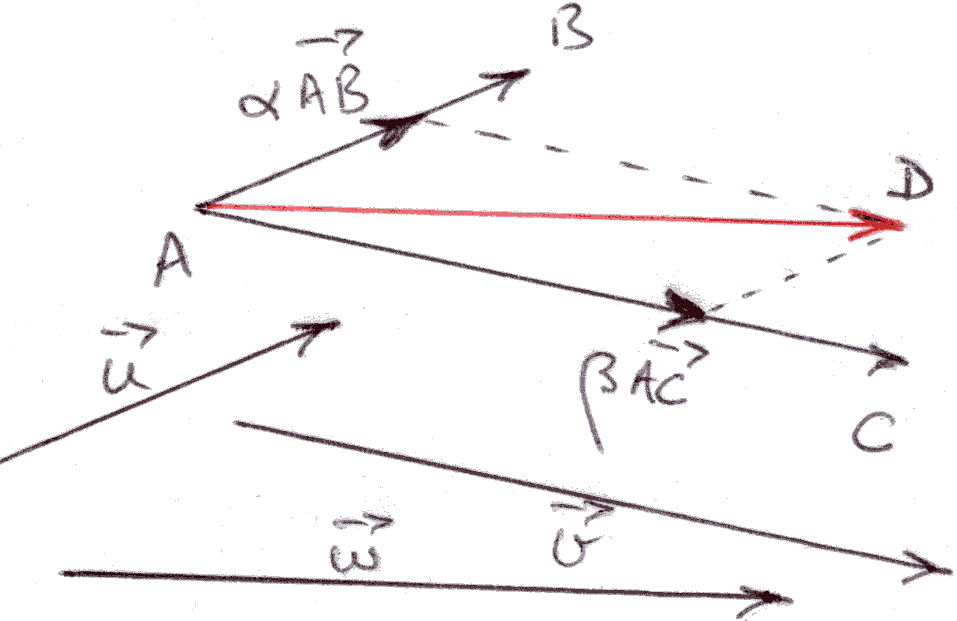
Figure 16


A titre d’exercice, je te laisse démontrer ce théorème.
La démonstration
comporte deux parties : on démontre la condition
nécessaire et
celle suffisante.
5- Caractérisation d’une droite et d’un plan de l’espace
5-1 Caractérisation d’une droite

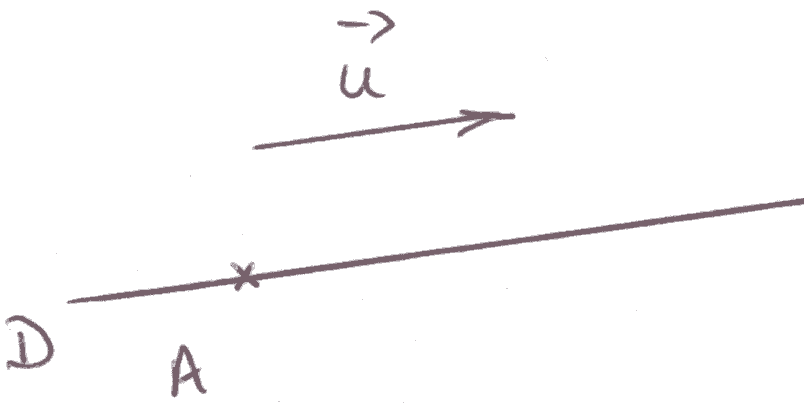
Figure 17

Il est facile d’établir les théorèmes suivants :

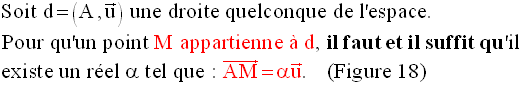

Figure 18
5-2 Caractérisation d’un plan


Figure 19
Il est facile d'établir le théorème suivant :

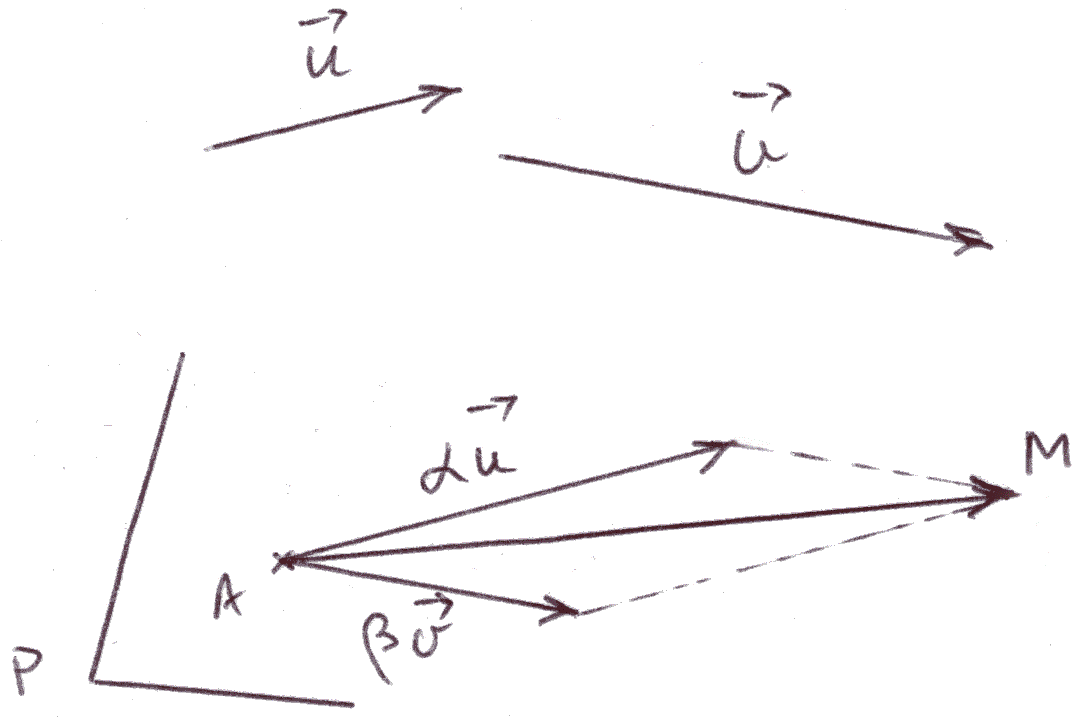
Figure 20
6- Caractérisation de droites et plans parallèles
Théorème
Démonstration
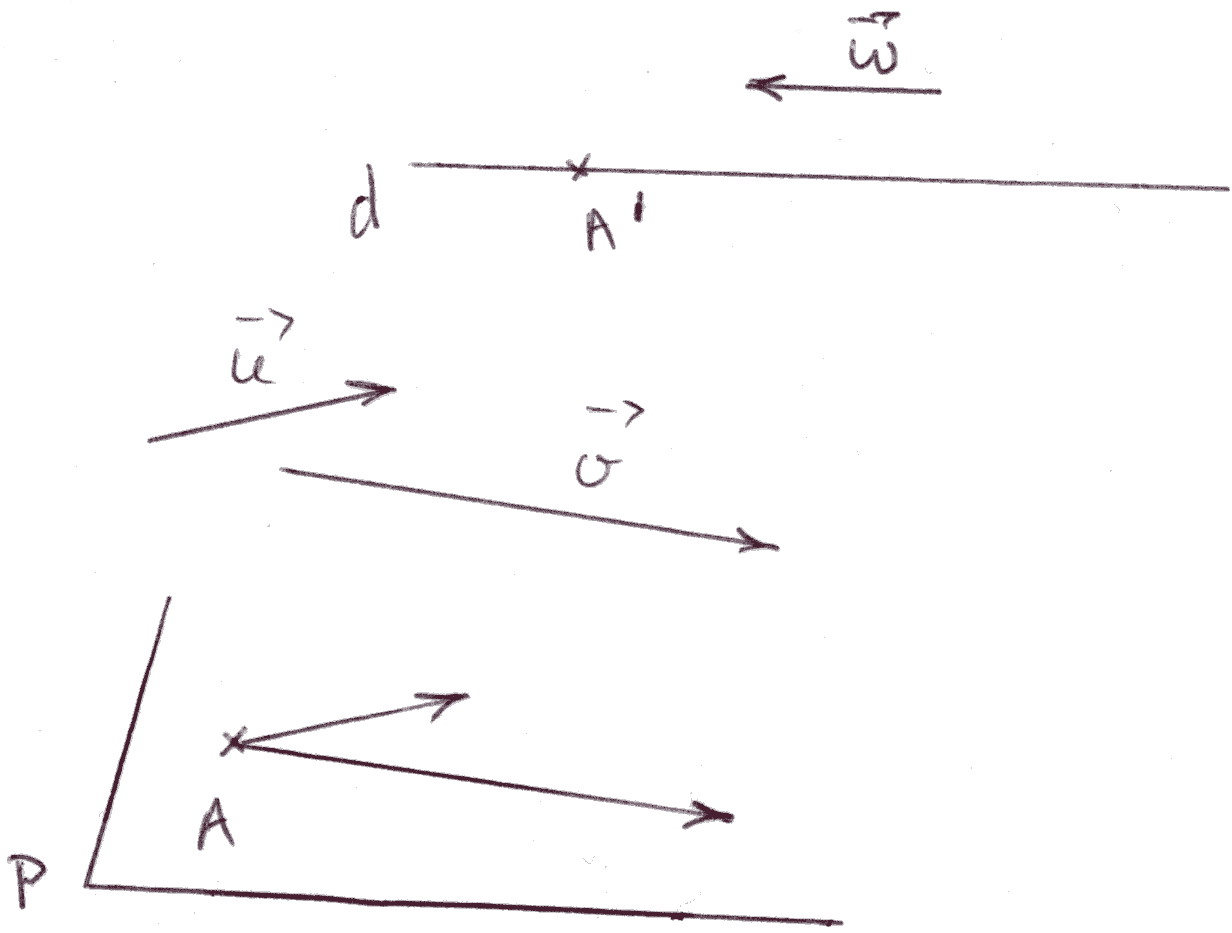
Figure 21
d étant parallèle à P, soit
un plan Q quelconque contenant d et sécant à P ; soit d’
l’intersection de Q et P.
Q contenant d parallèle à P, d’est donc parallèle à d.
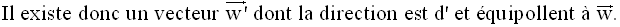
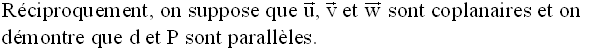

Théorème

(Figure 22)
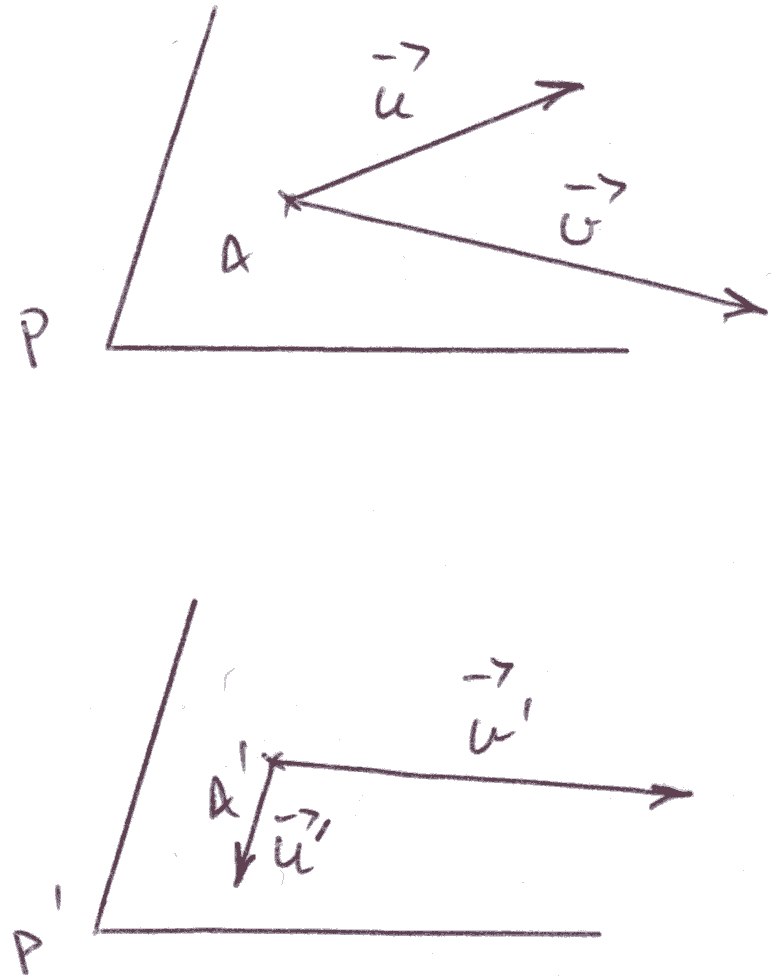
Figure 22
Démonstration
Au début de ce chapitre, on
a établit que deux plans sont parallèles si et seulement si
l’un d’eux contient deux droites concourantes telles que chacune d’elles est
parallèle
à l’autre plan.
On a également établit que
si deux plans sont parallèles, tout plan qui leur est sécant,
les coupera selon deux droites parallèles.
On suppose que P et P’ sont parallèles et on
démontre que :
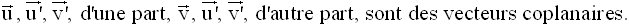


Réciproque
Par hypothèse, on a :
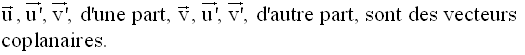
On démontre alors que P et P’ sont parallèles.
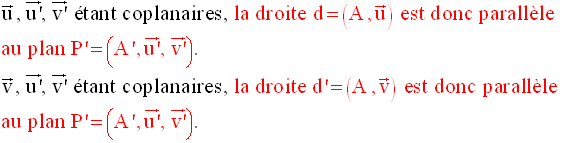
Le plan P,
contenant deux droites concourantes d et d’, chacune d’elles étant parallèles
au plan P’, est donc parallèle au plan P’.
7- Barycentre d’un
système de points de l’espace
7-1 Introduction :
signification de la notion de barycentre d’un système fini de
points de l’espace
Le barycentre d’un système
fini de points de l’espace, affectés de
coefficients réels, est
le modèle mathématique du barycentre d’un système fini de points
matériels, affectés
de masses.
7-2 Définitions

Le point G est appelé barycentre du système de ces n points.
Remarque importante
Le barycentre n’existe que
si la somme des coefficients réels est différente
de zéro.
Cas particulier

Démonstration
Existence du barycentre
Soit O un point quelconque de l’espace.
En appliquant la relation de Chasles, l’égalité vectorielle peut s’écrire :
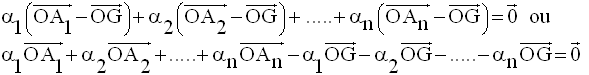
ou

Unicité du barycentre
Supposons que le système admette un second barycentre G’ ; on a donc :

La relation de Chasles permet d’écrire :
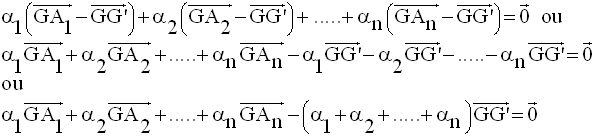
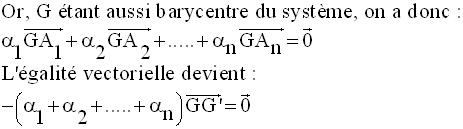
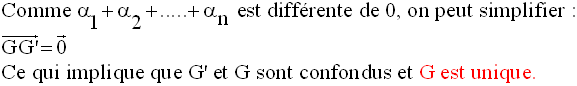
Une deuxième définition du barycentre d’un système fini de points pondérés
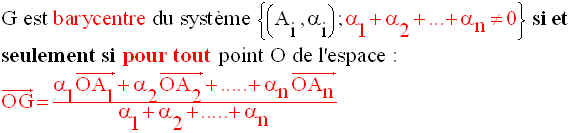
Si l’on fait confondre O avec G, cette dernière égalité vectorielle donne à nouveau :
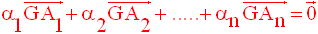
7-3 Propriétés
1ère propriété
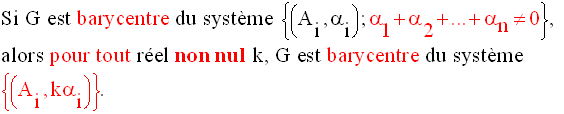
Le barycentre est
inchangé (on dit aussi
invariant) lorsque l’on multiplie les coefficients
par un réel non nul.
2ème propriété
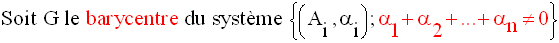
Si l’on peut extraire de ce système un sous système défini comme suit :
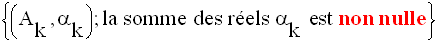
alors ce sous système admet un barycentre g.
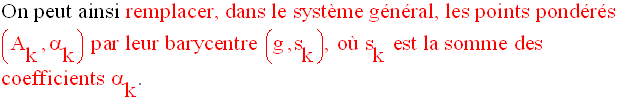
C’est ce qu’on appelle l’associativité du barycentre.
A titre d’exercice, démontre cette propriété pour le système :
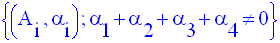
sachant que l’on a :
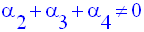
Exercices
1)
On donne un tétraèdre (ABCD).
On désigne par
M, N, P, Q, R et S, les milieux respectifs des arêtes [AB], [AC], [AD],
[BC], [CD] et [BD].

a- Montre que le quadrilatère (MNRS) est un parallélogramme.
b- En déduire que les droites (MR), (NS) et (PQ) sont concourantes.
Solution
a-
Dans le plan (ABC), M et N
étant respectivement milieux des côtés [AB] et [AC]
du triangle (ABC), on a :
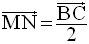
Dans le plan (BCD), R et S
étant respectivement milieux des côtés [CD] et [BD] du
triangle (BCD), on a :
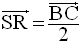
Par conséquent,
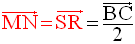
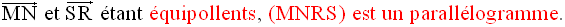
b-
(MNRS) étant un
parallélogramme, ses diagonales [MR] et [NS] concourent en leur
milieu O.
Dans le plan (ABC), M et Q
étant respectivement milieux des côtés [AB] et [BC]
du triangle (ABC), on a :
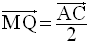
Dans le plan (ACD), P et R
étant respectivement milieux des côtés [AD] et [DC] du
triangle (ACD), on a :
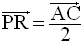
Par conséquent,
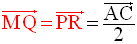
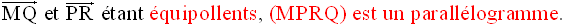
(MPRQ) étant un
parallélogramme, ses diagonales [MR] et [PQ] concourent en leur
milieu.
Or, le milieu de [MR], diagonale du parallélogramme (MNRS), est O.
Par conséquent, O appartient
à [PQ] et les droites (MR), (NS) et (PQ) concourent au
point O.
2)
On donne un parallélépipède oblique (ABCDA’B’C’D’) ;
On a :
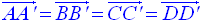
Soient M, N, O, P, Q et R les centres des faces respectives (ABCD), (A’B’C’D’), (ADD’A’), (BCC’B’), (ABB’A’) et (DCC’D’).
1° Montre que le quadrilatère (MONP) est un parallélogramme.
2° En déduire que les droites (MN), (OP) et (QR) sont concourantes.
Solution
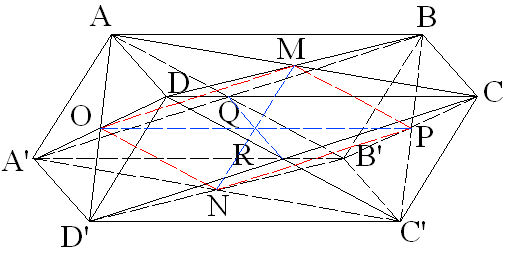
1°
Dans le plan (A’DB), O et M
étant milieux respectifs des côtés [A’D] et [DB] du triangle
(A’DB), on a :
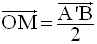
Dans le plan (B’D’C), N et P étant milieux respectifs des côtés [B’D’] et [B’C] du triangle (B’D’C), on a :
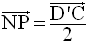
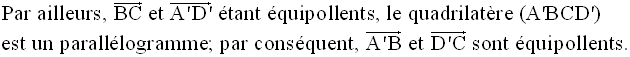
On en déduit :

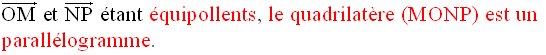
2°
(MONP) étant un
parallélogramme, ses diagonales [MN] et [OP] concourent en leur
milieu.
Dans le plan (A’DB), Q et M
étant milieux respectifs des côtés [A’B] et [DB] du
triangle (A’DB), on a :
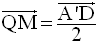
Dans le plan (B’D’C), N et R
étant milieux respectifs des côtés [D’B’] et [D’C] du
triangle (B’D’C), on a :
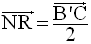
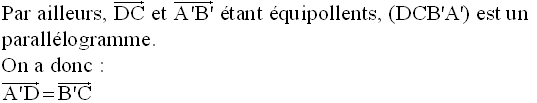
Par conséquent,
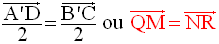

Par conséquent, les droites (MN), (OP) et (QR) sont concourantes.
3)
On donne un tétraèdre (ABCD).
On définit les points E et F par les égalités vectorielles :
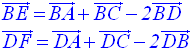
Démontre que les plans (BCD) et (AEF) sont parallèles.
Solution

Construction des points E et F
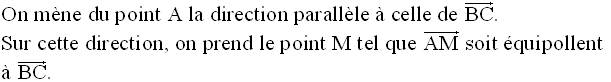
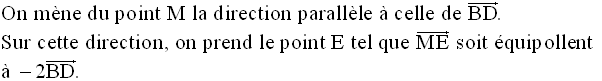
On a donc :
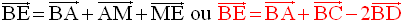
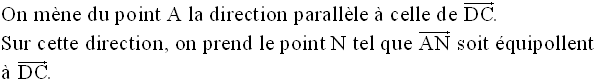
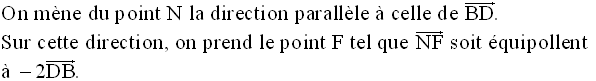
On a donc :
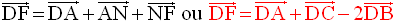
On démontre ensuite que les plans (BCD) et (AEF) sont parallèles.


La relation de Chasles appliquée à l’égalité vectorielle :
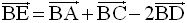
donne :
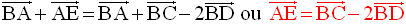

La relation de Chasles appliquée à l’égalité vectorielle :
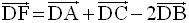
donne :
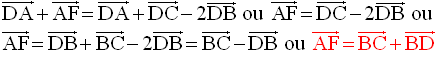
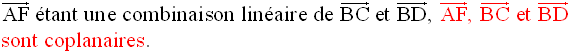


Ces deux dernières équations étant incompatibles, il n’existe donc pas un réel k tel que :
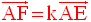
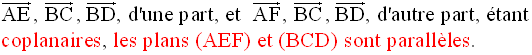
4)
On donne un tétraèdre (ABCD).
On donne également les points E et F définis comme suit :
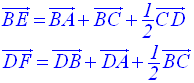
Démontre que les plans (BCD) et (AEF) sont parallèles.
(Tu démontreras que les points A, E et F ne sont pas alignés)
Solution
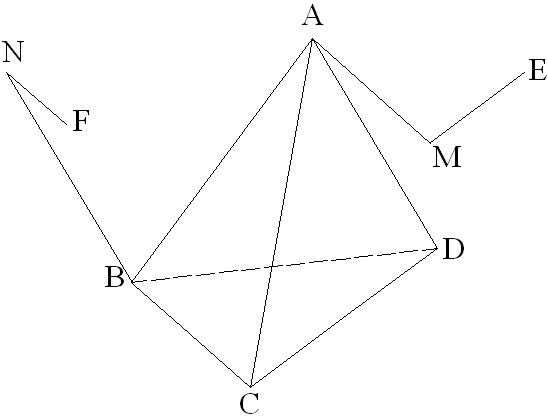
Construction des points E et F
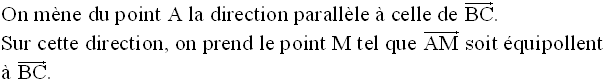

On a donc :
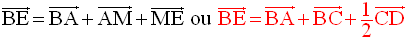
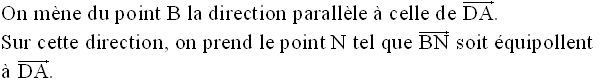
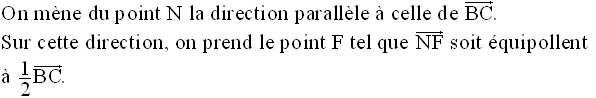
On a donc :
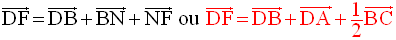
On démontre ensuite que les plans (BCD) et (AEF) sont parallèles.


La relation de Chasles appliquée à l’égalité vectorielle :
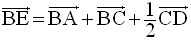
donne :
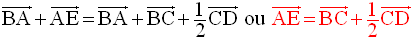
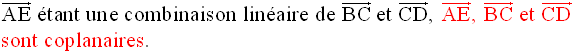
La relation de Chasles appliquée à l’égalité vectorielle :
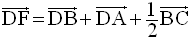
donne :
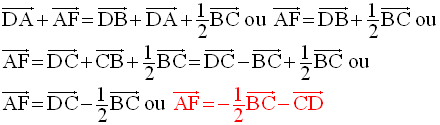
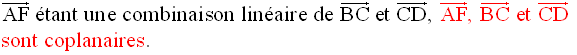
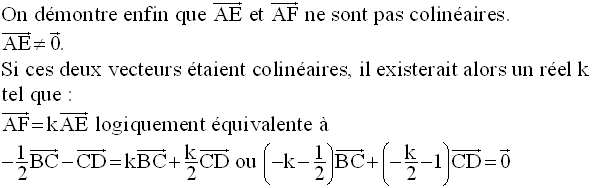

Ces deux dernières équations étant incompatibles, il n’existe donc pas un réel k tel que :
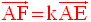
Le plan (AEF) est donc défini.
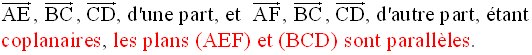
5)
On donne un tétraèdre (ABCD).
Soit E l’image de B dans la symétrie centrale de centre C.
Soit F l’image de B dans la symétrie centrale de centre D.
Les points I et J sont les milieux respectifs des arêtes [AB] et [CD].
Démontre que la droite (IJ) est parallèle au plan (AEF).
Solution
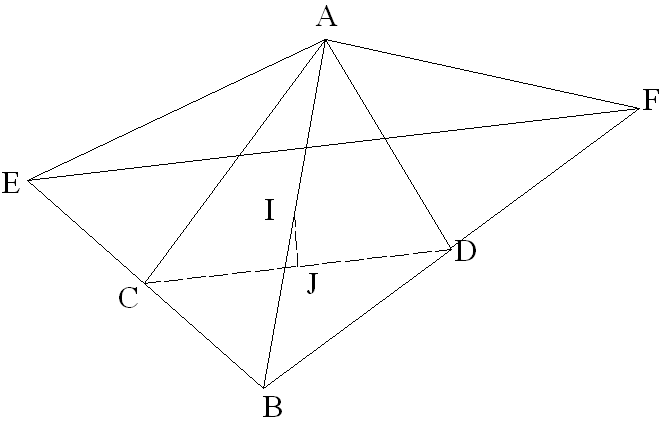

La relation de Chasles permet d’écrire :
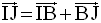
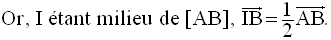
L’égalité vectorielle s’écrit alors :
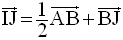
Comme J est le milieu de [CD], on a :
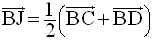
Par ailleurs, C et D étant les milieux respectifs de [EB] et [BF], on a :
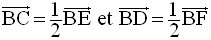
D’où
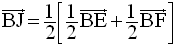
Par conséquent, on a :
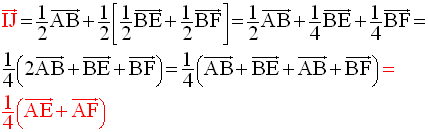

6)
On donne un tétraèdre (ABCD).
a- Construis les points E, E’, F et F’ définis par les relations vectorielles suivantes :
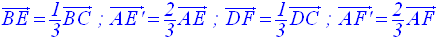
b- Démontre
que les droites (BD) et (E’F’) sont parallèles en prouvant la colinéarité
des vecteurs :
Je te laisse résoudre cet exercice.
7)
Soit un tétraèdre (ABCD).
a- Construis les points I, E, F et G définis comme suit :
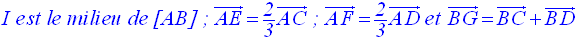
b- Démontre que les points I, E, F et G sont coplanaires.
c- Soit H le milieu de [BI]. Démontre que les plans (IEF) et (HCD) sont parallèles.
Solution
a-
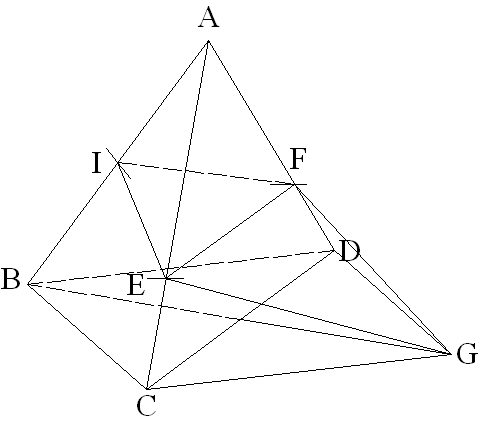
Je te laisse faire la construction des points I, E, F et G.
b-
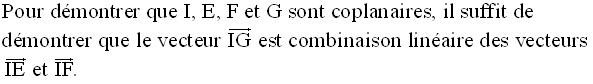
La relation de Chasles permet d’écrire :

I étant milieu de [AB], on a :
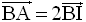
D’où
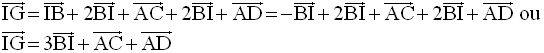
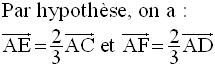
On en tire :
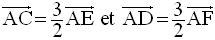
D’où
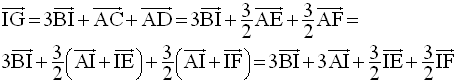
I étant milieu de [AB], on a :
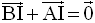
On en déduit :
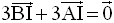
D’où
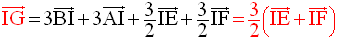

c-
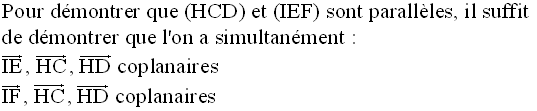
La relation de Chasles permet d’écrire :
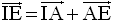
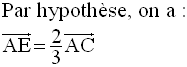
Par ailleurs, à l’aide de la relation de Chasles, on a :
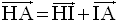
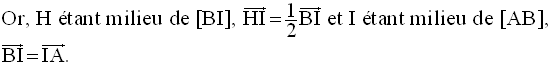
On en tire :
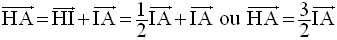
D’où
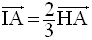
Par conséquent, on obtient :
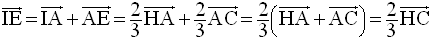
Cette dernière égalité vectorielle peut donc s’écrire :


La relation de Chasles permet d’écrire :
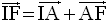
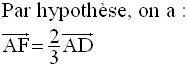
Or, plus haut on a démontré que :

D’où
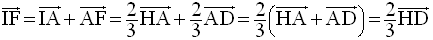
Cette dernière égalité vectorielle peut donc s’écrire :
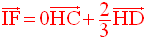

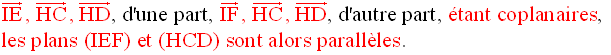
8)
Construction du barycentre d’un système de points
La méthode générale
Pour construire le barycentre d’un système de points pondérés de l’espace, on doit :
a- écrire la relation vectorielle définissant le barycentre considéré ;
b-
transformer
cette relation vectorielle afin d’obtenir un vecteur dont
une des
extrémités est le barycentre,
en fonction de vecteurs fixes
connus ;
c- construire le barycentre en utilisant la relation vectorielle transformée à l’étape b.
8-1
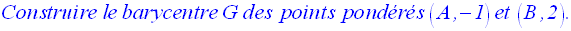
8-2
A, B et C sont les sommets d’un triangle.

8-3
On donne un quadrilatère (ABCD).
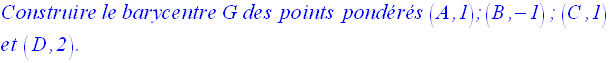
Solution
8-1
On vérifie d’abord si la
somme des coefficients est différente de zéro, sinon le barycentre
n’existe pas.
On a :
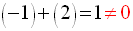
Donc, le barycentre G à construire existe.
La relation vectorielle définissant G est :
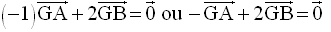
On transforme cette relation à l’aide de la relation de Chasles ; on obtient :
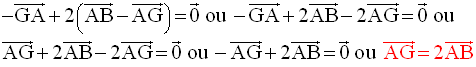
Cette dernière égalité
vectorielle implique que G appartient à la droite (AB) et que
l’on a :
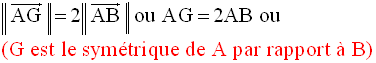
Avec ces conclusions, il devient facile de construire G.
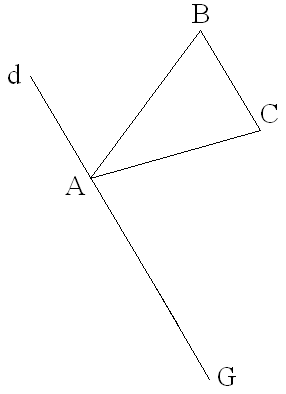
8-2
On vérifie d’abord si la somme des coefficients est différente de zéro.
On a :
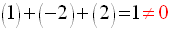
Donc, le barycentre G à construire existe.
La relation vectorielle définissant G est :
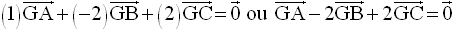
On transforme cette relation à l’aide de la relation de Chasles ; on obtient :
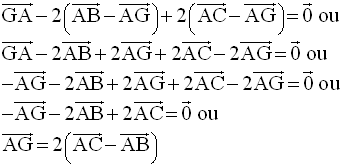
D’après la relation de Chasles, on a :
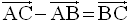
Finalement, on obtient :
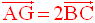

On obtient la figure suivante :
8-3
Je te laisse résoudre cette partie.
Tu dois trouver comme résultat, la relation vectorielle :
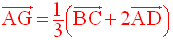
9)
Comment reconnaître un barycentre ?
La méthode générale
On doit, au départ, avoir une relation vectorielle entre tous les points donnés.
A l’aide des
outils du calcul vectoriel, on transforme cette relation vectorielle afin
qu’elle prenne la forme de celle
ayant servie à la définition du barycentre.
Ayant obtenu
cette forme, on s’assure que
la somme de ses coefficients réels est
différente de zéro.
9-1
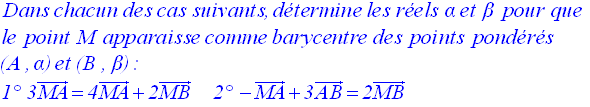
9-2
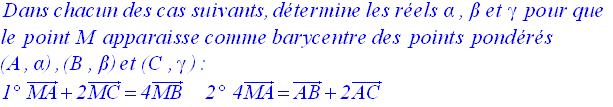
9-3
On donne quatre points A, B, C et D.
Soit le point M tel que :
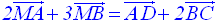
Démontre que M
est le barycentre des quatre points donnés affectés de coefficients
à déterminer.
Solution
9-1
1°
On transforme la relation
vectorielle donnée pour la mettre sous la forme de celle
ayant servi à définir le barycentre ; on a :
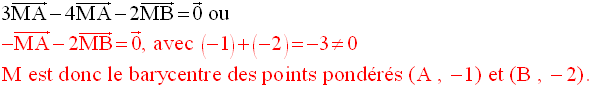
2°
Je te laisse faire cette partie ; tu dois trouver comme résultat :

9-2
Je te laisse faire cette partie ; tu dois trouver comme résultat :
1°

2°
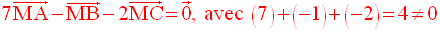
9-3
On transforme la relation
vectorielle donnée pour la mettre sous la forme de celle ayant
servi à définir le barycentre, ceci en utilisant la relation de Chasles, dans le
second
membre de la relation donnée ; on a :

10)
On donne dans l’espace un tétraèdre (ABCD).
Soient I et J les milieux respectifs des arêtes [AC] et [BD].
Soit G le barycentre des points pondérés (A,1), (B,2), (C,1) et (D,2).
1° Soient M le
barycentre de (A,1) et (B,2) et N celui de (C,1) et (D,2).
Démontre que G est milieu de [MN] et construis G.
2° Démontre
que les points I, J et G sont alignés et précise la position de G à
l’aide d’une relation vectorielle.
Solution
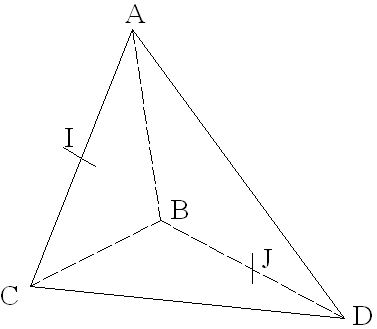
1°
G étant le barycentre des points pondérés (A,1), (B,2), (C,1) et (D,2), on a :
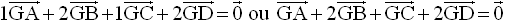
M étant le barycentre de (A,1) et (B,2) et N celui de (C,1) et (D,2), on a :
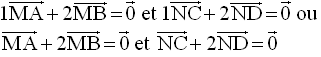
La propriété d’associativité du barycentre permet de grouper les points (A,1) et (B,2) en les remplaçant par leur barycentre M affecté du coefficient :
La même propriété permet de
grouper les points (C,1) et (D,2) en les remplaçant par
leur barycentre N affecté du coefficient :
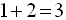
La relation vectorielle ayant permis de définir G devient alors :
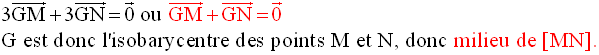
Construction de G
Les relations suivantes permettent de construire M et N :
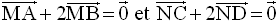
On a :
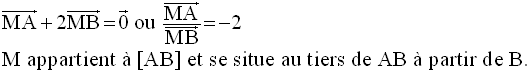

Après avoir positionné M et N, on construit le point G, milieu de [MN].
On obtient la figure suivante :
2°
On utilise l’associativité
du barycentre, en groupant, d’une part les points pondérés
(A , 1) et (C , 1), et d’autre part les points pondérés (B , 2) et (D , 2).
Le barycentre des points
pondérés (A , 1) et (C , 1) est le milieu I de [AC] ; celui des
points pondérés (B , 2) et (D , 2) est le milieu J de [BD].
Le point G est donc le
barycentre des points pondérés (I , 1 + 1) ou (I , 2) et (J , 2 + 2)
ou (J , 4) ; on obtient donc la relation vectorielle :
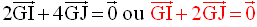
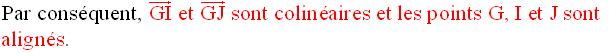
G appartient donc à [IJ] et se situe aux deux tiers de IJ comptés à partir de I.
11)
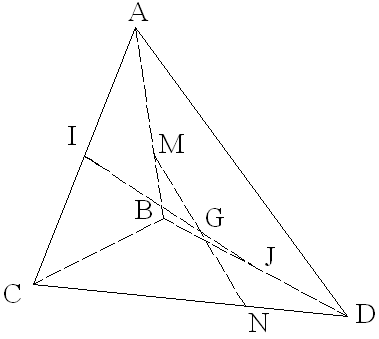
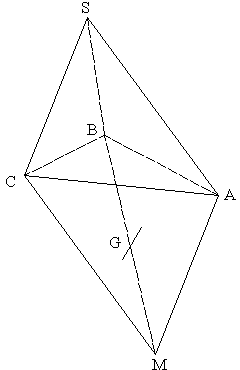
Soit (SABC) un tétraèdre de l’espace.
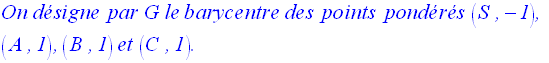
1°
a)
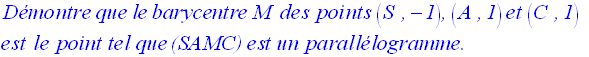
b)
Démontre que G est le milieu de [BM].
2°
Soient N et P
les points tels que (SANB) et (SBPC) sont des parallélogrammes.
Démontre que G est le milieu de [CN] et de [AP].
3°
Soit K le
centre de gravité du triangle (ABC). Démontre que les points S, K et G sont
alignés.
Solution
1°
a)

b)
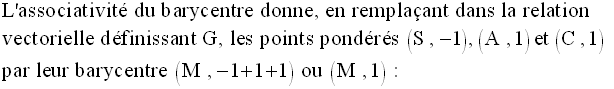
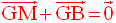
Par conséquent G est milieu de [BM].
2°
(SANB) étant un parallélogramme, on a :
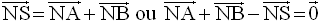
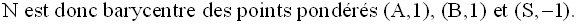
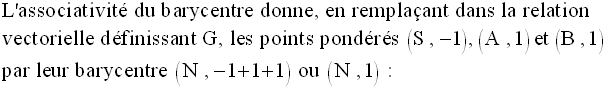
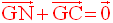
Par conséquent G est milieu de [CN].
(SBPC) étant un parallélogramme, on a :
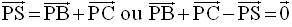
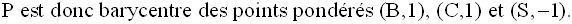
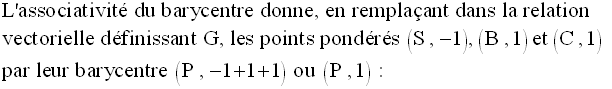

Par conséquent G est milieu de [AP].
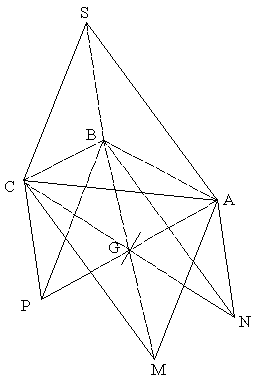
3°
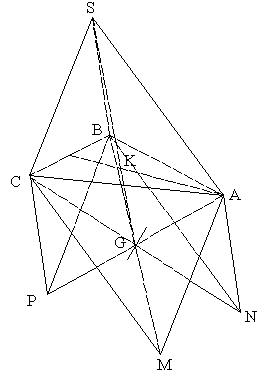
K étant le centre de gravité du triangle (ABC), on a :
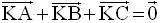
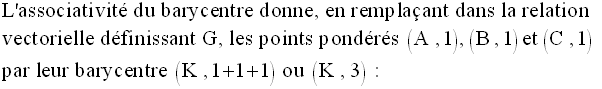
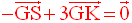
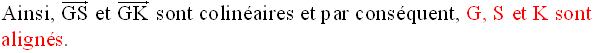
12)
Dans le plan, on donne le triangle (ABC).
Soit M le milieu de [AC] et soient les points N et P définis comme suit :
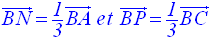
1°
Ecris M comme
barycentre de A et C, puis N comme barycentre de A et B et
enfin P comme barycentre de B et C.
2°
Démontre que les droites (MB), (NC) et (PA) sont concourantes.
Solution
1°
M étant milieu de [AC], on a :
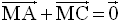
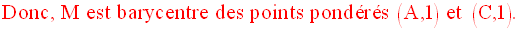
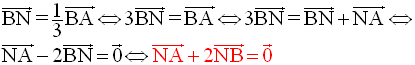
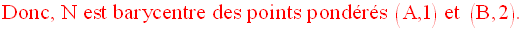


2°
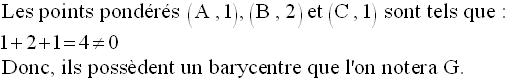
Ainsi, on a :

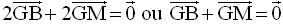

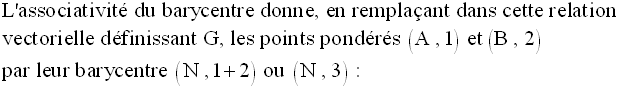

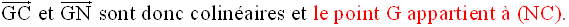

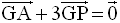
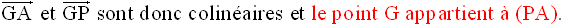
G appartenant simultanément à (PA), (NC) et (MB), ces droites sont donc
concourantes.
Je te laisse le soin de résoudre les deux derniers exercices qui suivent :
13)
On donne dans le plan un quadrilatère quelconque (ABCD).
Soit G le barycentre des points pondérés (A,1), (B,2), (C,1) et (D,2).
1°
Construis le
barycentre K des points pondérés (A,1) et (B,2), ainsi que le barycentre L
des points (C,1) et (D,2).
2°
Pour tout point M du plan, justifie l’égalité vectorielle :
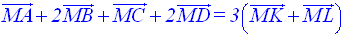
3°
En déduire que g est l’isobarycentre des points K et L et construis G.
4°
Construis le
barycentre K’ des points pondérés (A,1) et (D,2), ainsi que le barycentre
L’ des points pondérés (C,1) et (B,2).
5°
Démontre que G est l’isobarycentre des points K’ et L’.
6°
Quelle est la nature du quadrilatère (KK’LL’) ?
7°
Soient I et J
les milieux respectifs de [AC] et [BD]. Démontre que I, G et J sont
alignés et exprime G comme barycentre des points I et J, les coefficients étant
à préciser.
14)
On donne dans
l’espace un tétraèdre (ABCD) et on désigne par G l’isobarycentre
des sommets.
1°
Démontre que G
est le milieu de chacun des segments dont les extrémités sont les
milieux de deux arêtes opposées.
2°
On désigne
respectivement par A’, B’, C’ et D’ les centres de gravité des triangles
(BCD), (ACD), (ABD) et (ABC).
a- Démontre que G appartient aux droites (AA’), (BB’) (CC’) et (DD’).

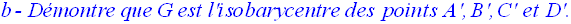
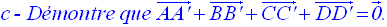
fonctions
numériques dérivables en un point
(groupes ciblés : première et
terminale S)
Rappel de cours
1-
Limite à gauche et limite à droite d’une fonction numérique
Soit
un réel fini fixé x0 .
On
dira que la variable réelle x tend vers x0 par valeurs inférieures
et on écrit :
![]()
lorsque x tend vers x0 en
restant strictement inférieure à x0 .
On
dira que la variable réelle x tend vers x0 par valeurs supérieures
et on écrit :
![]()
lorsque x tend vers x0 en restant strictement
supérieure à x0 .
Soit une fonction numérique f définie au point x0 .
Par définition, la limite à gauche de la fonction f lorsque x tend vers
x0 par valeurs inférieures est le réel l tel que :
![]()
La limite à droite de la fonction f lorsque x tend vers x0
par valeurs supérieures est le réel l’ tel que :
![]()
On dira que f est continue au point x0 lorsque l = l’ = f (x0).
2-
Fonction dérivable en un point et dérivée
Soit
une fonction numérique f définie au point x0 .
On dira que f est dérivable à gauche au point x0
si et seulement si :
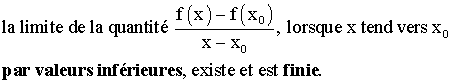
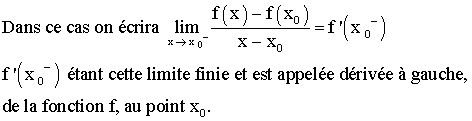
On
dira que f est dérivable à droite au point x0
si et seulement si :
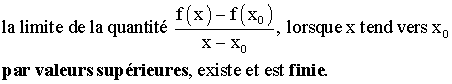
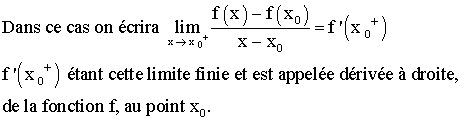
La
fonction f est dérivable au point x0
si et seulement si elle est dérivable à gauche et à
droite au point x0 et ses deux dérivées sont égales.
Ceci
signifie que l’on a :
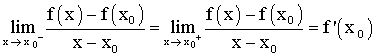
![]()
3-
Remarques
3-1

Ainsi
f est dérivable au point x0 si et seulement si :
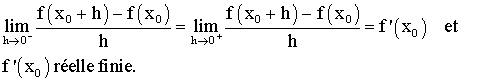
Ainsi
utiliser l’une ou l’autre expression dans la recherche de la dérivée
revient au même.
3-2
Si
f est dérivable au point x0 , alors f est continue en ce point ;
mais la réciproque n’est pas vraie.
Ainsi
pour démontrer qu’une fonction numérique est continue en un point, il
suffit de démontrer qu’elle est dérivable en ce point ; cet énoncé
est souvent utile dans les problèmes.
Mais attention, la réciproque n’est pas vraie : une fonction peut être continue en un point sans pour autant être dérivable en ce même point.
Applications
1)
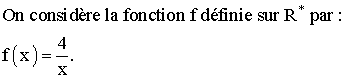
Montrer
que f est dérivable en 2 et calculer f '(2).
2)
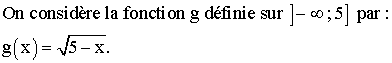
Montrer
que g est dérivable en 1 et calculer g '(1).
3)

Montrer que u
est dérivable en -3 et calculer u '(-3).
Solutions
1)
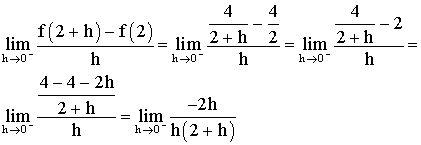
Mais h tendant vers 0 reste donc différent de 0 et on peut simplifier par h et ainsi :
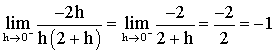
f
est donc dérivable à gauche au point 2.
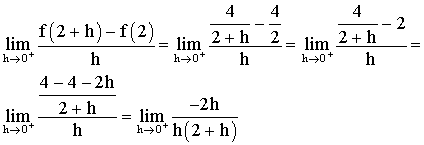
Mais h tendant vers 0 reste donc différent de 0 et on peut simplifier par h et ainsi :

f
est donc dérivable à droite au point 2.
De
plus ces deux limites sont égales à -1.
Conclusion : f est dérivable au point 2 et sa valeur est f ’(2) = -1 .
2)
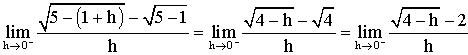
Lorsque
h tend vers 0 cette fraction prend la forme indéterminée :
![]()
Pour lever l’indétermination, multiplions le numérateur et le dénominateur par le conjugué du numérateur; il vient :

Mais
h tendant vers 0, reste différent de 0 et on peut simplifier par h :
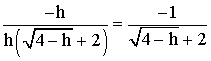
Ainsi,
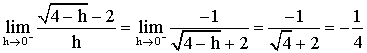
Conclusion : g est dérivable à gauche au point 1.
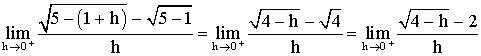
Lorsque
h tend vers 0 cette fraction prend la forme indéterminée :
![]()
Pour lever l’indétermination, multiplions le numérateur et le dénominateur par le conjugué du numérateur; il vient :
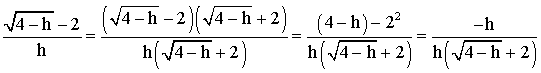
Mais
h tendant vers 0, reste différent de 0 et on peut simplifier par h :
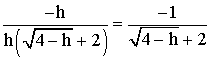
Ainsi,

Conclusion :
g est dérivable à droite au point 1.
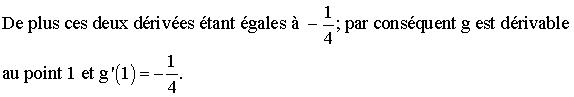
3)
Je
te laisse montrer que u est dérivable au point -3.
Tu dois trouver u’(-3)=135.
Autres applications
a-
Montre
que la fonction w définie sur R par :
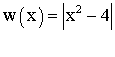
Tu dois trouver les résultats suivants :
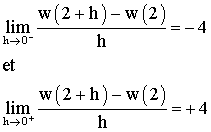
b-
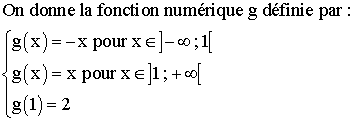
g
est-elle continue au point 1 ?
g
est-elle dérivable au point 1 ?
Trace
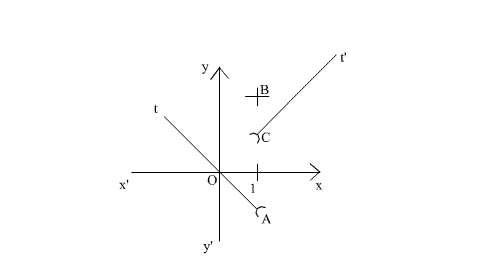
dans un repère orthonormal la courbe représentative Cg de g.
Tu
dois trouver comme résultats :
g
n’est ni continue, ni dérivable au point 1.
Construction de Cg :
c-
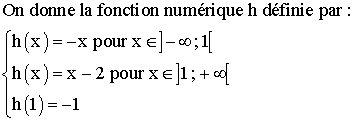
h
est-elle continue au point 1 ?
h
est-elle dérivable au point 1 ?
Trace
dans un repère orthonormé la courbe représentative Ch de h.
Tu dois trouver comme résultat :
h
est continue et non dérivable au point 1
Quant
à Ch, je te laisse la tracer.
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)